Physics DSM: Chapter 12: Rotation of a Rigid Body

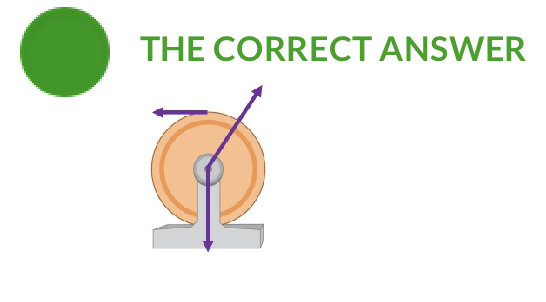
The correct free-body diagram shows three forces: The rope pulls left at the top point of the pulley, the force of earth’s gravity pulls down at the center of the pulley, and the axle must push both up and to the right in order to cancel out the first two forces (since the translational acceleration of the pulley is zero). Note only the rope produces a nonzero torque about the center of mass, which is why the pulley starts rotating (even thought the net force on it is zero).

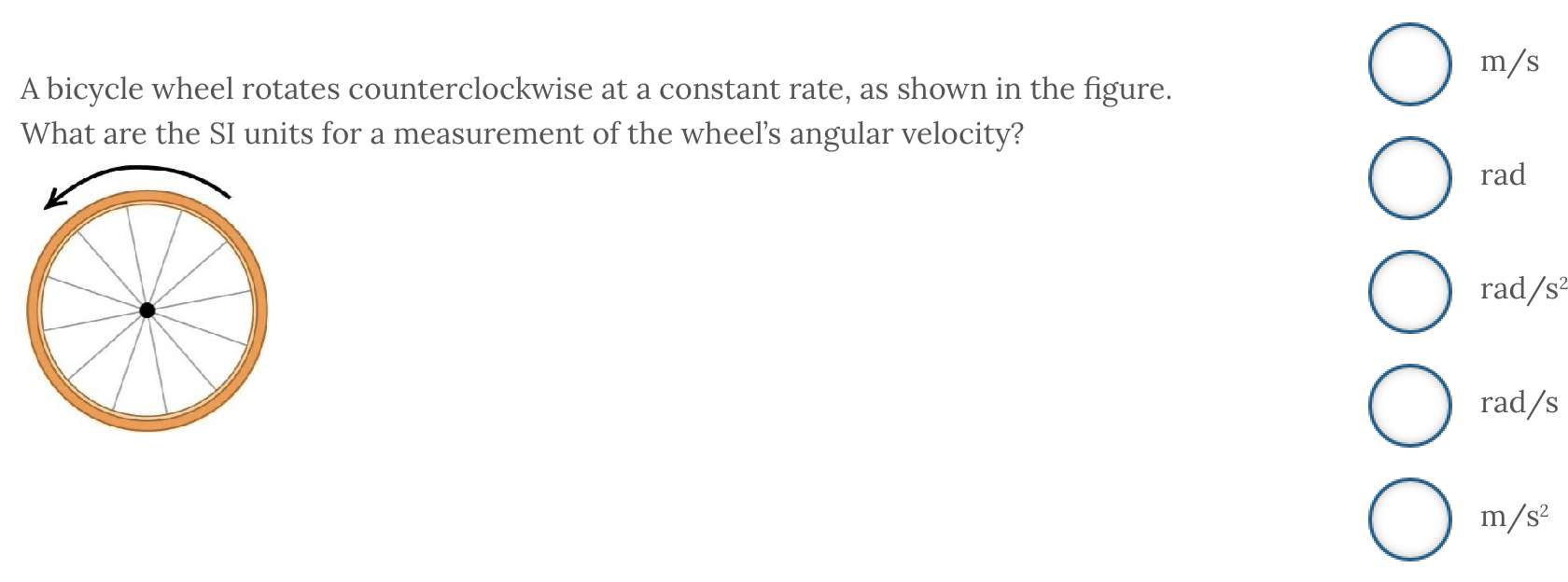
ANSWER: rad/s

EXPLANATION: The wheel’s angular velocity is measured with SI units of rad/s. The angular velocity is a measurement of how the angular position, 𝑤⃗ = Δθ / Δt.

 

Radians (rad) are the units for an angular displacement but not how that angle changes in time.

 

The SI units of m/s are appropriate for a rate of change in position, but that is a translational position and not an angular position.

 

The SI units of rad/s² are used for angular acceleration (𝛼⃗), not angular velocity (𝛼⃗).

 

The SI units of m/s² are what we use for translational acceleration.  

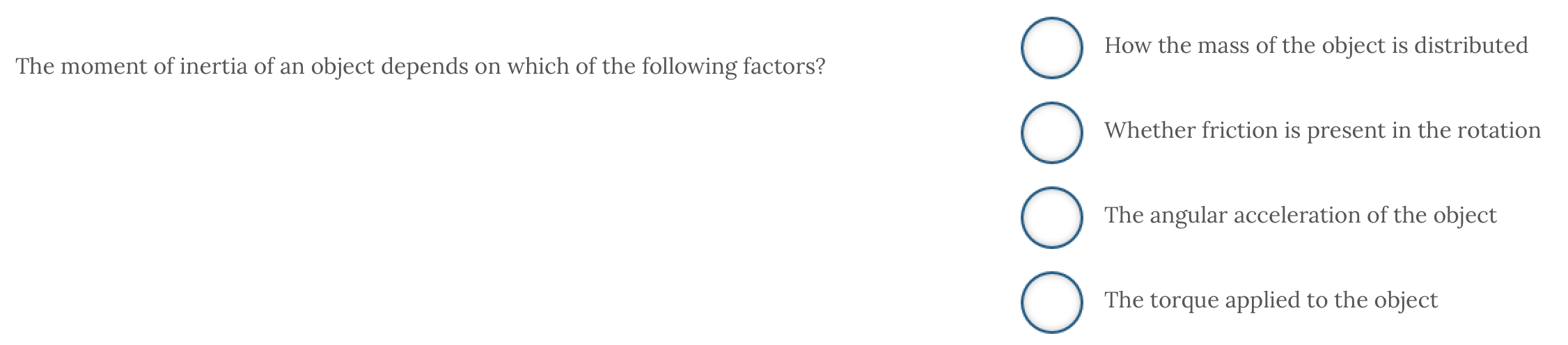
ANSWER: How the mass of the object is distributed

ANSWER: can change its own angular velocity by rearranging its mass distribution

EXPLANATION: Without external torques an object can change its own angular velocity by rearranging its mass distribution. External torques are required in order for an object to change its angular momentum, but even while the angular momentum stays constant an object can change its angular velocity by shifting how its own mass is distributed. A classic example is when an ice-skater spins faster as they bring their limbs in closer to the axis of rotation.

The angular momentum of the object cannot be changed unless external torques are exerted on it, per Newton’s second law for rotating systems.

Velocity cannot be changed except by external forces, per Newton’s second law for translational motion.

ANSWER: rad/s²

ANSWER: Choice C

The location where the force is applied and the force applied by A on B (both magnitude and direction)

ANSWER: I_A = 4I_B

ANSWER: Applying the force at either location A or B will produce the same amount of torque.

ANSWER: The tangential acceleration of point P is less than the tangential acceleration of point Q.

ANSWER: Yes, by exerting her force farther from the gate’s hinge than her father does.

ANSWER: The tangential speed of the rim of the wheel relative to the wheel’s axle is equal to the speed of the wheel’s axle relative to the ground.

EXPLANATION:

•Rolling Without Slipping: The tangential speed of the rim relative to the axle is equal to the speed of the axle relative to the ground.

•Contact Point: The point on the wheel in contact with the ground is at rest.

•Motion Relationship: The rotational motion of the rim cancels out the translational motion of the wheel.

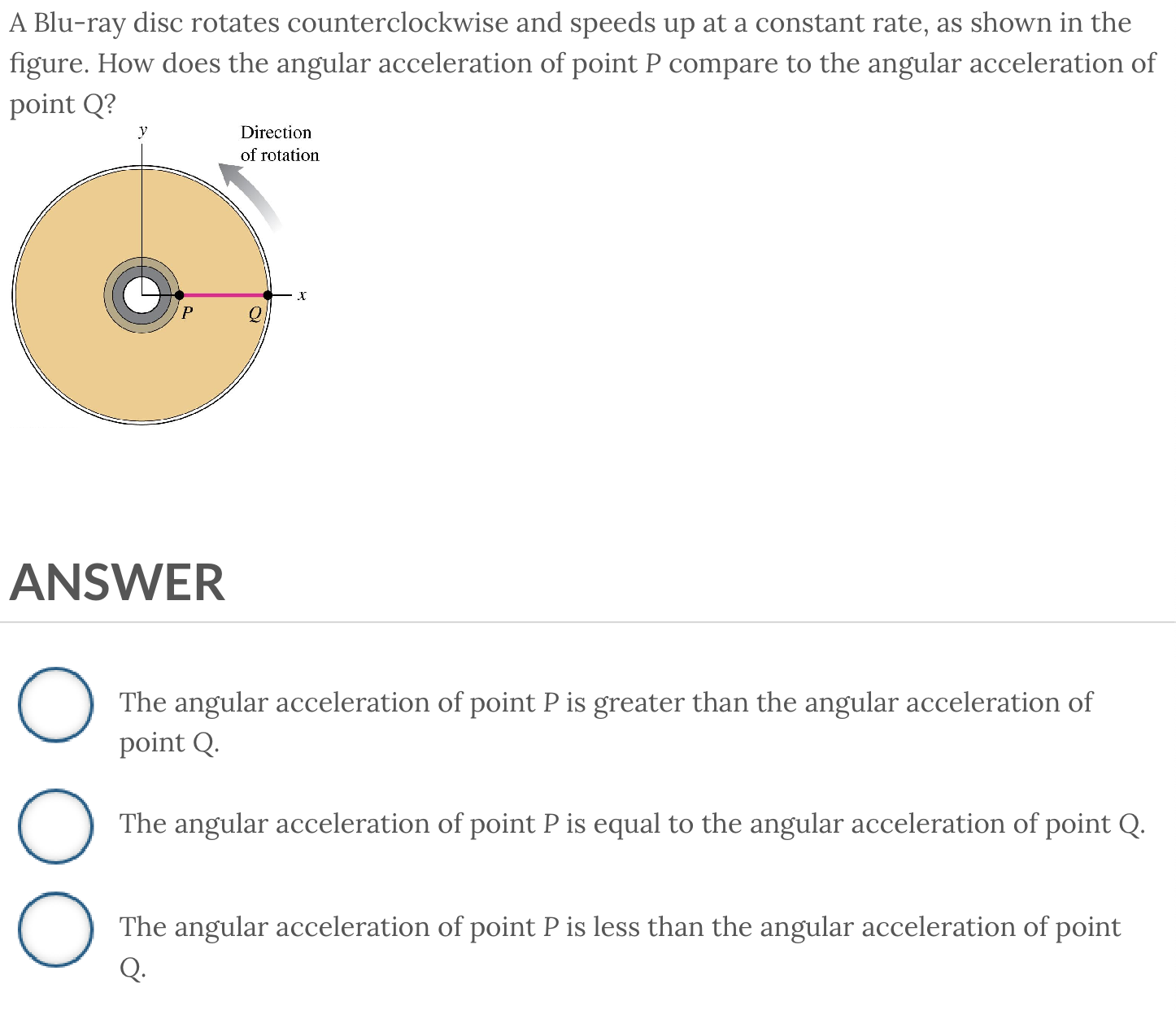
ANSWER: The angular acceleration of point P is equal to the angular acceleration of point Q.

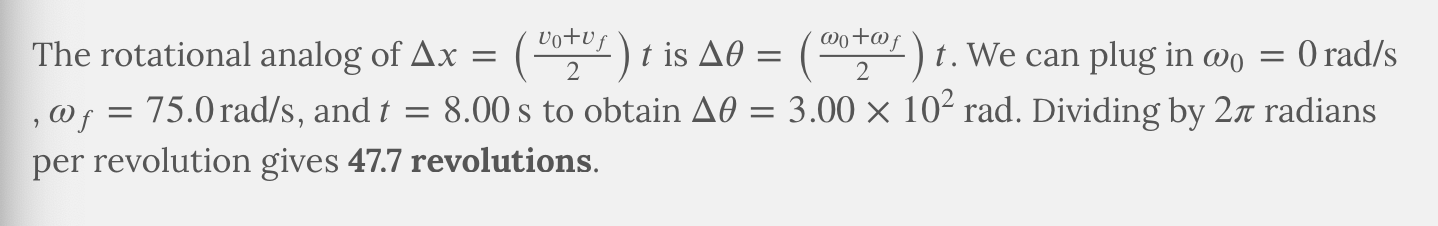
ANSWER: 47.7 revolutions

ANSWER: The speed increases.
EXPLANATION:

•Angular Momentum Conservation: The block’s angular momentum remains constant because the tension force is parallel to the radius of motion and doesn’t exert a net torque.

•Speed Increase: As the radius of the block’s circular path decreases, its speed increases to maintain constant angular momentum.

•Force Explanation: Pulling downward on the string increases the block’s speed, but the tension force doesn’t affect the block’s angular momentum.

ANSWER: x = 44.4 cm

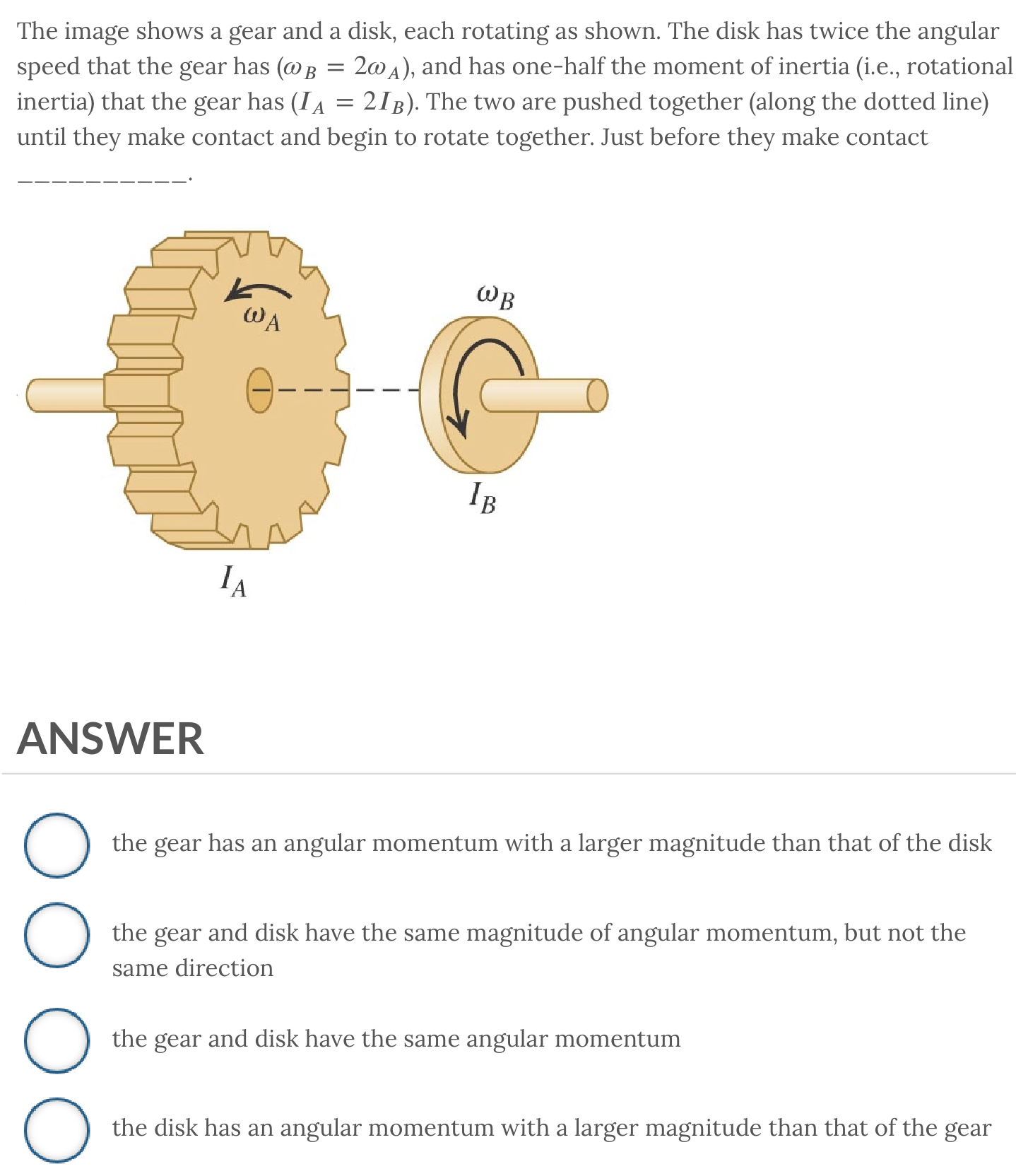
ANSWER: the gear and disk have the same angular momentum

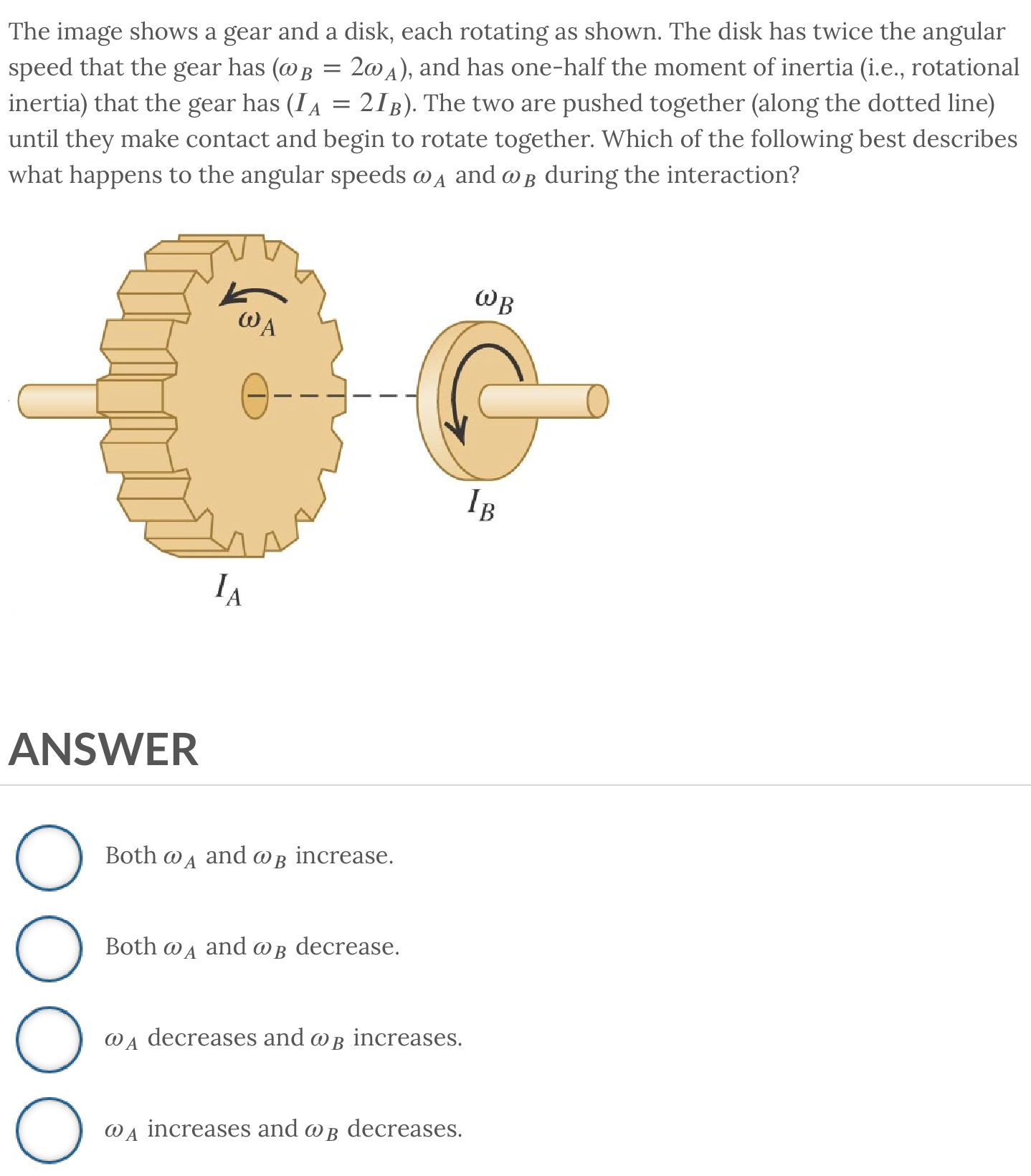
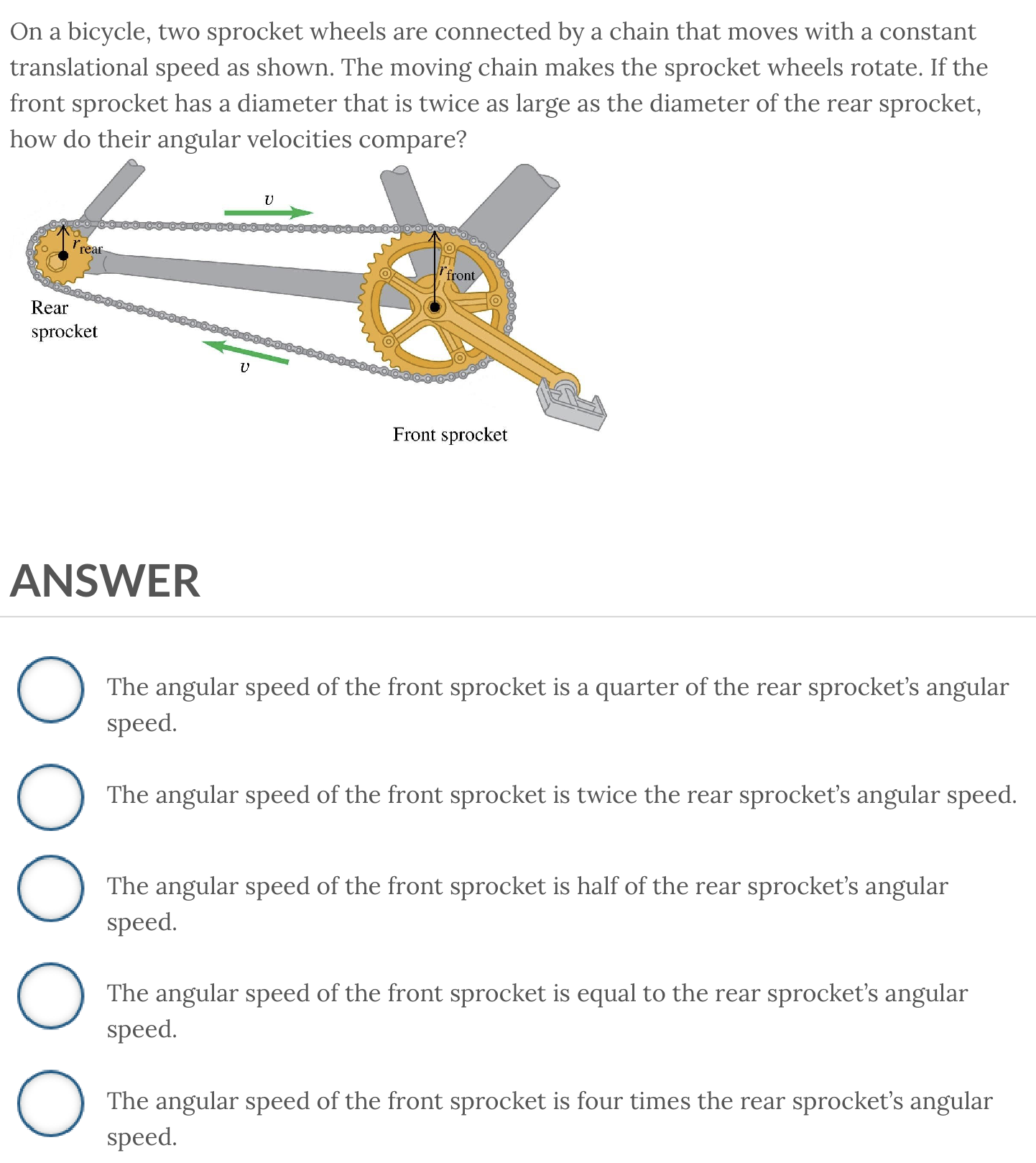
ANSWER: The angular speed of the front sprocket is half of the rear sprocket’s angular speed.

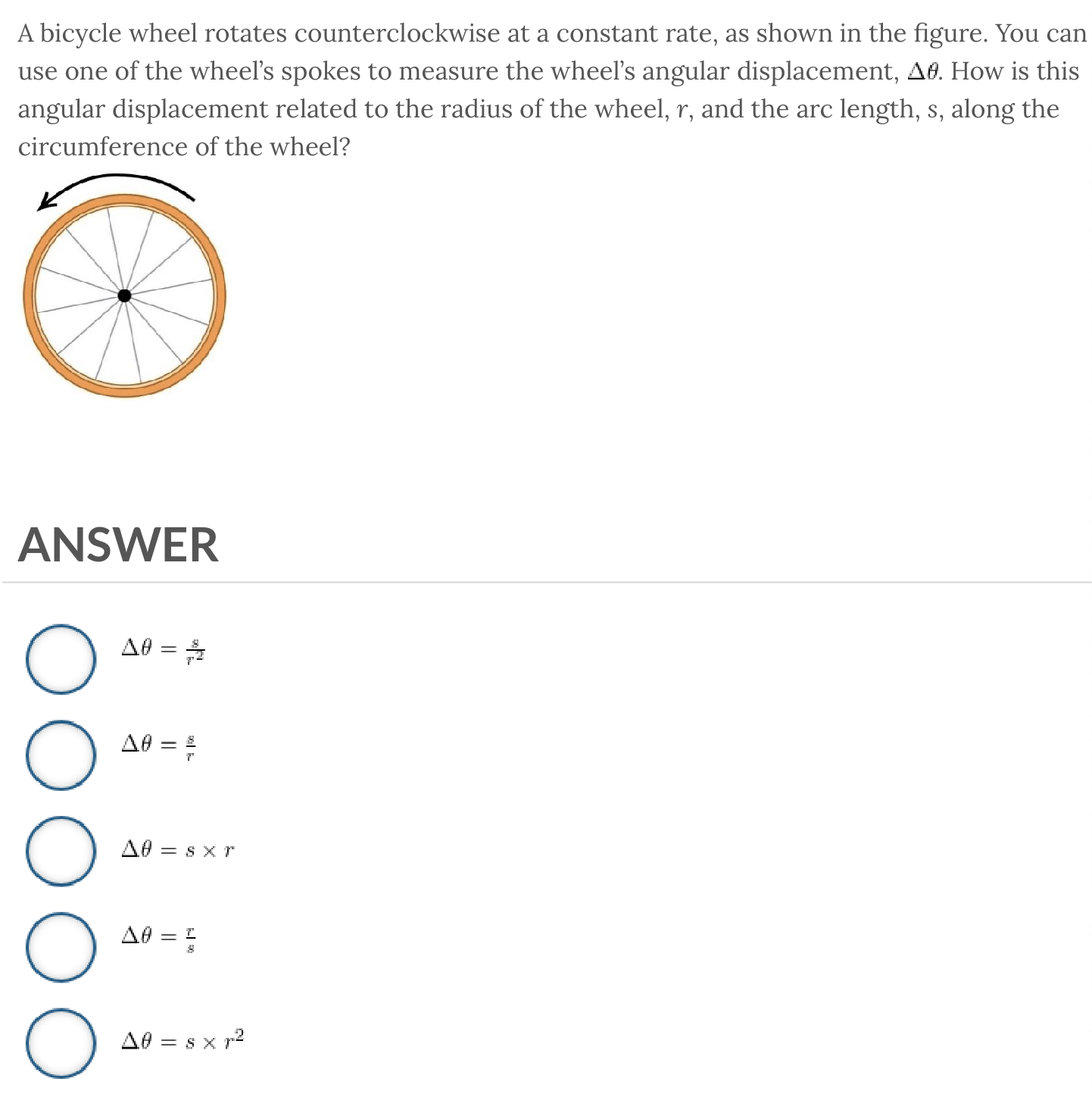
ANSWER: (delta)0 = s / r

ANSWER: Yes, since the external forces (gravity and forces from the axle) do not cause any torque around the axle of the turntable, the angular momentum of the system is conserved.
EXPLANATION:

•Angular Momentum Conservation: The angular momentum of the system is conserved because there are no external torques acting on the system.

•External Forces: Gravity and forces from the axle act on the turntable, but they do not cause torque around the axle.

•Internal Forces: Forces between the putty and the turntable are internal and cannot change the total angular momentum.

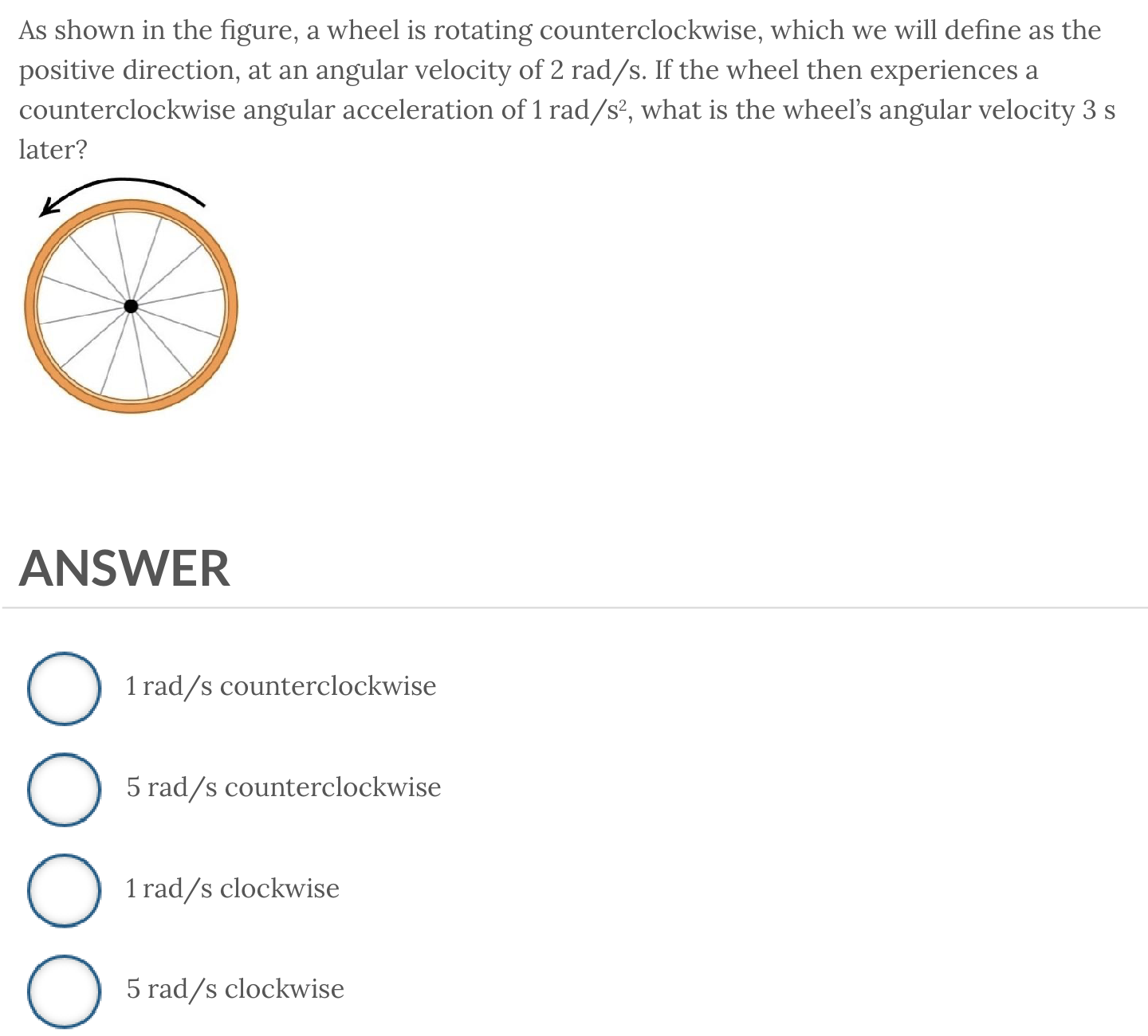
ANSWER: 5 rad/s counterclockwise

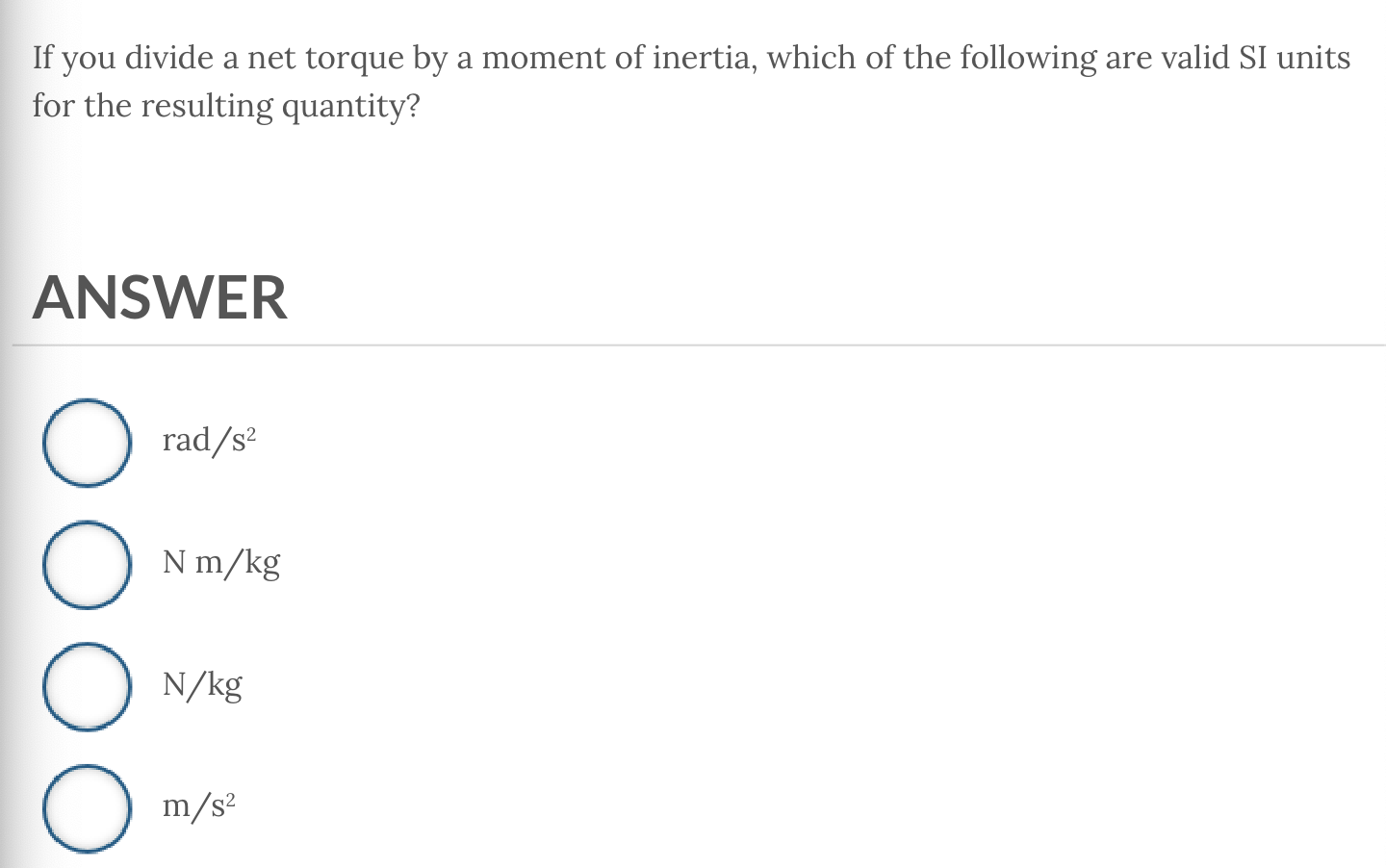
ANSWER: rad/s²

ANSWER: The solid disk

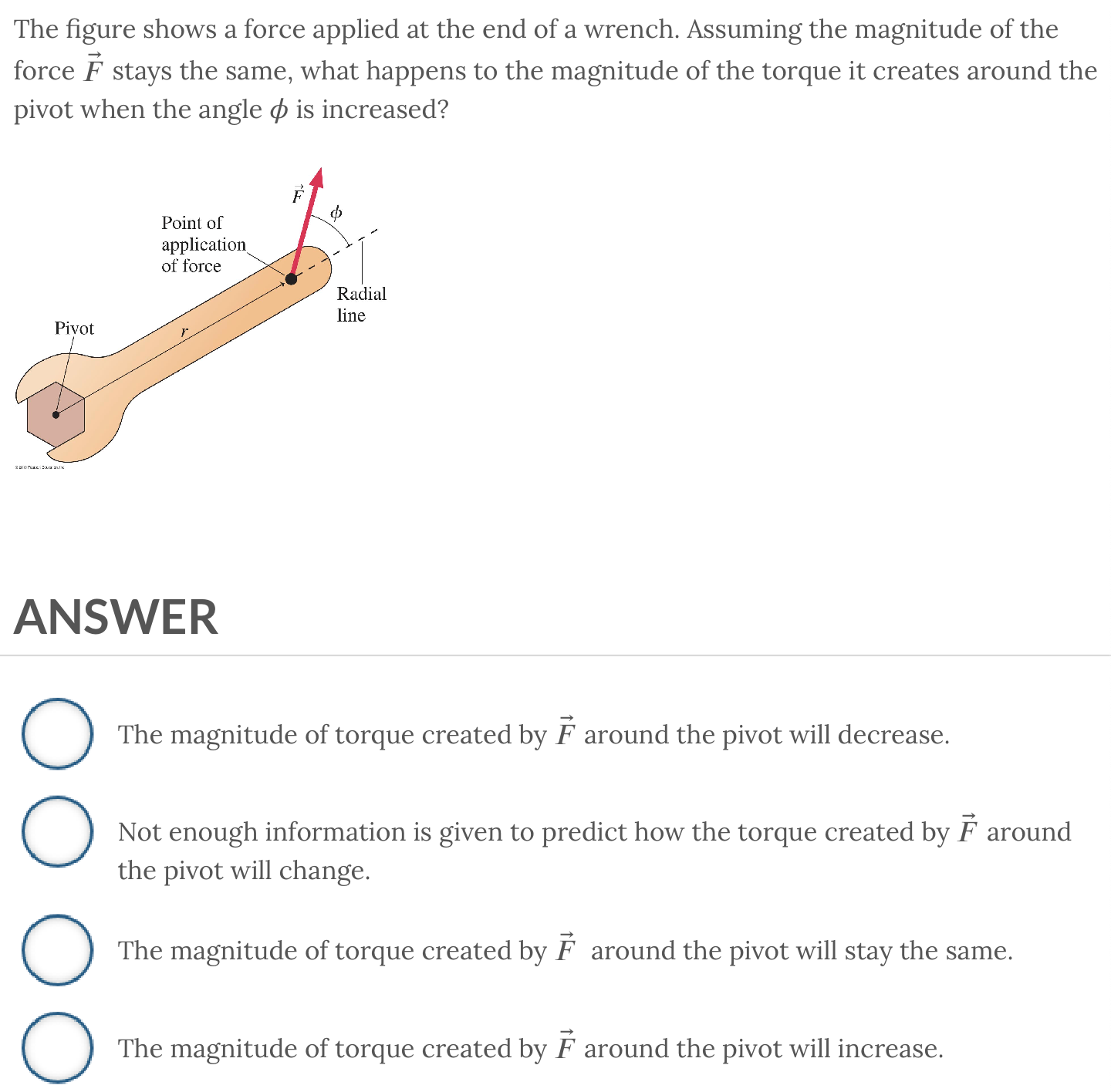
ANSWER: The magnitude of torque created by 𝐹⃗ around the pivot will increase.