Greedy Algorithms

Greedy Algorithms

• Solve your problem in stages

• In each stage, choose the locally optimal choice

• Fast! But for many problems, can be incorrect, or give non-optimal solutions…

• Maybe surprisingly, it turns out that they:

  • Can approximate (for some problems) the optimal solution (and fast),

  • Solve some very well-known problem

Greedy Algorithm for the Euclidian Travelling Salesman Problem

Starting at node 1:

• Repeatedly visit nearest node (to current)

• When you have visited all nodes, go back to origin city

Does not output the shortest route

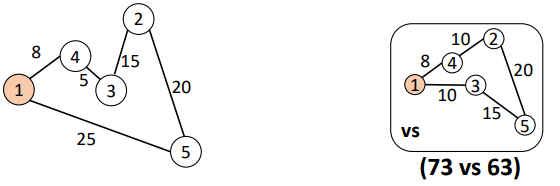
Greedy Algorithm for Shortest Paths

• Start at the source node, and visit in each stage, the (yet) unvisited node which is closest to the source

• This is Dijkstra’s algorithm

• But importantly, it gives an optimal solution to the shortest path computation problem

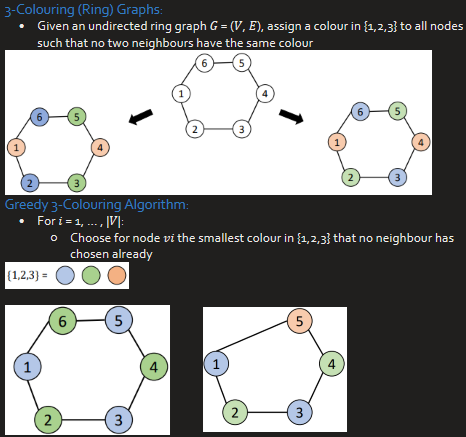
Greedy Algorithm for Vertex-3 Colouring

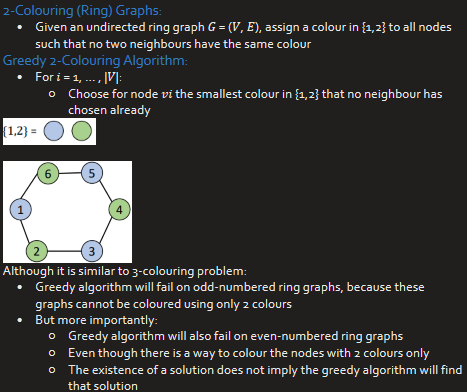
Greedy Algorithm for Vertex-2 Colouring

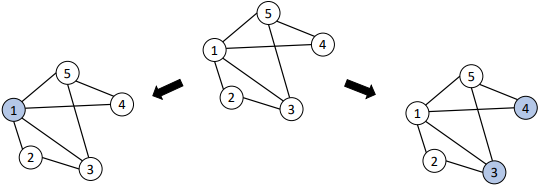
Greedy Algorithm for Maximal Independent Set

Initialize 𝐼 = ∅

For 𝑖 = 1, … , 𝑉 :

• Check if node 𝑣𝑖 has any neighbours in 𝐼

• If not, then add 𝑣𝑖 to 𝐼, or also: 𝐼 = 𝐼 ∪ {𝑣𝑖}

Outputs a correct solution (i.e., an MIS)

Greedy Algorithm for Maximum Independent Set

Initialize 𝐼 = ∅

For 𝑖 = 1, … , |𝑉|:

• Check if node 𝑣𝑖 has any neighbours in 𝐼

• If not, then add 𝑣𝑖 to 𝐼, or also: 𝐼 = 𝐼 ∪ {𝑣𝑖}

Will not output a correct solution (MaxIS) but can output an approximation if all nodes have few neighbours

Greedy Algorithm for Minimum-Weight Spanning Trees (MST)

• Kruskal’s Algorithm

• Prim’s Algorithm

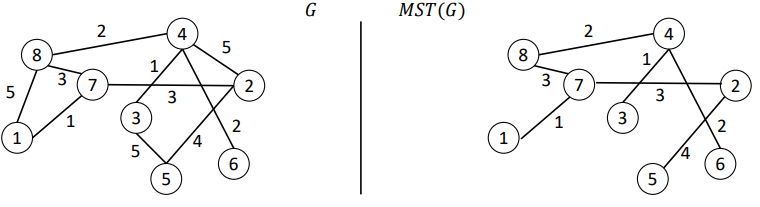
Kruskal’s Algorithm

• Start with tree 𝑇 = ∅,

• Sort edges from lowest to highest weight,

• For 𝑖 = 1, … , 𝐸 :

  • If edge 𝑒𝑖 does not form a cycle when added to 𝑇, then add 𝑒𝑖 to 𝑇, or also: 𝑇 = 𝑇 ∪ {𝑒𝑖}

• Takes 𝑂(|𝐸|log|𝑉|) worst-case time

  • 𝑂(|𝐸|log|𝑉|) time for sorting edges

  • Checking for all |𝐸| edges whether they create a cycle is a bit harder to bound

• Output is a spanning tree is trivial to show (spanning + no cycles)

• Minimum-weight can be shown by proof of induction

  • Induction step is a bit tricky

Prim’s Algorithm

• Start with 𝑉_𝑇 = 𝑣₁ and 𝐸_𝑇 = ∅

• While 𝑉_𝑇 ≠ 𝑉:

  • Find the minimum weight edge {𝑢, 𝑤} going from a node in 𝑇 to a node outside 𝑇,

  • Add {𝑢, 𝑤} to 𝐸_𝑇,

  • Without loss of generality, 𝑢 ∈ 𝑇. Then add 𝑤 to 𝑉_𝑇

• Best implementation gives 𝑂(|𝐸|+|𝑉| log|𝑉|) worst-case time

• Easier implementations give 𝑂( 𝑉²) or 𝑂(|𝐸|log|𝑉|) worst-case time

• Output is a spanning tree is trivial to show (spanning + no cycles)

• Minimum-weight also a bit tricky to show (just as for Kruskal’s algorithm)