1. Algebra 1

axiom

a statement thats can be assumed to be true

steps to a direct proof

assume that a statment P is true

use P to show that another statement Q muct be true

Use direct proof to prove that the square of any intider is one greater than the prodcust of the two integers beside it

Let the integer be n, where n ∈ Z

two numers either side are n-1 and n+1

(n-1)(n+1) = n² - 1

n² =(n+1)(n-1) + 1

therfore the square of any integer is one more that the product of the two integers either side of it

proof by exaustion

show that a statement is true in all possible cases (note only realy workes is there is a specified domain)

disprove by counter example

find any one example that does not fit the statement

quadratic formula in words

x equals minus b puls or minus the square root of b squared minus four a c all over 2 a

discriminant

b²-4ac

how to prove the quadratic formula

complete the square and then slove

coordiates of the vertex for a(x+p)² + q

(-p,q)

discriminent = 0

tangent

the equation of a circle centre (-3,4) and radius 9

(x + 3)² + (y - 4)² = 81

angles in a cyclical quadrilatral

opposire agles in a cyclic quadrilatral add to 180

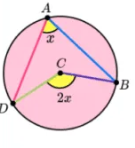
angle at the centre theorem

the angle at the crentre is twice the angle at the circumfrence

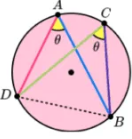
Angles in the same segment theorem

Angles in the same segment are equal

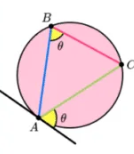
alternate segment theorem

the angle that lies between a tangent and cord is equal to the angle subtended by the same cord in the alternate segment

what is the angle in a semi circle

90

cord of a circle theorem

the perpendicual from the centre of a circle to a cord besects the cord

how are inequalitites represented on a number line

≤ ≥ filled in circle

< > outline of a circle

how do you use brackets to represent inequalities

≤ ≥ square brakets [ , ]

< > round brackets ( , )

how do draw inequalities on a graph

≤ ≥ normal line _____

< > dotted line _ _ _ _