Scientific Notation, Measurement, and Problem Solving in Chemistry

Unit

A unit is a standard, agreed on quantity by which other quantities are measured.

Scientific Notation

A method to write large and small numbers more compactly.

Positive Exponent

A positive exponent (n) means 1 multiplied by 10 n times.

Negative Exponent

A negative exponent (−n) means 1 divided by 10 n times.

Scientific Notation Format

A number written in scientific notation consists of a decimal part, exponential, and exponent parts.

Population of China (2017)

1,387,000,000 people = 1.387 x 10^9 people.

Scientific Notation Example

0.00000867 = 8.67 x 10^-6.

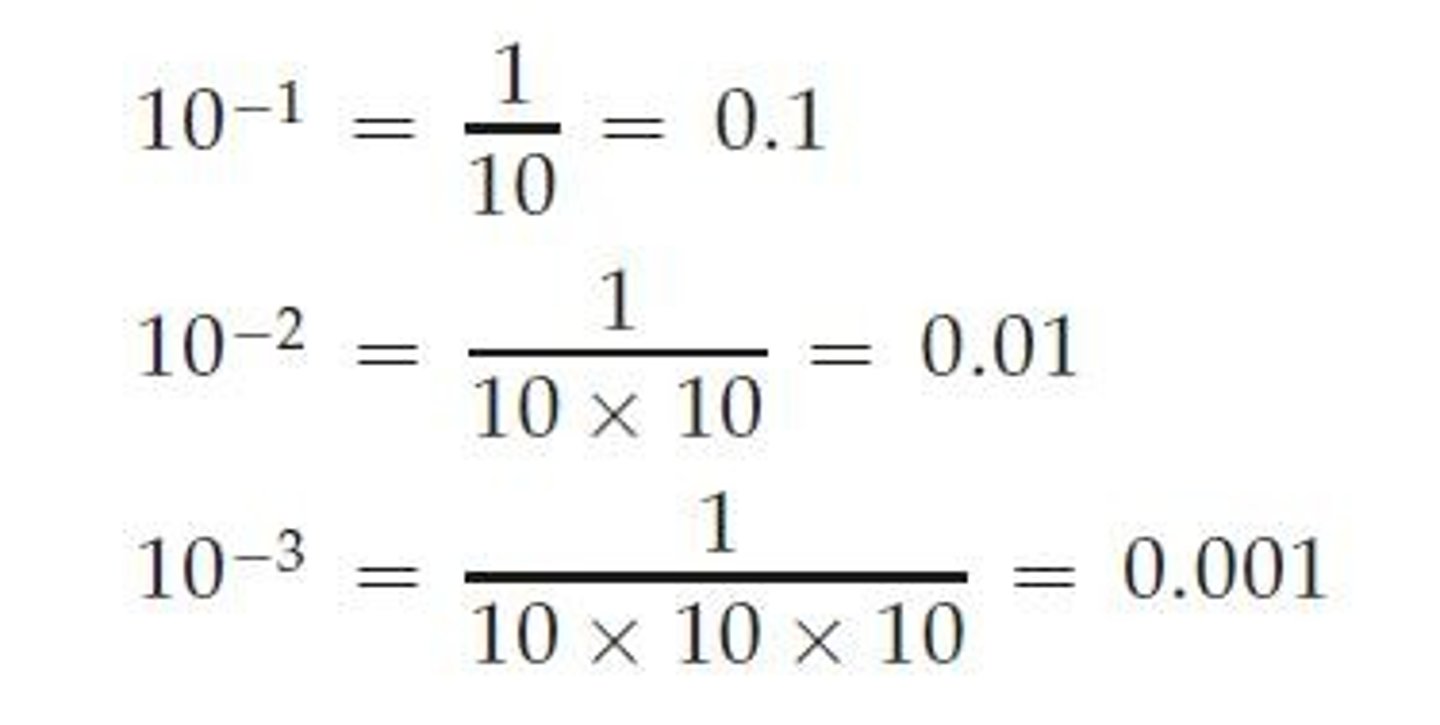
Precision in Measurement

Scientists adhere to a standard way of reporting measured quantities in which the number of reported digits reflects the precision in the measurement.

Temperature Increase Reporting

The average global temperature has risen by 0.7 °C since 1880, meaning 0.7 ± 0.1 °C.

Significant Figures

The non-place-holding digits in a measurement are significant figures (or significant digits).

Precision of Measurement

The greater the number of significant figures, the greater the precision of the measurement.

Leading Zeros

In the number 0.002, the leading zeros mark the decimal place; they do not add to the precision of the measurement.

Trailing Zeros

In the number 0.00200, the trailing zeros do add to the precision of the measurement.

Significant Figures in 350

350 = 3.5 x 10^2 (two significant figures); 350 = 3.50 x 10^2 (three significant figures).

Decimal Point Movement

If the decimal point is moved to the left, the exponent is positive; if moved to the right, the exponent is negative.

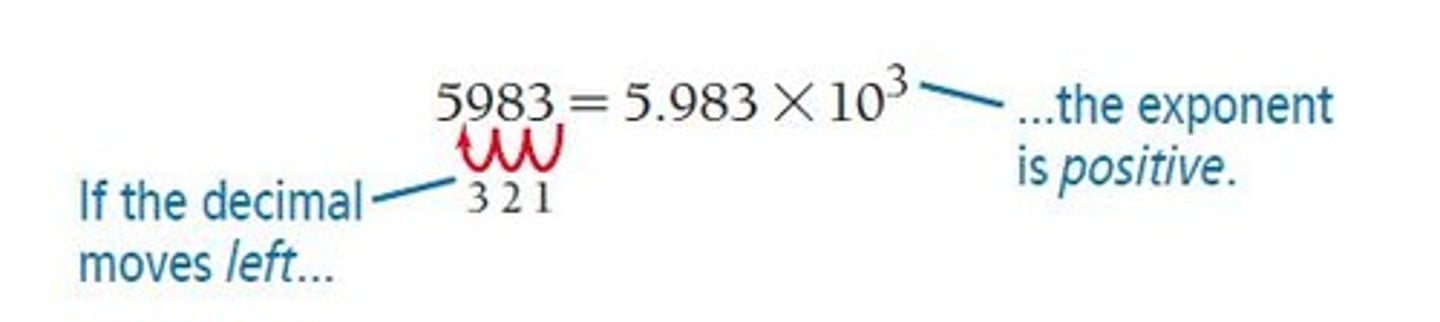
Measurement Example (Copper Sulfate)

The correct reading is 1.3 g, estimated from a balance with markings every 1 g.

Measurement Example (Pistachio Nut)

The correct reading is 1.26 g, estimated from a balance with markings every 0.1 g.

Reported Digits

More digits indicate more precision; fewer digits indicate less precision.

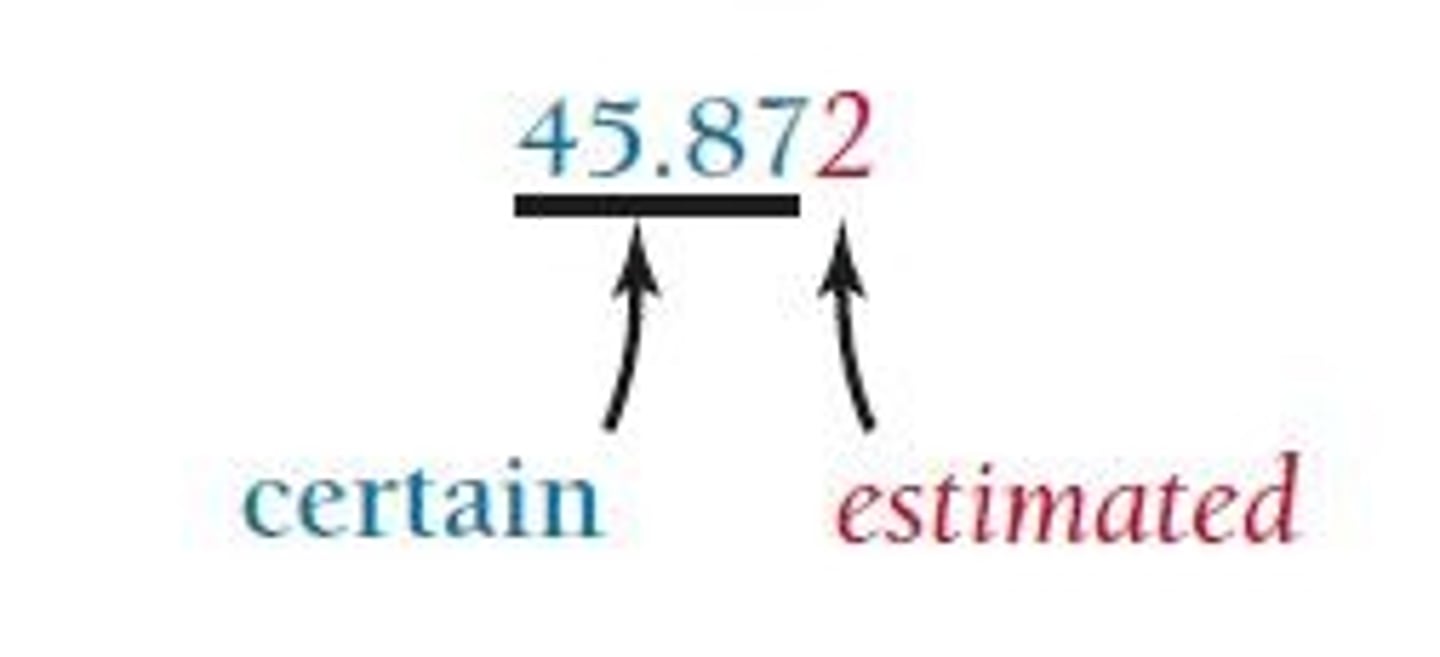
Last Reported Digit

The uncertainty in a measurement is indicated by the last reported digit.

Measurement Overstatement

It would be incorrect to report 24.60 mm because it overstates the precision of the measuring device.

Conceptual Question

A question that prompts deeper understanding of the topic.

Example of Reporting Temperature

Answer: 103.4 °C.

Exact Numbers

Numbers that have an unlimited number of significant figures.

Defined Quantities

Quantities that are exact, such as the number of centimeters in a meter.

Ambiguous Significant Figures

A situation where the number of significant figures is unclear, such as in the number 2100 without a decimal point.

Rounding Rules

Round down if the last digit dropped is 4 or less; round up if it is 5 or more.

Addition and Subtraction Rule

The quantity with the fewest decimal places determines the number of decimal places in the answer.

Multiplication and Division Rule

The quantity with the fewest significant figures determines the number of significant figures in the answer.

SI Units

The International System of Units, the most convenient system for scientific measurements.

Mass

A measure of the quantity of matter within an object.

Weight

The gravitational pull on an object, calculated as W = mg.

Kilogram

The base unit of mass in the SI system, equivalent to 1000 grams.

Gram

A common unit of mass defined as 1/1000 of a kilogram.

Significant Figures in 2100

2100 can have different numbers of significant figures depending on whether it's written with a decimal point or in scientific notation.

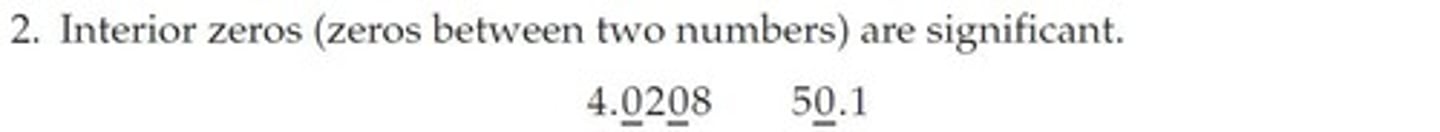
Example of Rounding

To round 2.349 to two significant figures, it becomes 2.3.

Example of Multiplication

3.489 x (5.67 - 2.3) = 12 (2 significant figures).

Example of Addition

3 + (1.25) = 4.25 = 4 (one significant figure).

Example of Division

18/12 = 1.5 (two significant figures).

Integral Numbers

Numbers that are part of an equation and considered exact.

Prefix Multipliers

Used in the SI system to denote multiples or fractions of units.

Acceleration due to Gravity (g)

The gravitational pull on an object, which varies depending on the planet.

SI Prefix Multipliers

They change the value of the unit by powers of 10.

1 km

1000 m = 10^3 m

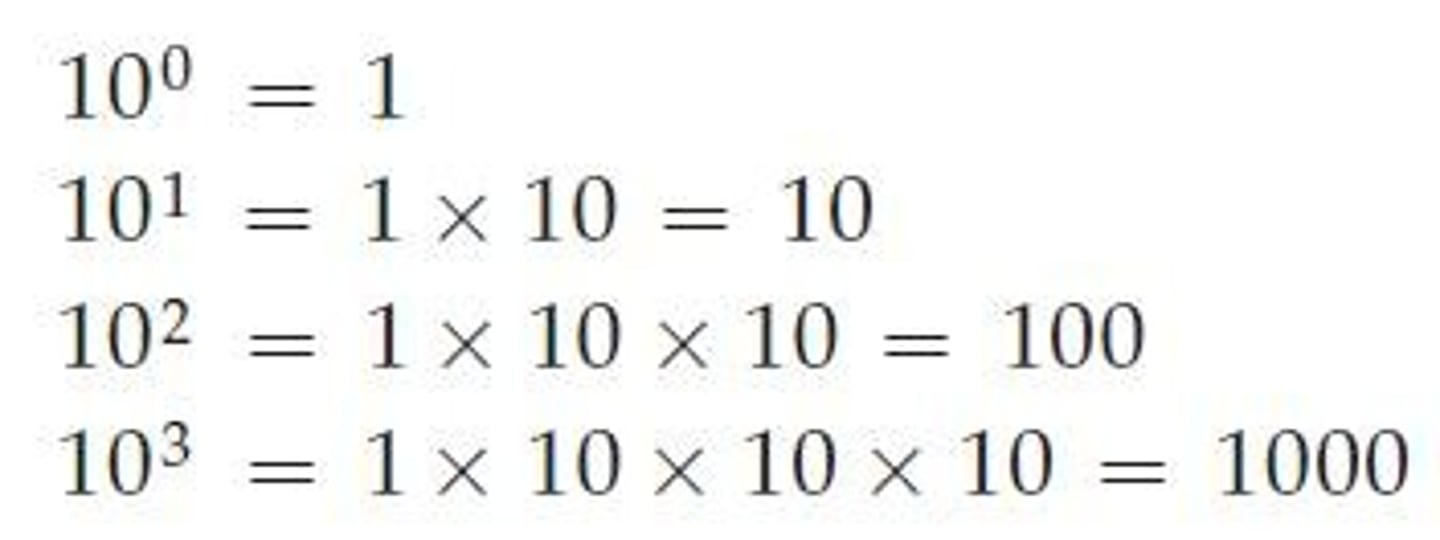
1 ms

0.001 s = 10^-3 s

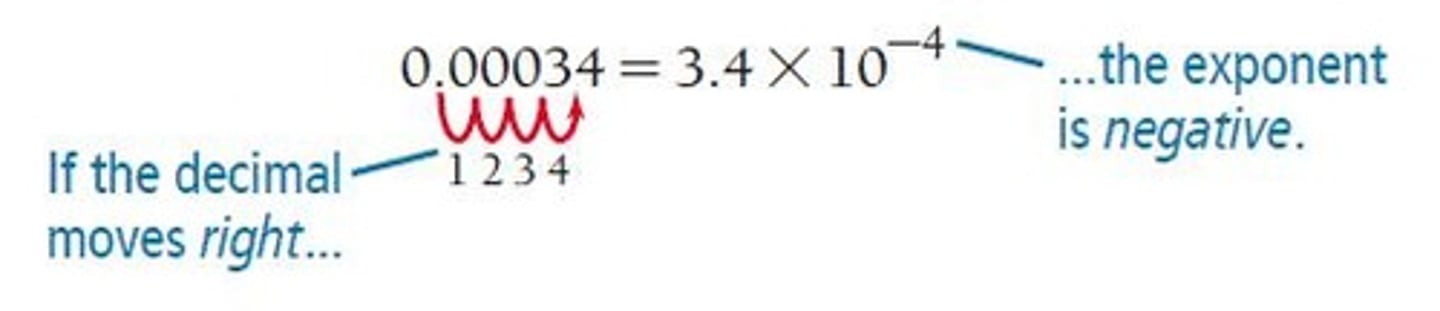
Derived units

A derived unit is formed from other units.

Volume

Any unit of length raised to the third power.

Density

Mass per unit volume.

Speed

Distance covered per unit time.

Dimensional analysis

Using units as a guide to solving problems.

Conversion factor

A quotient with the desired unit on top and the given unit on the bottom.

1 in.

2.54 cm

1 ft

12 in.

Velocity of a car

65 km/hr = 18 m/s.

Cubic centimeters (cm3)

Units raised to a power must have the conversion factor raised to that power.

Density of a substance

The ratio of its mass to its volume.

Density units

g/cm3 or g/mL.

Density of water

1 g/mL.

Density of mercury

13.6 g/mL.

Density of the Dead Sea

1.24 g/mL.

Density of sea water

1.03 g/mL.

Density calculation example

Density = 9.67 g / 0.452 cm3 = 21.393 g/cm3.

Volume measurement example

To measure 68.4 g of a liquid with a density of 1.32 g/cm3.

Mass (m)

35 mg.

Density (d)

0.788 g/cm3.

Volume from mass example

35 mg x (1 g / 1000 mg) x (1 cm3 / 0.788 g) = 0.044 cm3.

Solution for 1000 cm3

0.82 L x (1 L) x (19.3 g / 1 cm3) x (1 kg / 1000 g) = 15.826 kg.

Definition of Chemistry

Chemistry is the science that seeks to understand how matter behaves by studying what atoms and molecules do.

Atoms

Atoms are the building blocks of matter and are incredibly small.

Molecules

Atoms come together to form different types of molecules, and the characteristics of a molecule depend on the atoms it contains and how it is shaped.

Water Molecule

Water is comprised of one oxygen atom and two hydrogen atoms and has a bent shape.

Temperature Range of Water

Water remains a liquid over a large temperature range, making it an ideal molecule to sustain life.

Chemicals

Chemicals make up virtually everything around us, including things we can hold or touch.

Common Chemicals

Examples of common chemicals include skin (keratin), soda (water, sugar, carbon dioxide, caffeine), and pencil lead (graphite).

Narrow View of Chemicals

People often think of chemicals only as dangerous poisons or pollutants.

Scientific Method

The scientific method is a way of learning that emphasizes observation and experimentation to understand the world.

Geocentric Theory

The geocentric theory posits that Earth was the center of the universe, based on philosophical reasoning.

Heliocentric Theory

The heliocentric theory posits that the Sun was the center of the universe, based on astronomical observations by Nicolaus Copernicus.

Anthropocentric View

The anthropocentric view reflects that humans and their environment were central to the cosmos.

Chemists' Questions

Chemists are interested in why ordinary substances are the way they are, such as why is water a liquid or why does soda fizz.

Examples of Ordinary Substances

Ordinary substances include the air we breathe, the water we drink, toothpaste, Tylenol, and toilet paper.

Importance of Chemistry

Chemistry helps us understand the composition and behavior of ordinary things.

Atoms in Sand

A single grain of sand contains more atoms than there are grains of sand on a large beach.

Nature of Water

The nature of the water molecule determines how water behaves.

Liquid Water

If the water molecule were linear, it would be a gas.

Chemicals in Everyday Life

Chemicals compose ordinary things, such as paint thinner and rivers polluted by industrial waste.

Chemistry and Life

Chemistry is essential for understanding the substances that sustain life.

Chemistry's Role

Chemistry plays a crucial role in understanding the materials and processes that affect our daily lives.

Chemists' Methods

Chemists use the scientific method to answer questions about the nature of substances.

Chemistry's Impact

Chemistry impacts various aspects of life, from health to environmental issues.

Observation

The first step in acquiring scientific knowledge, involving the measurement or description of some aspect of the physical world.

Simple Observations

Observations that require only the naked eye, such as 'Snow is white' or 'A body is either at rest or in motion.'

Sensitive Instruments

Tools needed for some observations, such as microscopes to see red blood cells shaped like a biconcave disk.

Hypothesis

A tentative interpretation or explanation of observations, often formulated after making observations.

Falsifiable Hypothesis

A good hypothesis that can be proven wrong through further testing.

Experiments

Highly controlled observations designed to validate or invalidate a hypothesis.

Experimental Results

Outcomes of experiments that may confirm a hypothesis or require modification or replacement of the hypothesis.

Law

A brief statement summarizing past observations and predicting future ones, developed from a number of similar observations.

Newton's First Law of Motion

A law stating that a body is either in a state of rest or continuous motion unless acted upon by an external force.

Law of Conservation of Mass

A law stating that in a chemical reaction, mass is neither created nor destroyed, developed by Lavoisier based on combustion observations.

Scientific Theory

A basis formed from one or more well-established hypotheses that provide broader and deeper explanations for observations and laws.