HL AI - Matrices

Matrix Order Notation

m x n (m rows, n columns)

Element of a Matrix Notation

a_ij (i indicating the row, j indicating the column)

Adding and Subtracting Matrices

add or subtract elements in the same position

Scalar Multiplication of Matrices

multiply each element by the scalar

What allows matrices to be multiplied?

the number of columns in the first matrix must be equal to the number of rows in the second matrix (eg. 2×3 and 3×3)

Multiplying Matrices

multiply the rows in matrix one by the columns in matrix two

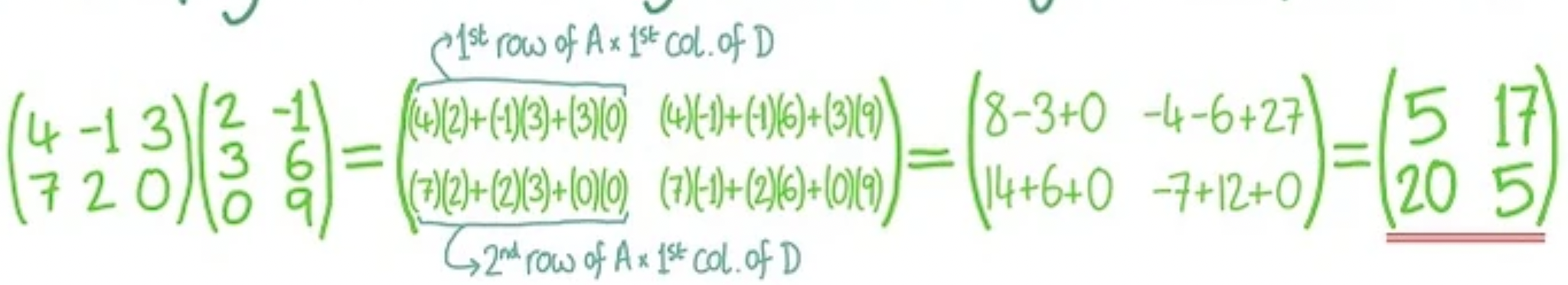
Properties of Matrices

Inverse of a Matrix

a matrix that can be multiplied with the original matrix to form an identity matrix

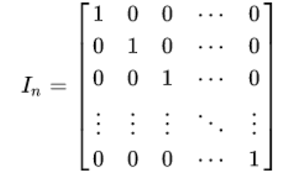
Identity Matrix

a matrix which contains ones on its main diagonal while the rest of the matrix elements are zeros

Finding an Inverse Matrix

can be done on a GDC (put the matrix to the power of -1), or use the method pictured

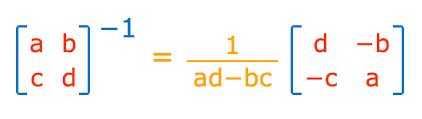
Determinant of a Matrix

ad - bc

Solving Systems of Equations

1. rewrite the system of equations as a matrix equation (like pictured)

2. multiply both sides by the inverse of the matrix on the side with the variables (in order to get the variable on their own)

3. determine the answer

Using Transformation Matrices

1. create a position vector (x over y)

2. use the formula booklet to create a transformation matrix

3. multiply the 2×2 matrix with the 2×1 matrix to get a final position vector

Composite Transformations

transformations that happen one after the other (the transformation that comes first is written second, so AB means B happens first)

Finding the Area of a Transformed Image

if an object is transformed by matrix A, then: new area = DetA x original area