Extension 1 maths

Polynomials

SKIP

What is a polynomial

A polynomial is a mathematical expression in which contains variables and numbers, where variables are raised to a whole number power and the terms are added, subtracted or multiplied

Not polynomials examples

Examples of non polynomials are

• negative powers: 1/x

• fractional powers

• logs

• powers of x

What is a leading term

A leading term is the highest number and power

Degrees of the sum and difference

If P(x) and Q(x) are polynomials with degrees n and m:

Case 1:n ≠ m: when you add or subtract, the degree stays the same

Case 2: n = m: the degree drops or disappears if they cancel

Identically equal polynomials

Polynomials are identically equal when P(x) and Q(x) are the same for all values of x

P(x) ≡ Q(x)

Tip when the polynomials are Identically equal

• for questions asking for a, b c you can add polynomials by equating coeffcients

When you derive a polynomial is it even or odd? Why?

It becomes odd as P(x) is even in which an even polynomial has only even powers so when it is derived it becomes odd as every term in p′(x) has odd power ⇒ p′(x) is odd.

( works other way around if P(x) is odd)

Division of polynomial formula

P(x)= D(x) ⋅ Q(x) + R(x)

Rational Form

P(x)/D(x)= Q(x)+ R(x)/D(x)

Tips when finding a and b to make it exactly divisible by x

Make set a and b as the remainder and equate coefficient so:

Set remainder = 0.

Equate coefficients of like powers.

Solve for a, b.

Remainder Theory

If you divide a polynomial by (x − Φ), the remainder is the value of the polynomial at x = Φ.

Suppose P(x) is a Polynomial and Φ is a constant

then R(x)= x-Φ = P(Φ)

Why does this work

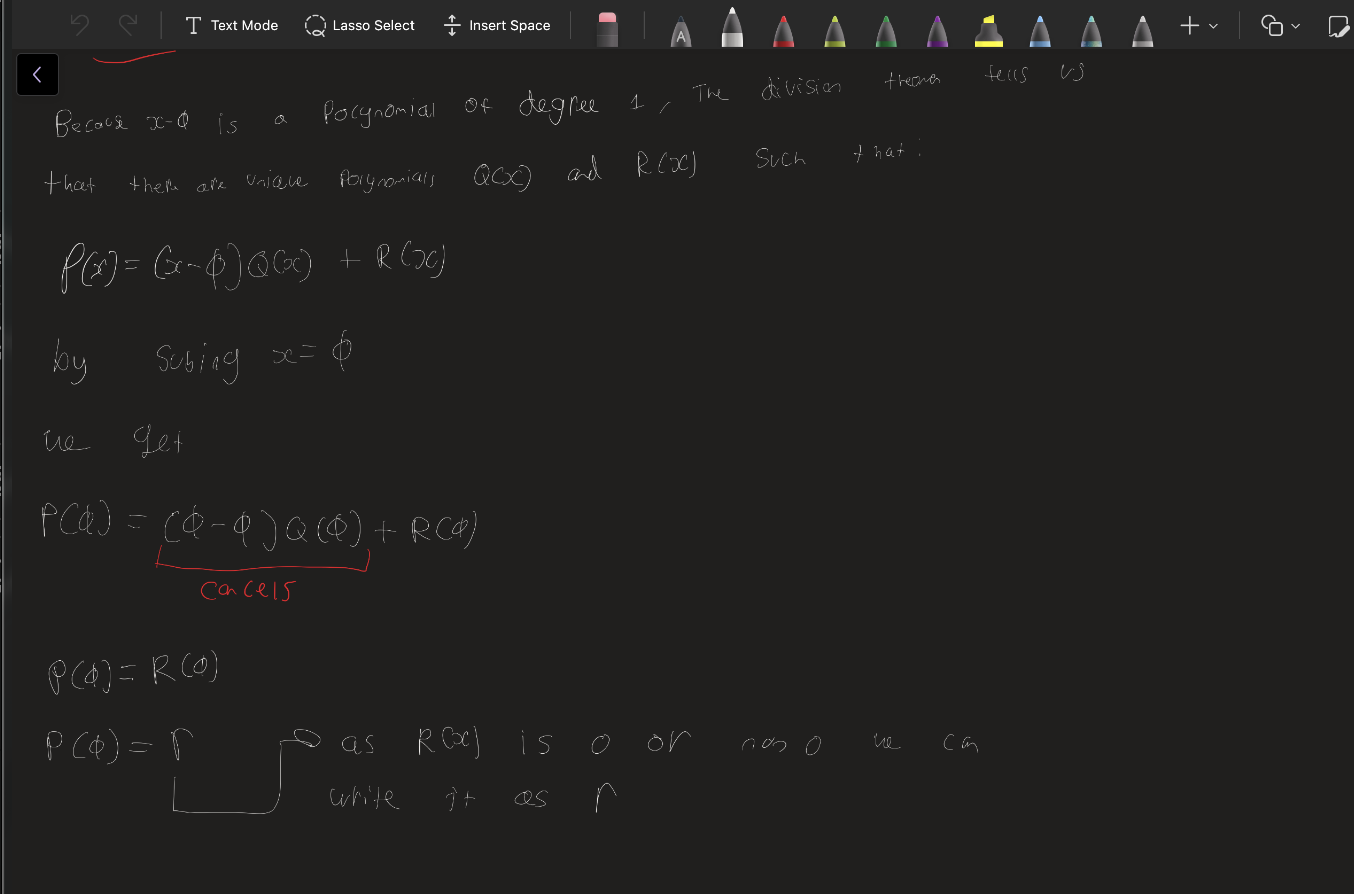
What is the Factor Theorem

If a polynomial f(x) is divided by (x − a):

• If the remainder is 0, then (x − a) is a factor of the polynomial.

• If the remainder is not 0, then (x − a) is not a factor.

Proof for this theorem

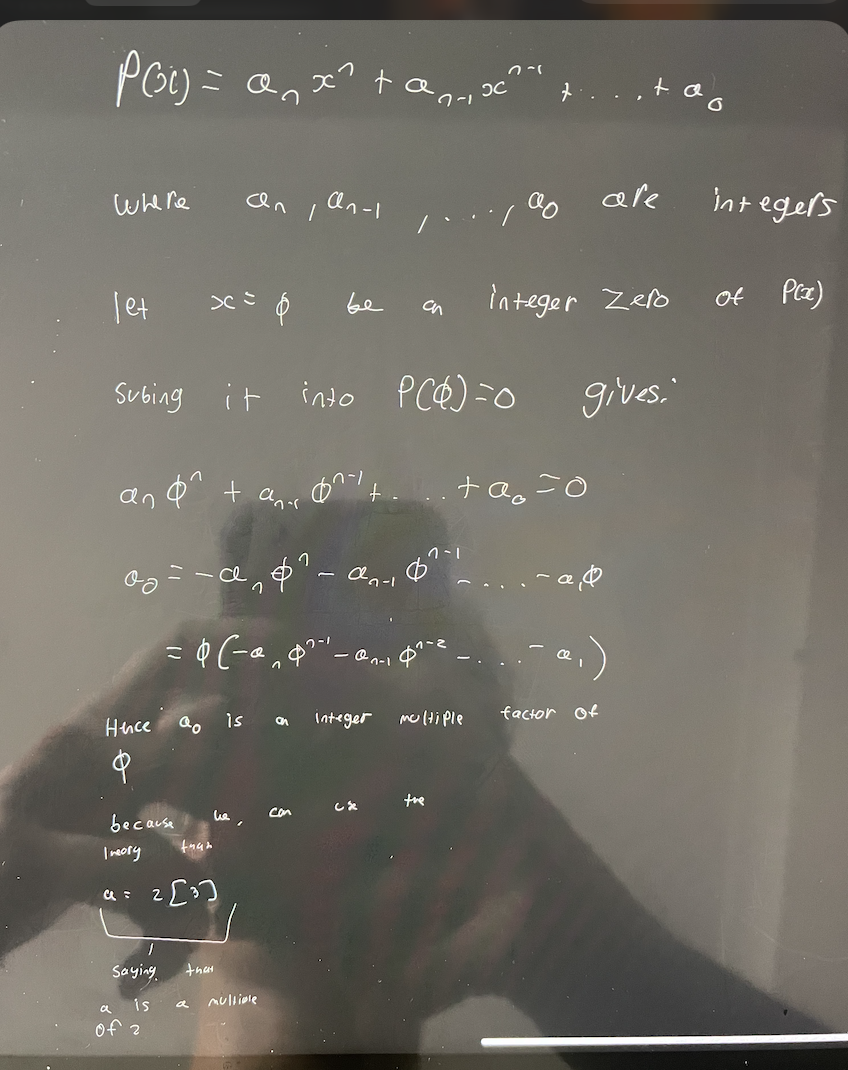
What are Distinct Zeroes

Distinct zeroes of a polynomial are the different values of x that make the polynomial equal to zero, counted only once each.

Suppose that Φ_1,Φ_2……Φ_n are zeroes of the polynomial P(X)

Then: (x-Φ₁),(x-Φ₂)…..(x-Φ_n) are factors of P(X)

The proof for this

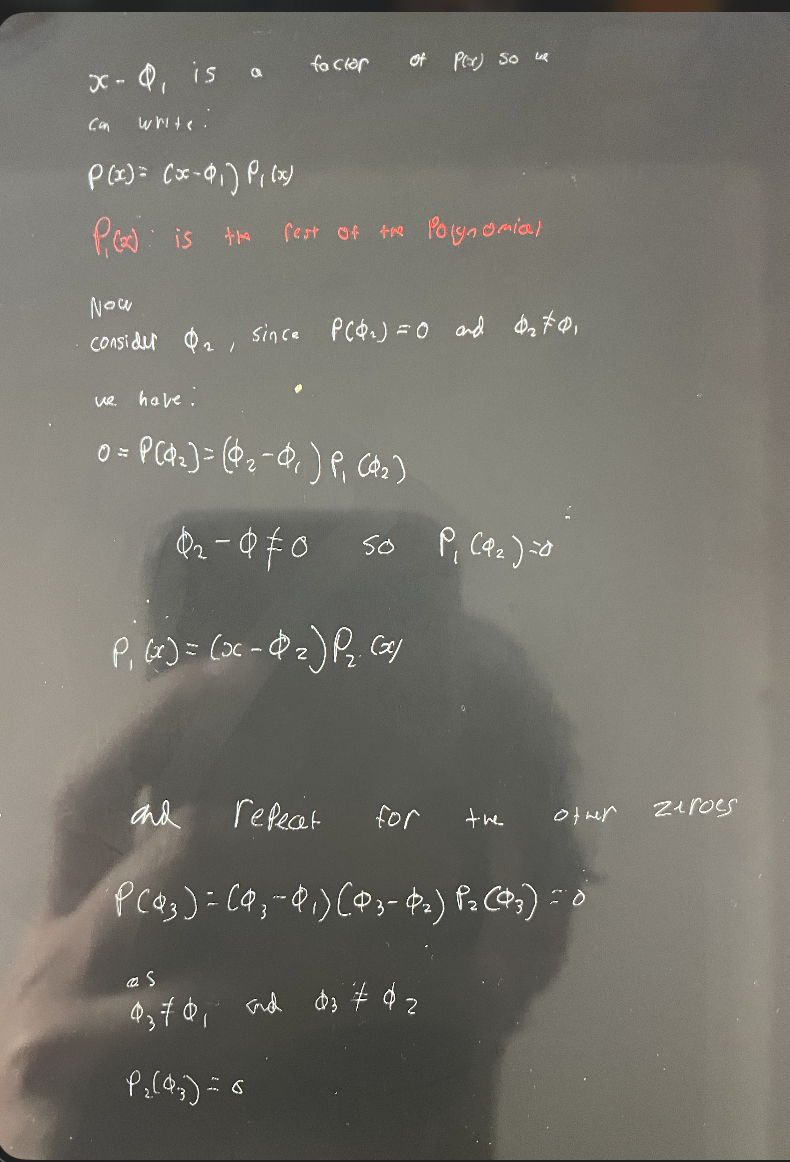
The vanishing Condition

Supposed P(x) has degree at most n and it is a zero at n+1 then P(X)≡ 0

Tip for this

• If it says it has 3 zeroes sub in 0 to find a,b and c

• if two polynomials have degrees m and n, where m>n then the maximum number of intersections is m

• The reason why a cubic with 3 distinct zeroes must have 2 stationary points are because when we derive the polynomial it’ll give a quadratic hence having only 2 real roots.

Multiple roots

if Φ is a multiple root of P(x), then the graph y=P(x) has a stationary point at x=Φ

Another rule for multiple root is

When we have the polynomial in the form of (x-Φ)^mQ(x), where Q(x) is not divisible by x-Φ from the factor theorem that Q(x) is only divisible by x-Φ when Q(Φ)=0

Behaviour at simple and mulitiple zeroes 1.

if x=Φ has even multiplicity then the curve is tangent to the x axis at x=Φ and does not cross the x axis so the point (Φ,0) is a turning point

if x=Φ has odd multiplicity at least 3 then the curve is tangent to the x axis at x=Φ but crosses the x axis at (Φ,0) making it a horizontal inflection

3.

if x=Φ is a simple zero then the curve croesses the x axis at x=Φ in which theres no stationary points there.

formula for absolute value of alpha + beta

sqr (alpha + beta)²

Further functions (nothing)

how to graph reciprocals

we find values of x when y = + - 1

then we find asyomtotes

then we graph

How to find maximum value of reciprocal

1. f’(x)

2. equal to zero

3. solve for x

4. imput to f(x)

how to do sums and products of function.

just add or times the values together but always keep checking where itll be headed as if f(x) is below G(x) when x=n then itll make it negative

How to sketch absolute value of y = f(x)

• delete everything in the below x axis then replace it by duplicating it on the other side

• everything above the x axis stays the same

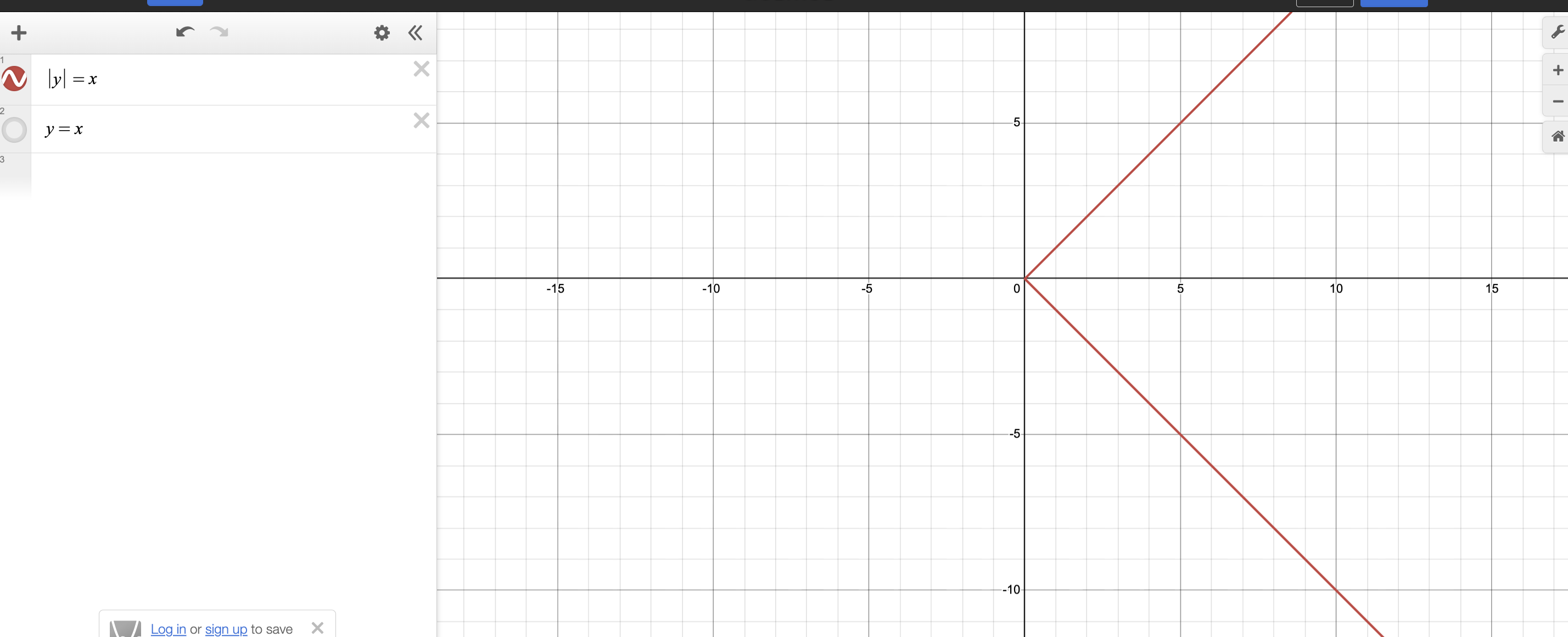
how to graph y= f( absolute value of x)

• delete everything from the left and keep everyting to the right. then duplicate it to the left

y= absolute value of f(x)

just move everything thats below the x axis up above it

Tips to draw square root graph

f(x) < 1 it’ll be higher

f(X) > 1 it’ll be lower

How does inverse functions work and what happens to the domain and range

we reverse x and y so the domain becomes the range and the range becomes the domain

how to do trig parametrics

1. isolate cos and sin

2. sub sin² +cos² =1

3. solve

Further trig (nothing)

formula for cos(A+ - B)

CosACosB - + SinASinB

Formula for SIn(A + - B)

SinaCosB + - CosASinB

Formula for Tan (A + - B)

TanA + - TanB / 1 - + (tanA)(TanB)

formula for sin2A

2sinACosA

formula for cos2A

cos²A - Sin²A

Formula for Tan2A

2TanA/ 1 - tan²A

What does “t” equal to in the t formula

t = tan x/2

sinx using t formula

2t / 1 + t²

cosx using t formula

1 - t² / 1+ t²

tanx using t formula

2t / 1 -t²

SinAsinB formula

½ [cos(A-b) - Cos (A+b)

CosACosB

½ [ Cos(A-B) + Cos(A+b)]

SinACosB

½ [sin(A+B) + Sin(A-B) ]

CosASinB

½ [ Sin(A+B) - sin(A-B)

Combinatorics

The two formula for N!

N! = n times (n-1) times (n-2) …..

N! = n times (n-1)!

Formula for (n-r)!

(n-r) ( n-r-1)

Formula for (K+1)! - K!

K! [ (K+1) -1 ] = K times K!

Tips on when to use

• arranging lines

• queue

• placed in first second third…..

formula for when “two people in a line must be together

(n-1)(x)

n = total number of people

• x = number of ways the people inside the block can be arranged

note

2 people : 2! ( n-1)

3 people: 3! (n-2)

how to choose number of ways of choosing a completed section

multiply everything

eg

12 shirts

6 pants

= 12 times 6

how to do ordered selection with repetition

the number of r letter words formed from n distinct letters with repetition is equal to n^r

(dont use factorials)

eg

How many 4-letter words can be formed using the letters A, B and C

n = 3

r = 4

What is permuatation

is an arrangement of objects chosen from a set without repetition and replacement in which where order matters.

Formula for permuatation

n p r = n! / (n-r)!

n = total avalible

r = items chosen and arranged (how many were used)

eg

the permuation of 3 distinct letters take from 5 letter set

n = 5

r = 3

What does n p n equal to

n!

Question types of permuations

• pins: if it doesnt say the amount then assume it’ll be 10

• words with no repeating letters

block method for permuatation

(n-r+1) times r!

• n total objects

• r objects that must be together

when to us eblock method and when to not

• Must be together” → block method

• “Must NOT be together” → total arrangements − together arrangements

tips for ordered selections and grouping

• order the groups then order the people in the group

• cases should never overlap

• always times each case by the amount of ways they can be arranged

if letters are together what to do

group them as one

ordered selection with identical elements

n! / r1! times r2! ….

use when there are multiple of the same letter/ variable

how to do seperated letters with identically element s

Total arrangements - S’s togethr

for S c S

arrangement together for identically elements: (n-r+1)!/ factorial of repeats

how to do questions like “how many n letter words can be formed using _____”

"1. make cases if theres 2’ns or 3 n’s

2. times

combination formula and meaning

it is the set order of objects where order doesnt matter

formula is n C r= n!/ (n-r)! times r!

variation of this

(n r)

n c r = n c n-r

next 10 slides are for circles. note: n= total and k = number of objects that must be together

No restrictions

(n-1)!

two people must sit apart

(n-1)! - [(n-2)! times 2!]

boys and girls alternating

(b-1)! times g!

1. arrange boys in a circle

2. arrange girls in the gaps

3. solve

opposite from each other

(n-2)!

two of the same boys next to each other

2(n-1)!

all boys together

(n-k)! times k!

k = amount of boys

Rules for pigeonhole principle and the meaning

r = 0 : one pigeonhole with Q pigeons

r > 0 : one pigeon hole with Q+1 pigeons

If more objects than containers, at least one container holds multiple objects.

How to solve pigeon hole questions

1. identify n

2. identify k

3. use n/k

n = number of items

k = places they can go

binomial expansion

its just

(x+y)^n = n c o times x^n + n c 1 times x^n-1 times y

Further calc (nothing)

formula

Q = Ae^kt

Dq/Dt = KQ

what are the variables meaning

A= is the inital value

k = growth constant

another way of expressing Dq/Dt and what is A here

k( Q-b)

in which

Q= B +Ae^kt

A = the value of Q-B at t=0

Yr 12 Trig (nothing here)

What does cos² x and sin² x equal to

½ + ½ cos2x

½ - ½ cos2x

Tips when doing trig equations

• get all the angles the same

• get all the trig functions the same

What is a homogeneous equation

IT is called a homogenous equaion in sinx and cosx if the sum of the indices of sinx and cosx in each term are the same. So pretty much

A homogeneous equation is an equation where every term has the same degree.

Simply:
If you multiply all variables by a number, the whole equation scales consistently.

How to solve a homogenous equation

divide through a suitable power of cosx to produce a equation of tanx

Steps in solving

1. use formulas (compound, t etc etc)

2. reduce to variables (if needed)

3. look for similarities to move to the same side

4. determine if its homogenous

5. divide sides by cosx

6. solve

Auxiliary angle method

it says that any f(x) = asinx +bcosx can be rewritten in the forms of

y = Rsin (x- alpha)

y = Rsin( x + alpha)

y = Rcos( x - alpha)

y = Rcos( x + alpha)

What is R

R is equal to the square root of a² + b²

Steps to do this

1. set them to equal y or f(x)

2. equate coeffcients sinx and cosx

3. squaring them (for sin² +cos²=1) then add

4. solve R

5. find alpha

6. put equations together

Yr 12 stats

Bernoulli trials

is a single stage random experiment with two outcomes (success) and (failure) in which we asign them as

p =( changes depending on situtation but it is the success)

q = 1 - p = ½ (failure)

Binomial experiments

n stage experiments in which

• each stage is a bernoulli trial

• stages are independent'

• random variable x is the number of success and order is irrelevant

Formula for this is

P( x success) = ncx times p^x times q^n-x

p (x success) = ncx times (1/2)^n ( for p=q)

probability of one specific order: P = p^x times q^n-x

(p + q) = 1^n = 1

TIp to understand this better. P(two are clubs) and P(at least one is a)

P(two are clubs) = 6 c 2

P(at least one is a ) = 1 - p(all are non )

How to do questions like P(2 girls and 3 boys) for 5 people

1. set x = 2 or 3

2. use formula '

3. done

as if you have success 2 girls then through inspection you have 3 boys