IPR - WEEK 6 - Normal distribution and Z-scores

Distribution of data

• Overall shape and pattern of the data

• how the data looks overall, how the data are arranges or spread across values

What does distribution of data look at?

• Shape - overall pattern

• Symmetry - if the left and right sides mirror eachother around the centre

• tails - thin ends of the distribution curve (extreme values)

• long tails - more outliers

• heavy tails = higher cnances of extreme values

• influence testing = rare eventds fall i the tails

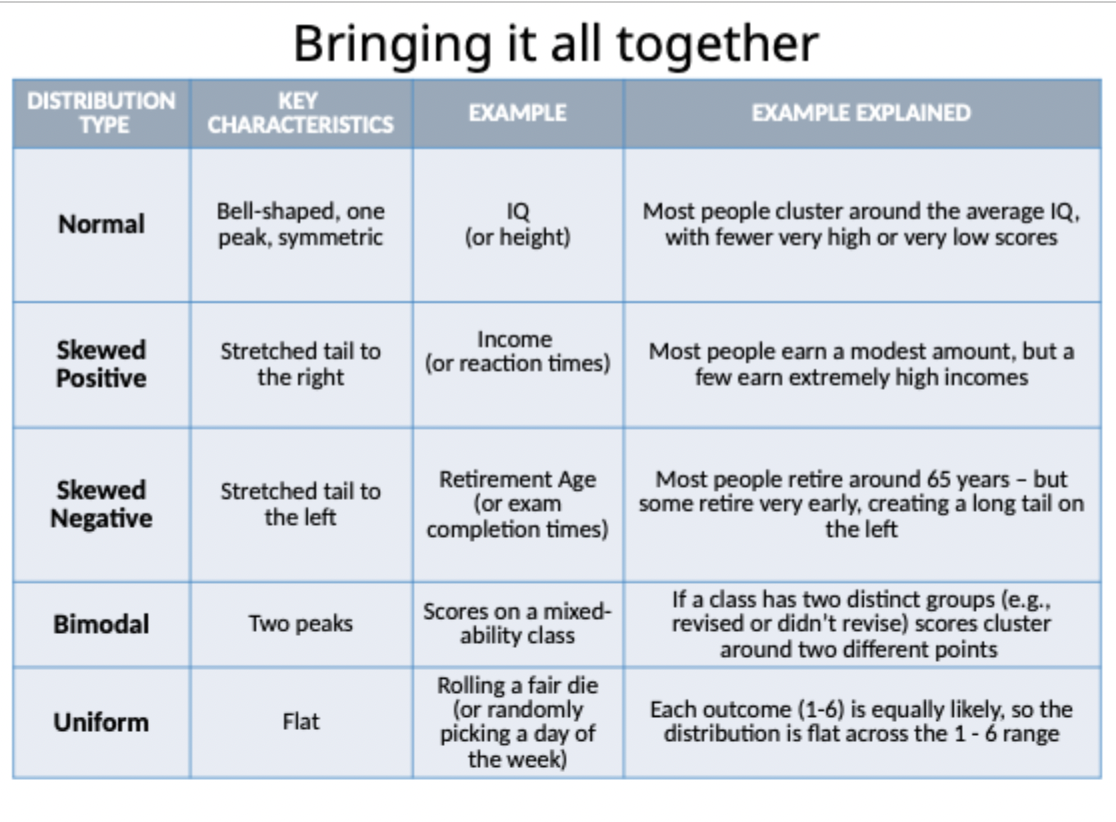
What are common distributions of data?

• Normal (bell-shaped, symmetric)

• Skewed (tail longer on one side)

• Bimodal (two high points

• Uniform ( flat, values spread evenly

What is a normal distribution?

• Bell shaped

• cluster around the centre (one peak

• symmetric on both sides of the peak (the mean)

• tails = fewer values as you move away from the centre (extremes)

• a perfectly normal distribution: = mean = median = mode

What is skewed distribution?

• The asymmetical nature of a distribution

• tail stretched more on one side

• left and right sides are not mirror images

• one peak, most values cluster on one side of the peak

• has two different types of skewed

What are the two different skewed distributions?

• Positively skewed

• Negatively skewed

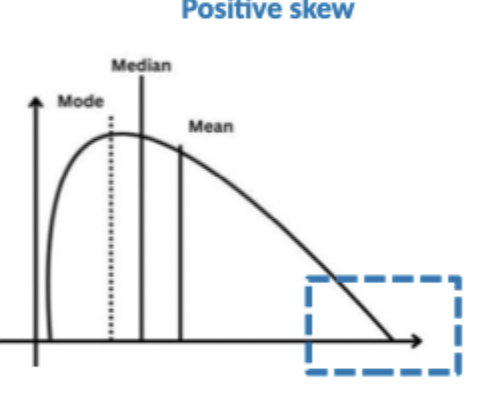
Describe postively skewed data distributiosn?

Right skewed, tail is longer on the right side of the peak, more data on the left, data is concentrated towards higher values

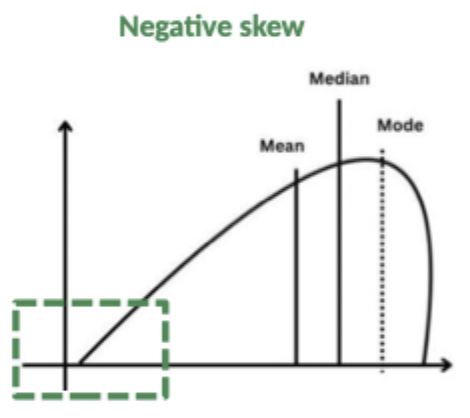
Describe negatively skewed data distribution?

Left-skewed, tail is longer on the left of the peak, more data on the right, data is concentrated towards the lower values

What is Kurtosis?

The shape/ the ‘tailedness’ of a distribution e.g. heavier or lighter tails

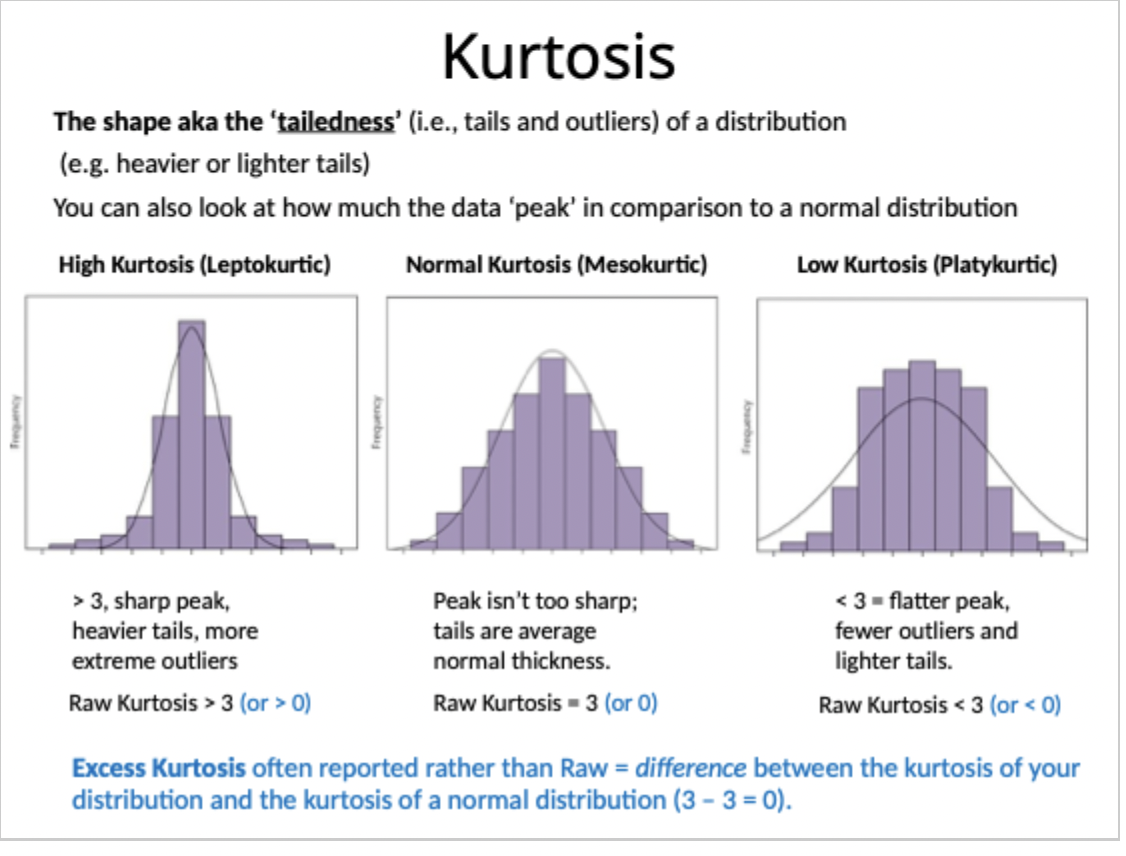
What is excess kurtosis?

often reported rather than raw = difference between the kurtosis of your distribution and the kurtosis of a normal distribution

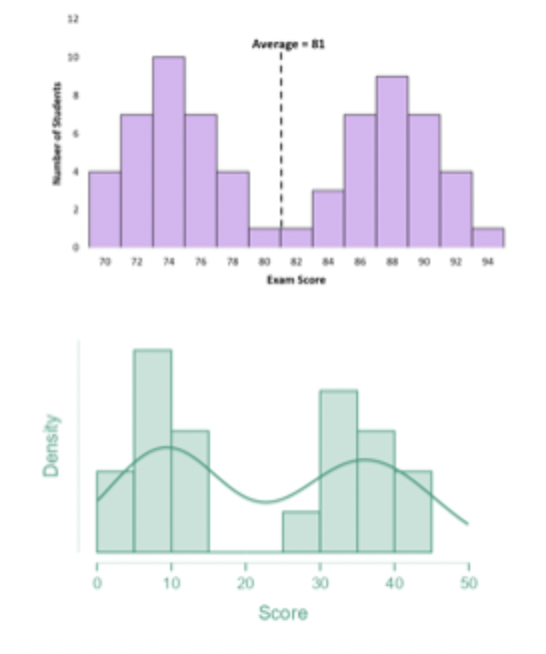
What is a Bimodal Distribution?

• Two clear peaks

• Or two clusters/dominant groups

• typically occur when data come from two different groups

• or indicate sub-populations in the data

• requires careful interpretation

What is Uniform Distribution?

• Flat shape

• No peak, more rectangle shape

• al values equally or relatively likely to occur with similar frequency

• values are spread evenly across a fixed range

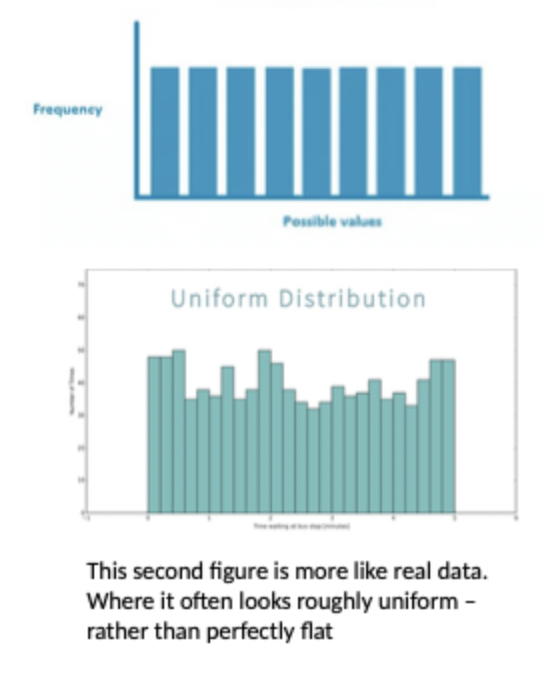
What is the deference between dispersion and distribution of data?

• distribution of data answers what daya looks like overall i.e. shape, centre, spread

• dispersion answers how wide or narrow that distribution is, i.e. the width/spread of data, specific numbers (like standard deviation, variance, IQR) that quantify how spread out that data is around its center, indicating variability or consistency

What happens to the distribution of data of there is a small SD?

Data os clustered around the mean, curve becomes narrow and taller

What happens to the distribution of data when there is a large SD?

data is more spred our; curve becomes wider and flatter

Comparison summary of distribution types:

Why does distribution matter?

• Understanding the sape is crucial data for inference

• this is for accurate predictions and hypothesis testing

What are parametric tests?

Inferntial/statistcal tests that assume data have normal distributions

What happens in inferential tests when distribution is non-normal?

you may need to:

• transform the data

• use a non-parametric test

what is homogeneity of variance?

Inferential tests that assume the varian/dispersion is similar across groups

If variance is greatly different between different groups rather than similar what does this indicate?

• Your tests may not be valid

• you may have use adjusted / corrected tests or on-parametric tests

Why is having a normal distribution central to hypothesis testing?

it acts as the foundation: to understand how scores relate to one another within a distribution and across disributions - to predict and standardise scores so we can compare different populations or different measures

What are Z-scores?

• standardised values showing how many SDs a data point is from the mean

• calculated by the mean/centre of distribution and the width/spread of the data

• tells us exactly where in the standard normal distribution a value is located

what Z-scores allow for?

• Allow comparisons within the dataset - sample distribution to help interpret values or detect unusual values

• OR allow comparisons across different datasets

• OR to a theoretical population distribution

• Z-scores are calculated assuming a normal distribution

How does a normal distribution help predict where most scores will fall?

• The normal curve represents probabilities

• are under the curve = 1 or 100%

• centred at 0 (increments of 1)

• The tails are rare events (extreme values)

• in the standard normal distribution the z-axis shoes z-scores

What does a Z-score tell you about a raw score?

• Magnitude value - size in standardised unites of the difference/distance from the mean/centre

  • Larger than z-score = more rare (smaller probability)

  • Generally, fall between - 3 and 3

• Location - which half of the distribution is the raw score sitting. Denoted by a sign (positive or negative)

  • Positive Z-score = above the mean, to the right

  • Negative Z-score - below the mean , to the left

whats a Z-statisitc?

used to report the actual results of analysis tests

What does a Z-score of -1 tell us?

That a score is 1 standard deviation away from the mean. As the sign is negative it means its below the mean so to the left.

Formula to calculate z-scores

Z = raw data/observed score - population mean / population standard deviation

Z-score calculation example

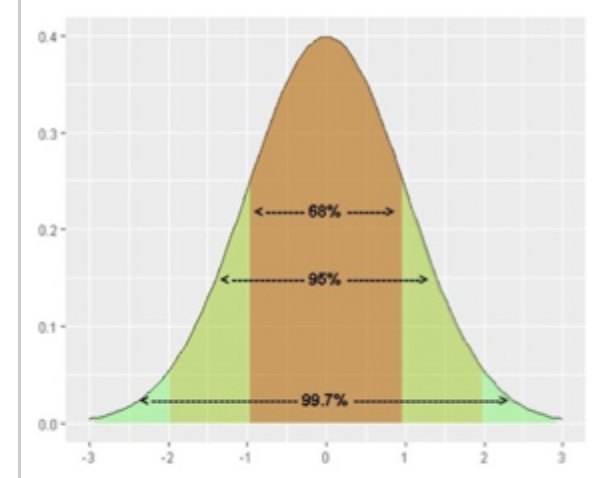
What is the Empirical Rule?

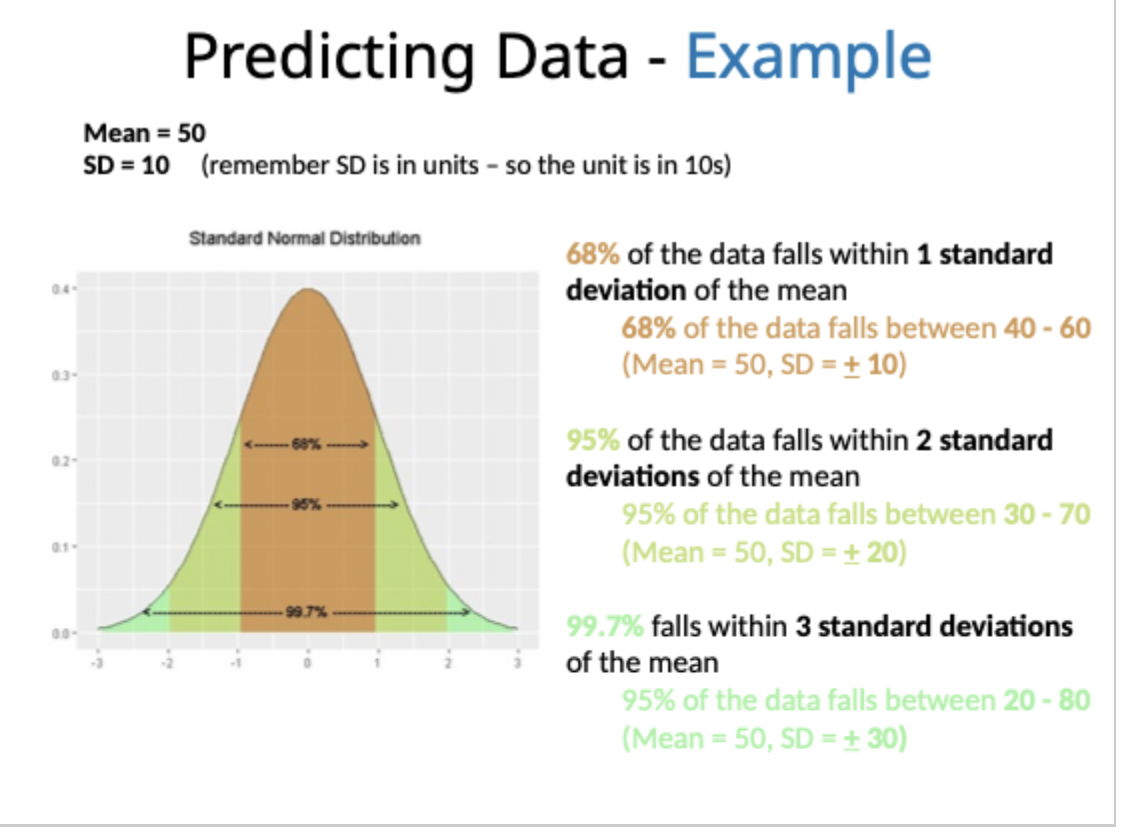
• 68% of the data falls within 1 standard deviation og the mean

• 95% of data falls within to 2 standard deviations of the mean

• 99.7% falls within 3 standard deviations of the mean

• the further out you go from the mean the less typical the score

Predicting data example

Why are Z-scores important?

• Gives the relative location of the persons score within its distribution

• see if a score is unusual or typical, even if two datasets are very different

• make meaningful comparisons - across datasets

• quantifies the difference between the raw data and what is expected

• transform non-normal distribution to a ormal distribution - convert scores into z-scores

• detect outliers / extreme values

How do you calculate a z-score if data are completely ‘non-normal’?

• transform the data to get approximate normality

• instead, use specific analysis tests (non-parametric tests)

• use percentile ranks instead of z-scores for interpretation

Why could data be Non-normal?

1. Outliers: data point that differs significantly from other observations

2. Insufficient data: sample size too small

3. Multiple distributions: bimodal

4. Measurement issues