L5: Subset selection and shrinkage methods

Linear model

Linear model has advantages with interpretability and good predictive performance

Advantages:

• Inference

  • Competitive to non-linear models

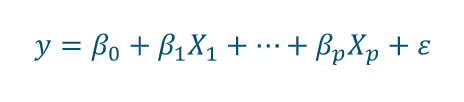
Prediction accuracy

True relationship linear, MLR low bias

Ratio p and n is important

n »p : low variance

n ~p: high variance, overtraining

n <p: no unique model (variance infinite)

Interpretability

Not all variables are associated with the response

By removing irrelevant features (set coefs to zero)

→ more easily interpreted, feature selection

Three alternatives to least squares

Subset selection

Shrinkage

Dimension reduction

Subset selection

Identify a subset of predictors that best predicts a response. Use least squares to fit the model

Shrinkage

Fit a model using least squares but shrink the coefficients to zero. This reduces variance and can perform variable selection

How to select subsets

Best subset selection

Fit separate least squares regression model

• For each possible combination of predictiors

  • model with 1,2, .. p predictorss

How to select single best model?

Select best model out of p+1 models

RSS decreases monotonically, R² increases monotonically

RSS/R² is a bad choice

• will end with max variables in model

RSS/R² is about training error

Choose model with low test error

• Cross validation or some other criterion

  • Cp, AIC, BIC and adjusted R²

• Best subset selection is unfeasible for p > 40

same logic for best subset also extends to other models

• logistic regression

Forward stepwise regressoin

Computationally efficient alternative

start with an empty model

• keeps on adding predictors one-at-a-time that gives best additoinal improvement

Cost - how many models

Best subset selction: 2^p models

Forward stepwise selection:

• One null model

• p=k models in the Kth iteration (k=0, …, p-1)

Backward stepwise selection

Starts with full least squares model containing all predictors

Iteratively removes least useful predictor one at a time

like forward, 1 + p(p+1)/2 models

n>p (must be)

Hybrid approaches

Combination of forward selection and backward elimination

Idea is to remove a variable added by forward when it no longer improves the model fit

Choosing the best model

Select the best model amongst models with different number of predictors

Training error estimates R², RSS are not suited

Best model: model with smallest test error

Two common approahces

• make adjustment to training error

  • Cross validation

Cp, AIC, BIC and adjusted R²

Training error MSE is underestimate of test MSE

Adjust training error for model size

• can be used to select between models with different numbers of variables

Four criteria

• Mallow’s Cp, colin lingwood mallows

• AIC, Aikake information criterion, hirotugu aikake

• BIC (Bayesian information criterion)

• Adjusted R²

Cross-validation

K-fold cross validation

Leave-one-out cross validation

Advantage over AIC, BIC, Cp and AdjR^@

• Provides a direct estimate of test error

• Fewer underlying assumptions

  • Useful in wider range of model, e.g. hard to estimate estimate of error varaince

One-standard-error-rule

Select smallest model for which test error is within one standard error of the lowest point

Shrinkage methods

Subset methods use least squares to fit a model using a subset of predictors

Alternatively, we can fit all predictors using a technique that constrains or regularizes the coefficient estimates

• shirnks the estimates to zero

Shirnking coefficients reduces their variance

• best known methods: ridge regression and lasso

  • q

Ridge regression

As with least squares, ridge regression seeks coefficient estimates that fit the data well, by making the RSS small

However, the second term (shrinkage penalty) is small when beta1, … beta p are close to zero and thus it has the effect of shrinking the estimates of Betaj towards zero

The tuning parameter lambda serves to control the relative impact of these two terms on the regression coefficient estimates

Lmabda

when lambda = 0, penalty has no effect, ridge produces least squares estimates

when lambda → infinity, impact of penalty grows and coeffiicient will aproach zero

Selecting a good vaue for lambda is critical

• cross-validation is used for this

scaling of predictors

The standard least squares coefficient estiamtes are scale equivariant

• multiplying Xj by a constant c simply leads to a scaling of the least squares coefficient estimates by a factor of 1/c

In contrast, the ridge regression coefficient estimates can change substantially when multiplying a given predictor by a constant, due to the sum of squared coefficients term in the penalty part of the ridge regression objective function

Therefore, it is best to apply ridge regression after standardizing the predictors

Why does ridge improve over least squares

Ridge regression is an "improvement" because it accepts a tiny bit of bias (not fitting the training data perfectly) in exchange for a massive reduction in variance (making better predictions on new data). Variance is the error that comes form being too sensitive to small fluctuations in the training set

In data science, we almost always prefer a model that is "mostly right all the time" over a model that is "perfectly right once but wrong everywhere else."D

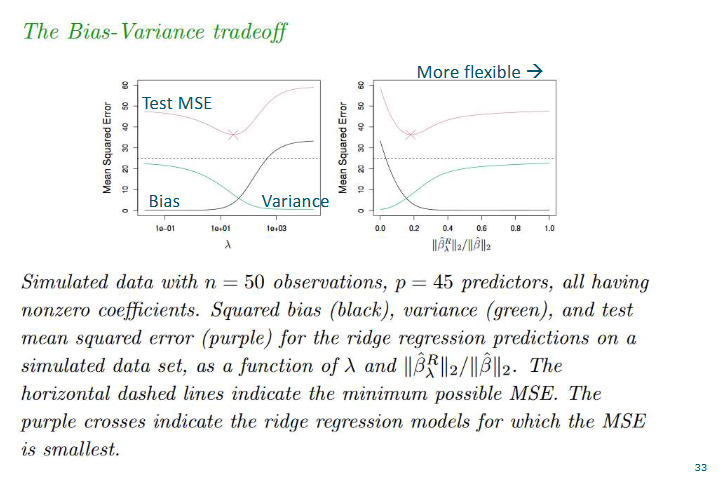
Drawback of ridge regression

It will include all p predictors, no selection

• None of the regression coefficients will become exact zero

• Not a problem for model accuracy

  • A problem for model interpretation

The Lasso

Lasso also shrinks coefficients to zero, but this time they can become zero

Models have fewer predictors, thus easier to interpret

Lasso performs variable selectionV

Variable selection properties of Lasso

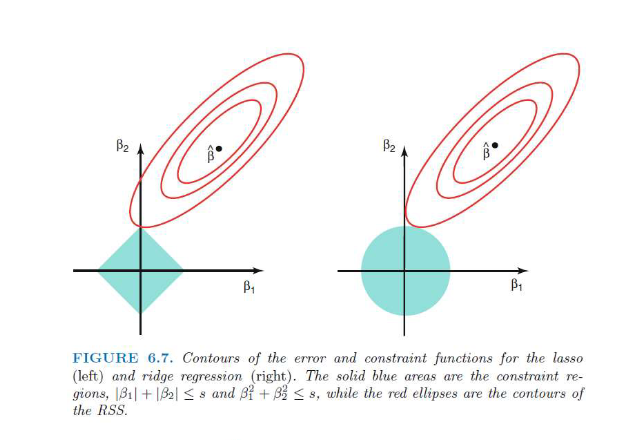
1. The Shapes: The "Constraint Regions"

The blue areas represent the "budget" or limit placed on the coefficients ($\beta_1$ and $\beta_2$). The penalty parameter $\lambda$ (or $s$ in this diagram) determines how small these shapes are.

• Lasso (The Diamond): Because Lasso uses absolute values ($|\beta_1| + |\beta_2| \leq s$), the boundary is a diamond. In 2D space, absolute values create straight lines that meet at sharp corners on the axes.

• Ridge (The Circle): Because Ridge uses squared values ($\beta_1^2 + \beta_2^2 \leq s$), the boundary is a circle. This is the standard equation for a circle centered at the origin.

2. The Red Ellipses: Residual Sum of Squares (RSS)

The red rings are like a "topographical map" for error.

• The black dot ($\hat{\beta}$) in the center is the Least Squares estimate (the point of minimum error).

• As you move away from that dot, the error (RSS) increases. Every point on a single red ring has the exact same error level.

wHat is better, ridge or lasso?

Depends on data characteristics

Lasso assumes some predictors are not related to the response

Ridge includes all predictors in the model

Selecting the tuning parameter

As for subset selection, for ridge regression and lasso we require a method to determine which of the models under consideration is bets

That is, we require a method selecting a value for the tuning parameter lambda, or equivalently, the value of the constraints

Cross-validation provides a simple way to tackly this problem. We choose a grid of lambda values, and compute the cross-validation error rate for each value of lambda.

We then select the tuning parameter value for which the cross-validation error is smallest

Finally, the model is re-fit using all of the available observations and the selected value of the tuning parameter