Georeferencing a Raster

Why do you need to georeference a raster?

• We have a spherical coordinate system for anything that is global scope and the raster is 2d

• have to standardize the GIS data set to the rules that are needed for the presentation or solution

• allows for coordinate transformation

What to do to a gis raster data set that is not georeferenced?

If any data set is missing a spatial reference and you now what it should(i.e., from the meta data) be use the define projection toll and fix it

What about projecting rasters?

• use the project raster tool

• project onto the extent(like using the create features tool). Then make estimate on what the cell size will be. The size of the pixel will be the same but the area it is representing will differ a bit, which causes a bit of distortion.

  With the x and y coordinated do not add that many (1 max) decimals

• then use fishnet tool to make the raster graticules

• The problem with a raster is that our attribute are tied to whatever our pixel system is.

• So we have to determine what values, and find a way to fill in the values

Resampling

Happens : during projections, and geometric transformations, georeferencing control points(need to do on the lad next week)

we have the empty matrix of cells and you have to consider how to repopulated them.(type) Nearest neighbor resamples; what goes into the output is whatever values is closes measuring from cell center to center

 

during the georeferencing process(from one cell size to another) can happen. Will take either the minimum or maximum before boolean functions, it happens everywheren in raster analysis\

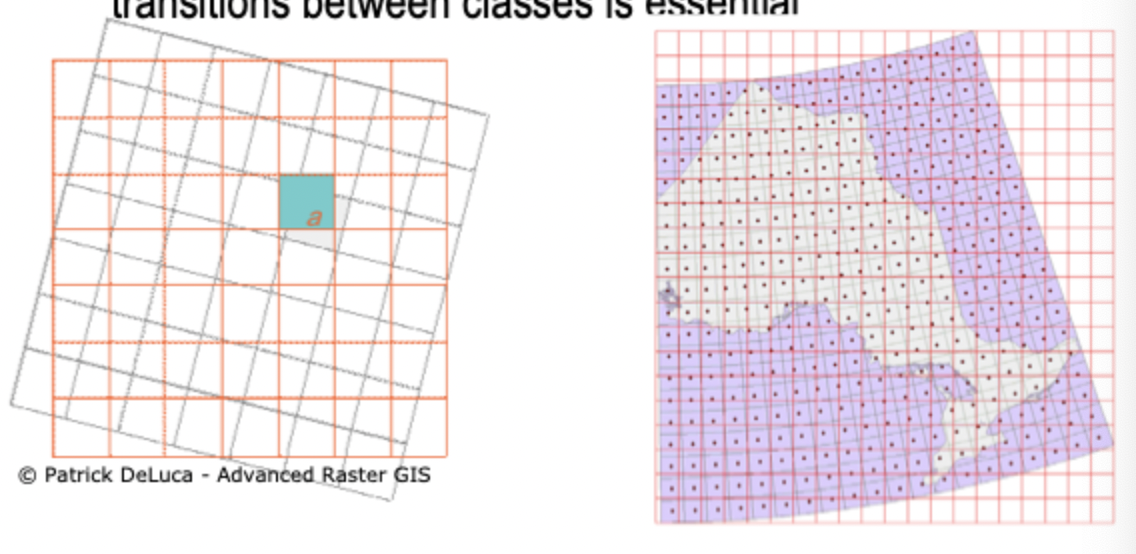
Resampling technique: Nearest neighbour

• values in output are assigned based on the nearest neighbour in the input raster

• use it on categorical grids, where maintaining sharp transitions between classes is essential

Will not alternate values in any way; Some data values will be lost and some will be duplicated, most often along the edges, and sensitive to noisy data

Pros:

• computational efficiency- straight forwards calculation=faster speed

• preservation. of data values

• no interpolation of values, so no intermediate values intorduced

Cons:

• blocky output(especially when changing resolution)

• some data values may be lost, while other duplicated

• sensitive to noisy data

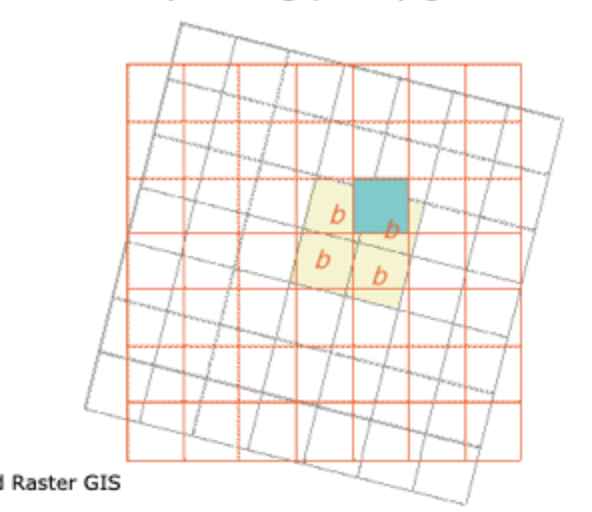
Re-sampling Techniques: Bilinear Interpolation

• cell values determined by calculating distance-weighted average of 4 closest input cells

• used on continuous(floating point) grids

Pros:

• smoothing affect compared to nearest neighbour

• balance between computational efficiency and visual quality

• preservation of edges

Cons:

• limited accuracy for non-linear surfaces

• can smooth over sharp features

• sensitives to nosie

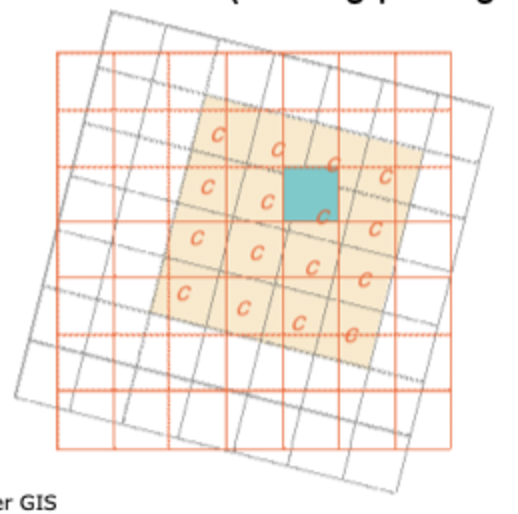
Re-sampling Techniques: Cubic Convolution

• output cell values determined by calculating the distance weighted average of the closest 16 input calls

• used on “noisy'“ continuous (floating point grids)

Pros:

• smother looking image than bilinear and nearest neighbour

• greater preservation of sharp features

• suitable for up-sampling

Cons:

• computational intensity makes it slower than nearest neighbour or bilinear interpolation

• potential for overshooting- interpolated values exceed the range of the original data

Re-sampling Techniques:Majority

• bases on most common vales within 4×4 window

• use it on Categorical (integer) grids

Pros:

• preservation of dominant features

• minimization of noise impact

Cons:

• disregard for minority categories
  

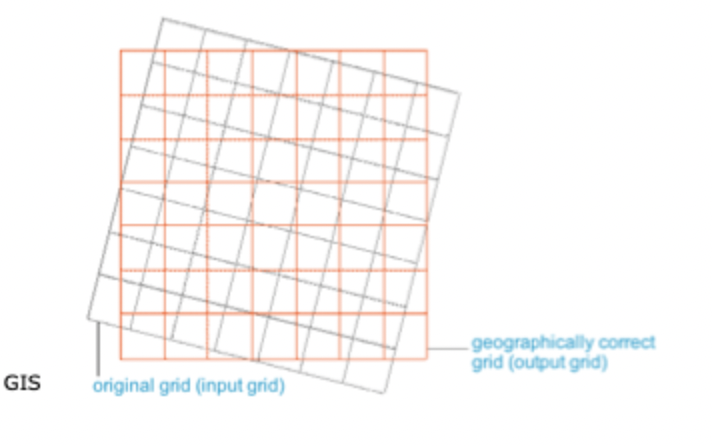
How to Georeference a Raster Without a CS Steps

• aligning the raster with control points to spatially referenced data

• transforming the raster into the new coordinate space

• resampling

• persisting the georeferenced data set

Vector will have  a pcs, the raster is missing, you will load the vector data set then add the raster that is missing, then align them with control points

Then you have to resample\and the persisting of the data set

Control Points

Used to build polynomial transformation that will shift a raster dataset from its existing location to the spatially correct location

based on know coordinates or identifiable locations

number of points based on complexity of transformation(usually 3 minimum)

• more points does not mean more accuracy

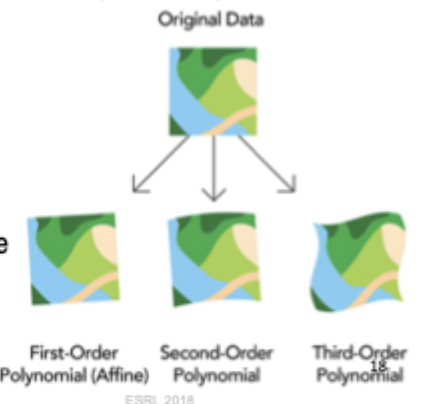
Choices for Geometric Transformation: Polynomial

• built on control points and least squares fitting

• optimized for global accuracy, potentially poor local accuracy

• (want the points spread out, so the registration is not inaccurate)

• number of control points needed

  • 0- for zero order

  • 3 for first order.

  • 6 for a second order

  • 10 for a third order

• Usage

  • first order (affine)- stretch, scale, rotate

  • second and third order- bend curve

Choices for Geometric Transformation: Spline

• a true rubber sheeting method

• optimizes for local accuracy but not global accuracy

• transforms the source control points exactly to target control points

  • the pixels that are distance from the control points are not guarantees to be accurate

  • thus transformation is useful when the control points are important, and it is requires that they be registered precisely i.e., survey markers of data markers

• spline requires a minimum of 10 control [points

Interpreting RMS Error

RMS

error represents the difference between the original control points and the new control point locations calculated by the transformation process

RMS error is a good assessment of the transformation of the transformation process

don’t confuse a low RMS error with an accurate registration

• spline transformation give an RMS of zero; however, this does not mean that the image will be perfectly georeferenced