Chapter 17 - Oscillations

physics y2, module 5

17.1 intro

the examples of oscillating motion include a simple pendulum, the end of a ruler hanging over the edge of a desk, or a volume of water in a U-shaped tube, but all share similar characteristics, what are they?

• in each case the object starts in an equilibrium position

• a force is then applied to the object, displacting it, and it begins to oscillate

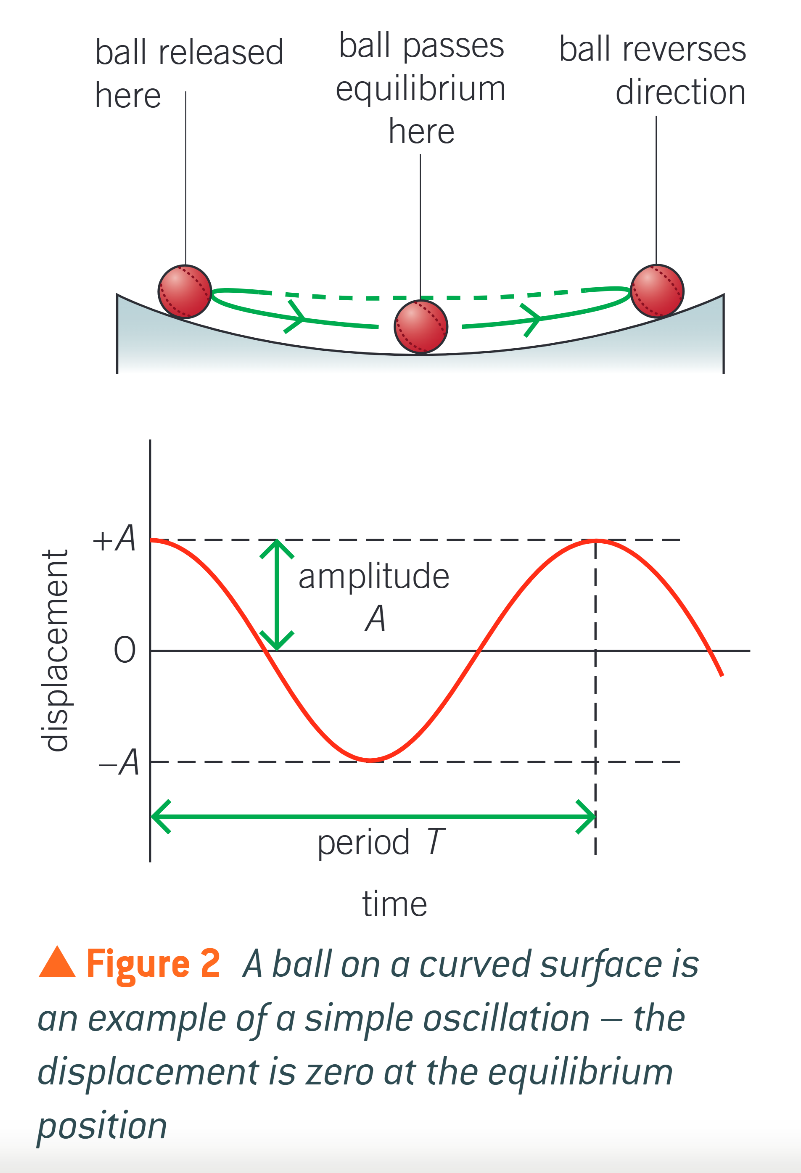
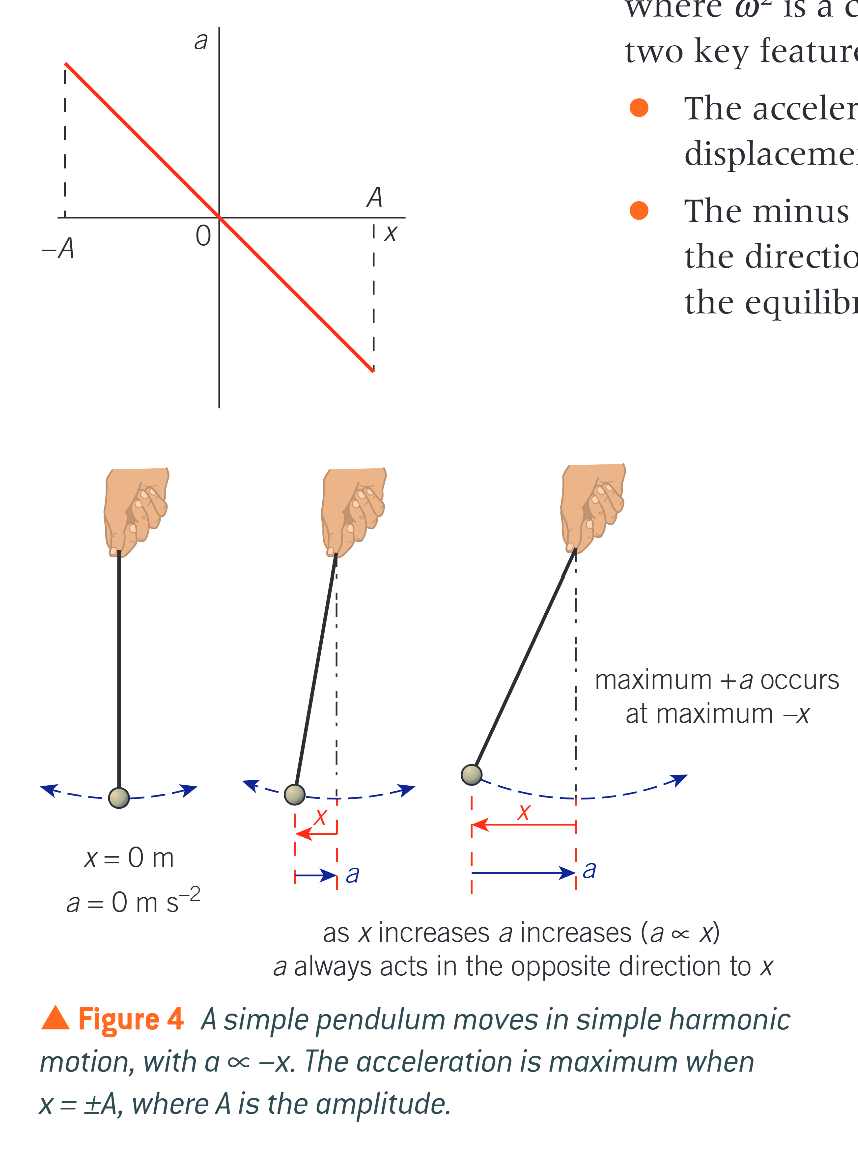
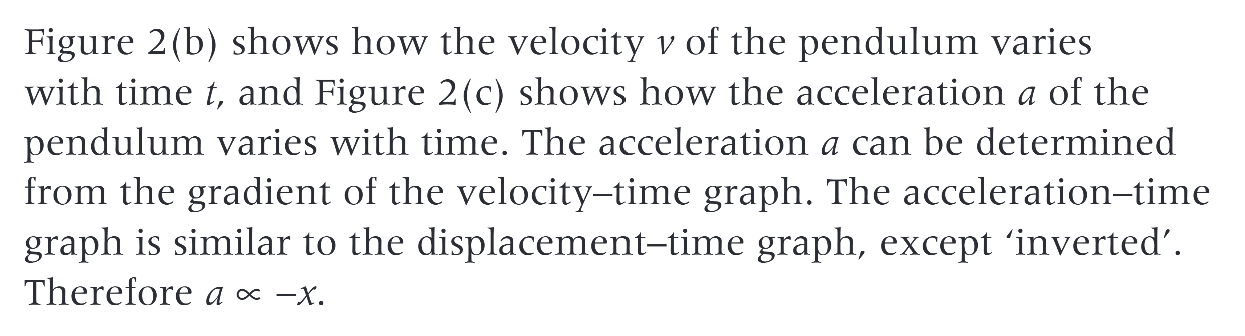
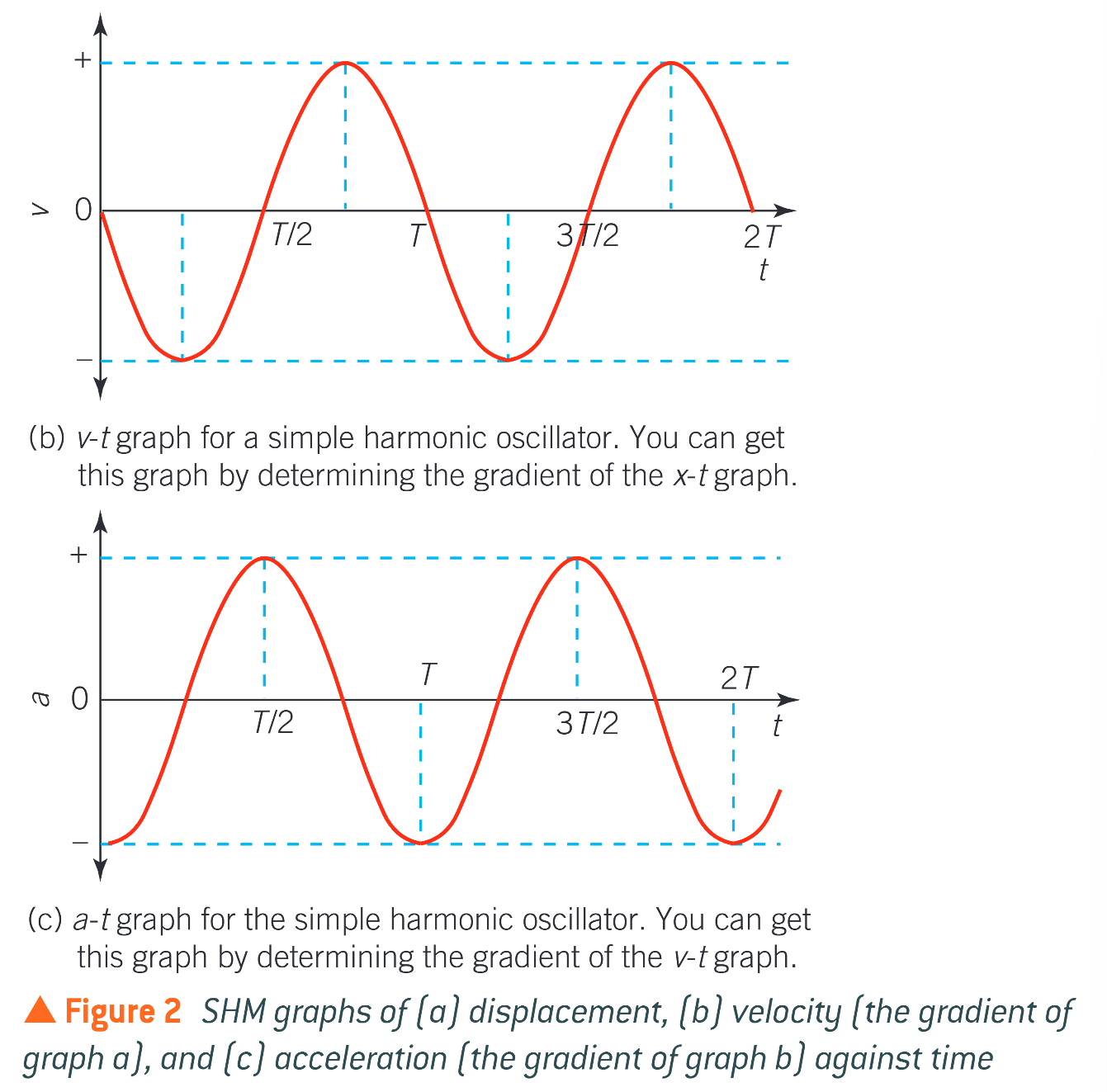
how does figure 2 work, when an object displaced from its equilbrium position is released

• it travels towards the equilibrium position at increasing speed

• it slows down once it has gone past the equliibrium position, eventually reaching maximum displacement (amplitude)

• it then returns towards its equilibrium position, speeding up, and once more slows down to a stop when it reaches negative displacement

• this motion is repeated over and over again

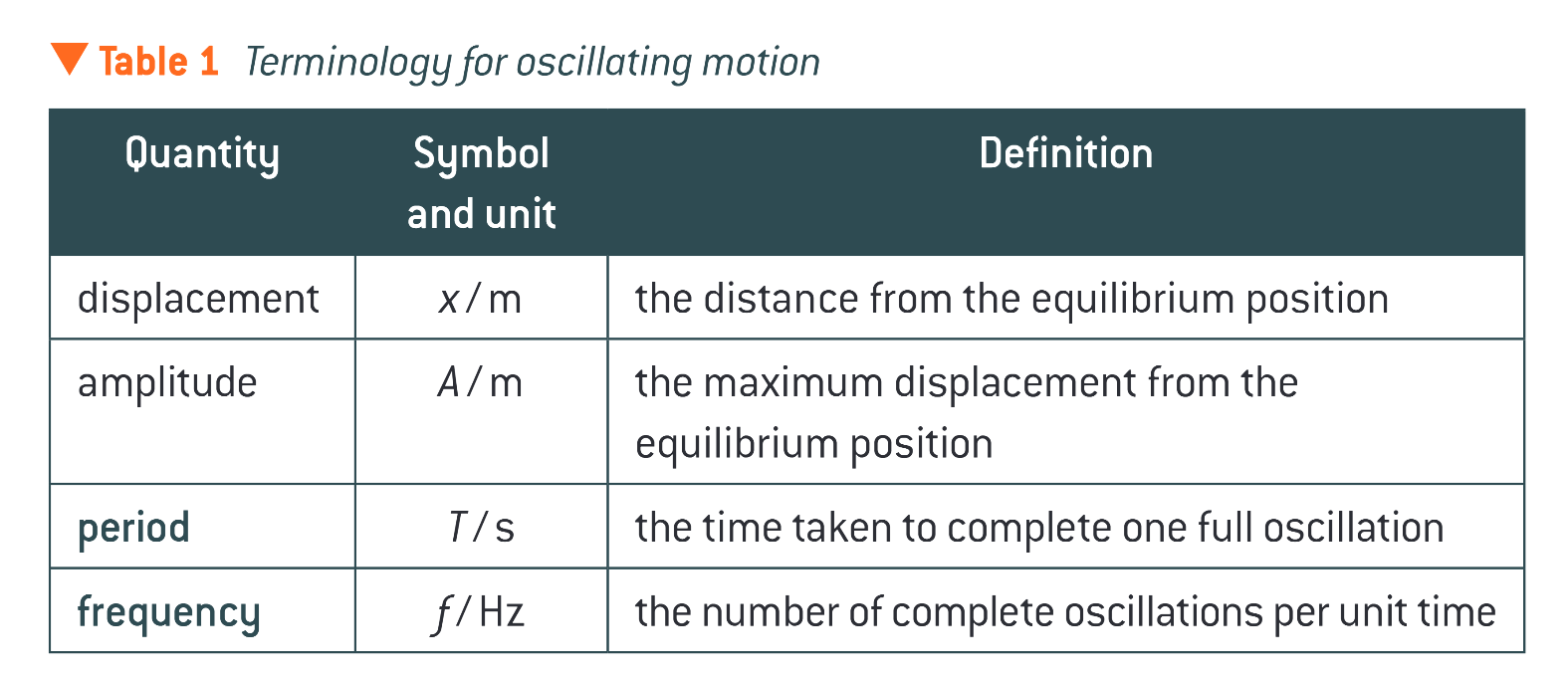
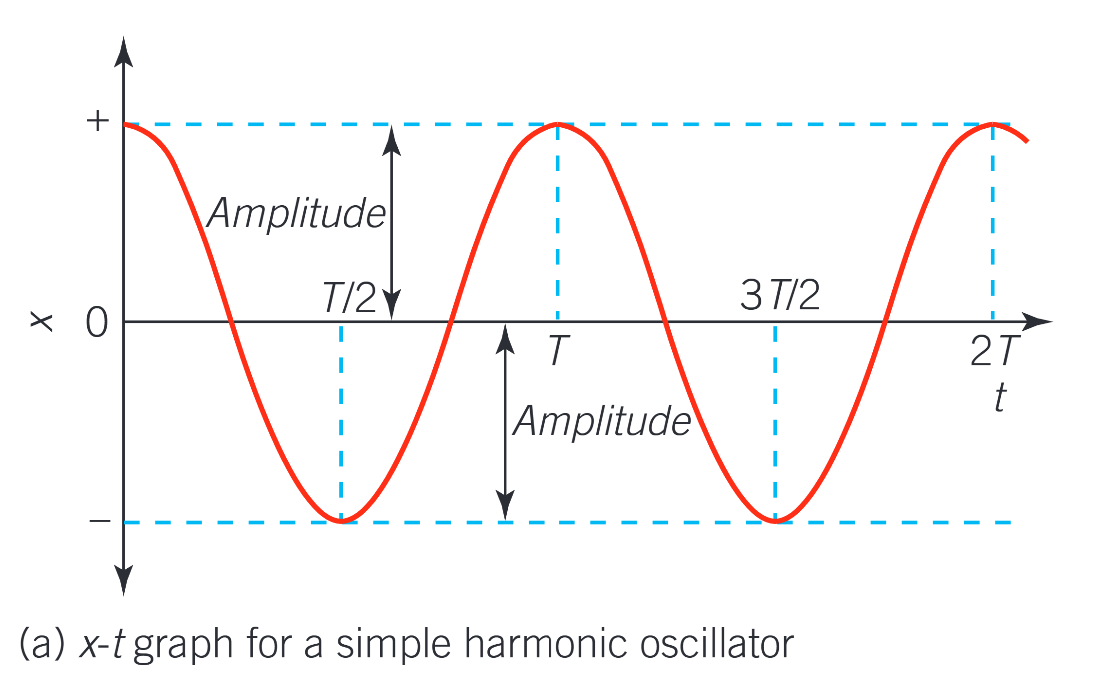
displacement definition and symbol and unit

amplitude definition and symbol and unit

period definition and symbol and unit

frequency definition and displacement

Angular frequency

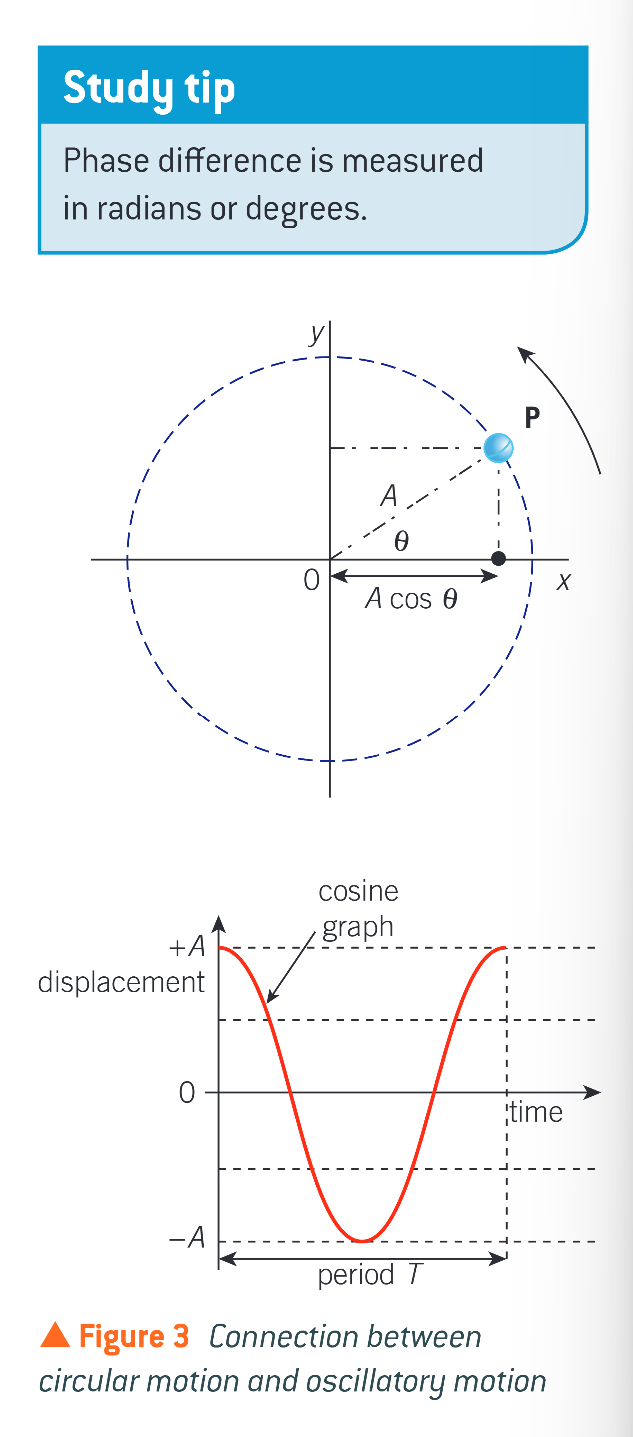
what is angular frequency

a term used to describe the motion of an oscillating object and is closely related to the angular velocity of an object in circular motion

the angular frequency of an oscillating object is given by the 2 following equation, what are they?

what is an isochronous oscillator?

• the period T of the oscillator is independent of the amplitude A of the oscillator

• for example, the period of a simple pendulum moving in SHM does not depend on the amplitude of the swing

• As the amplitude increases, so does the average speed of the swing, so the period does not change

Worked example: frequency and maximum acceleration of a pendulum bob

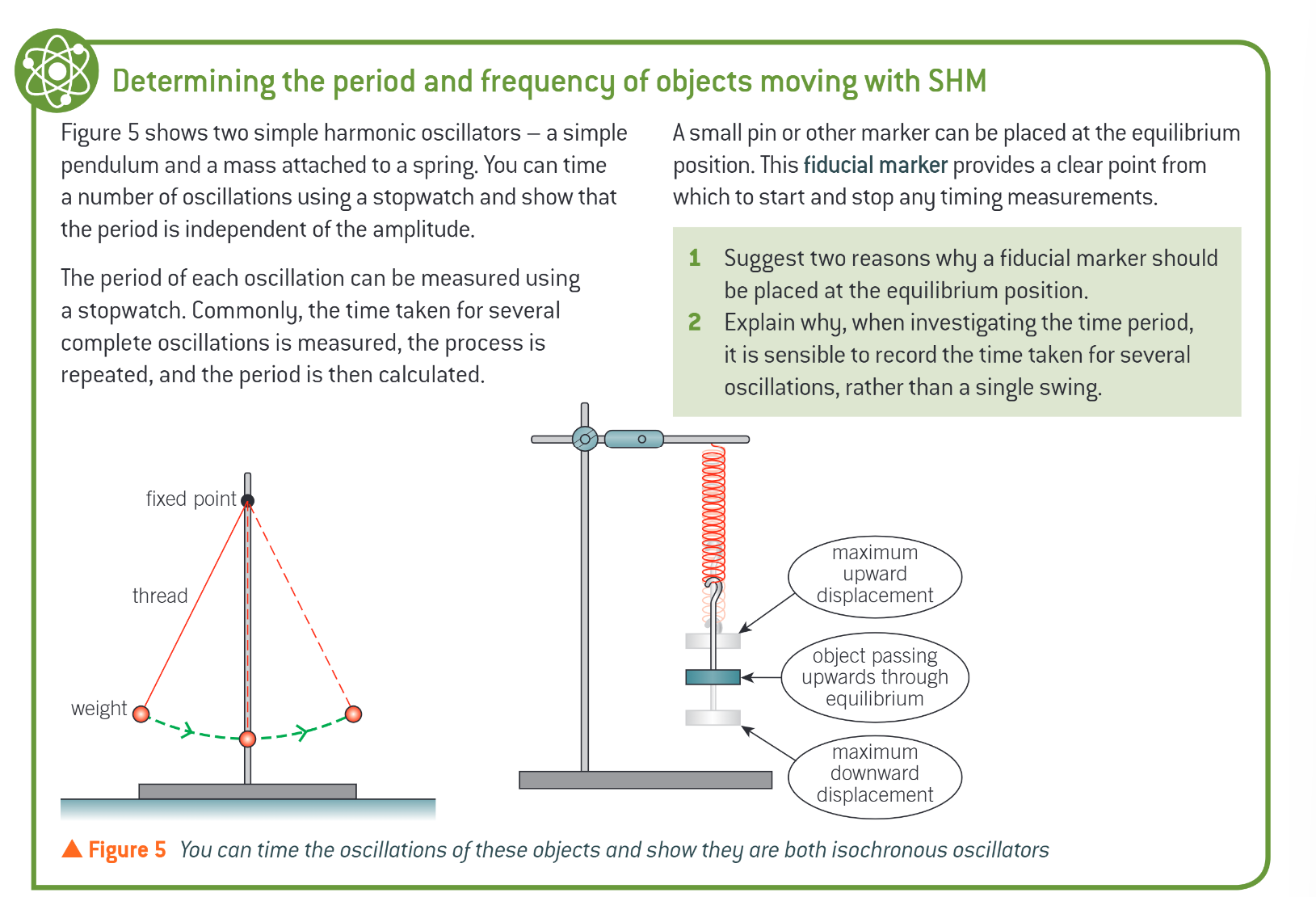
determining the period and frequency of objects moving with SHM

17.2 intro - analysing shm

what is the defining equation for SHM

worked example: the displacement of a simple pendulum

velocity

worked example: the velocity of an oscillating tray

17.3 intro - simple harmonic motion and energy

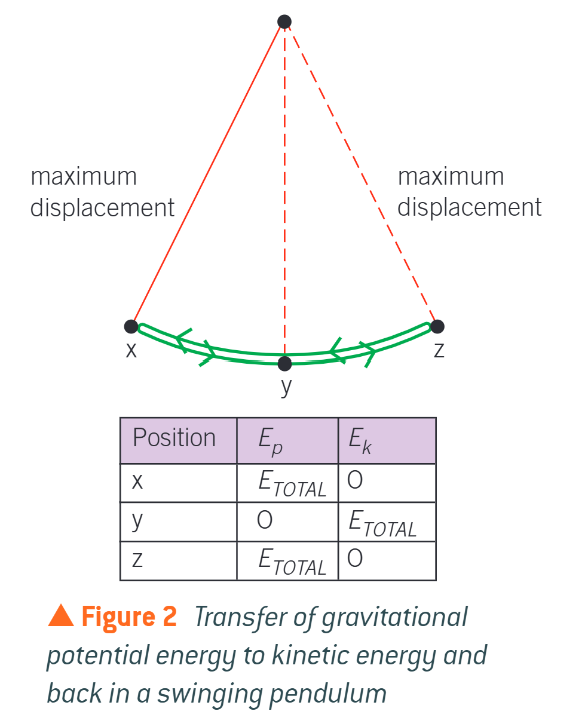
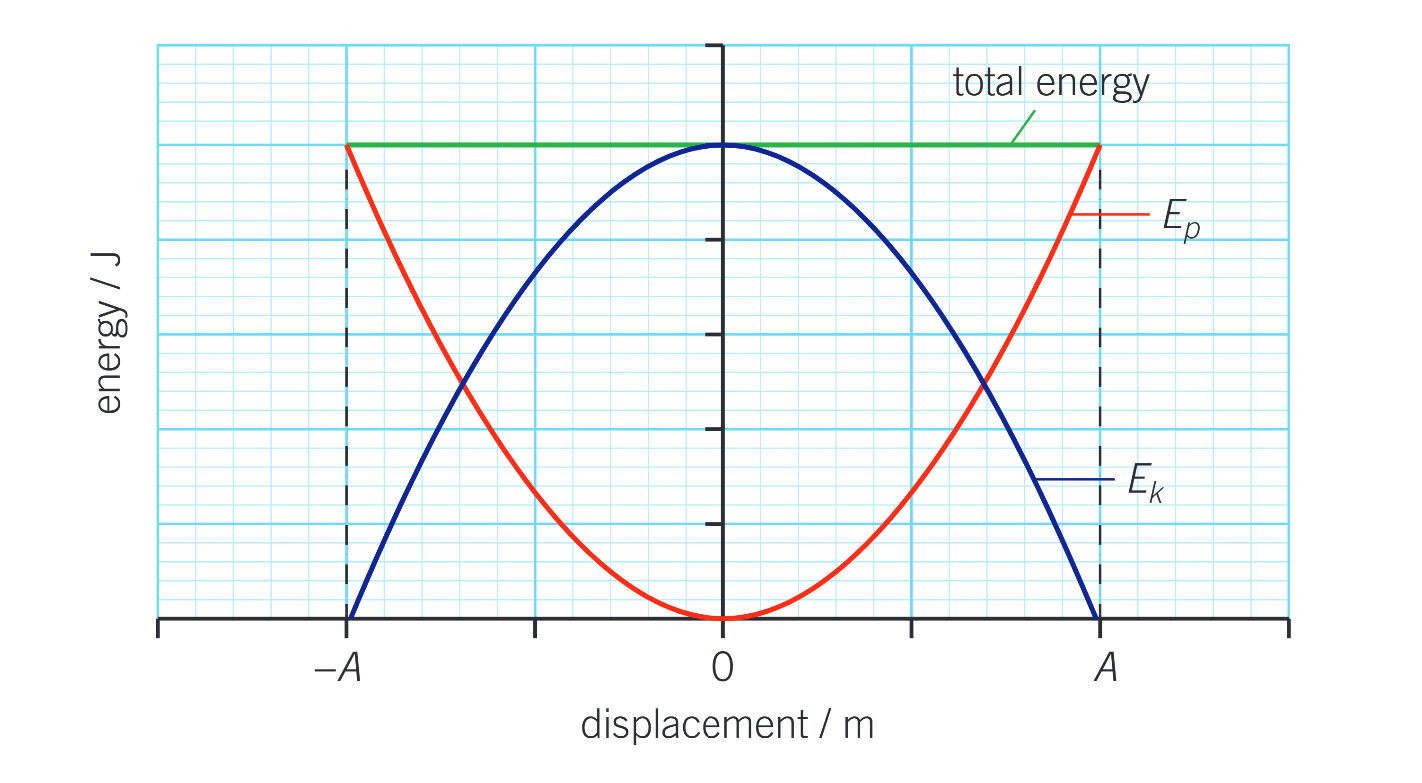
graphs of energy against displacement - for any object moving in SHM the total energy remains constant, as long as there are no losses due to frictional forces. Figure 2 shows the energy changes for a simple pendulum. Draw the graph and describe what is happening at each part of the graph

• at the amplitude the pendulum is briefly stationary and has 0 kinetic energy

• all its energy is in the form of potential energy (in this case, gravitational potential energy)

• as the pendulum falls it loses it potential energy and gain kinetic energy

• it has maximum velocity, and so maximum kinetic energy, as it moves through its equilibrium position

• as the pendulum passes through the equilibrium position, it has no potential energy

• the graph of energy against displacement shows how the total energy of an oscillating system remains unchanged (the green line in figure 3)

• there is a continuous interchange between potential energy Ep and kinetic energy Ek, but the sum at each displacement is always constant and equal to the total energy of the object

• the red line on the graph represents the potential energy, and is 0 at the equilibrium position

• the purple line represents the kinetic energy and is 0 at the amplitude

describe the interchange of potential energy and kinetic energy for a mass - spring system

if the mass is oscillating vertically, the potential energy is in the form of gravitational potential energy ( due to the position of the mass in the Earths’s gravitational field ) and elastic potential energy ( stored in the spring ). If the mass is oscillating horizontally, the potential energy is in the form of elastic potential energy only.

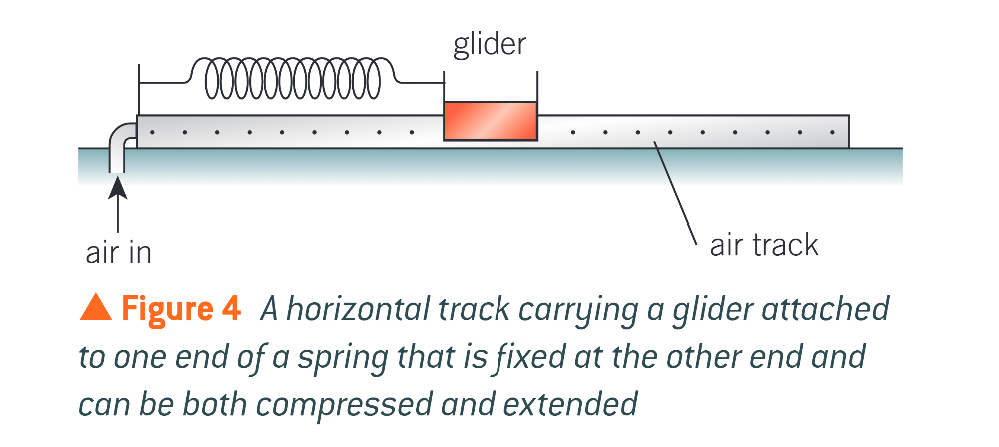
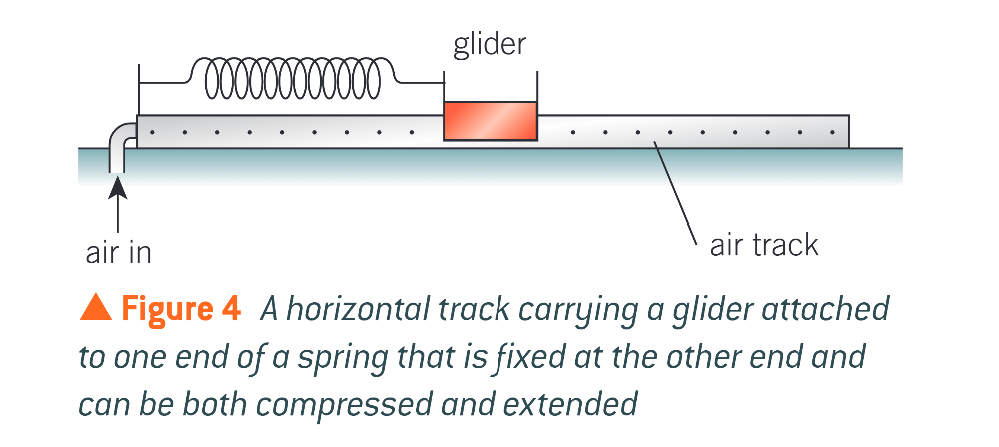
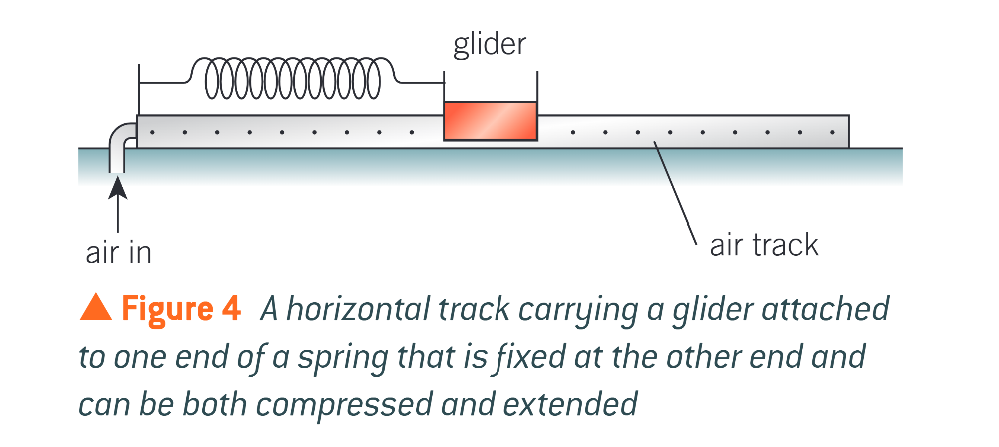
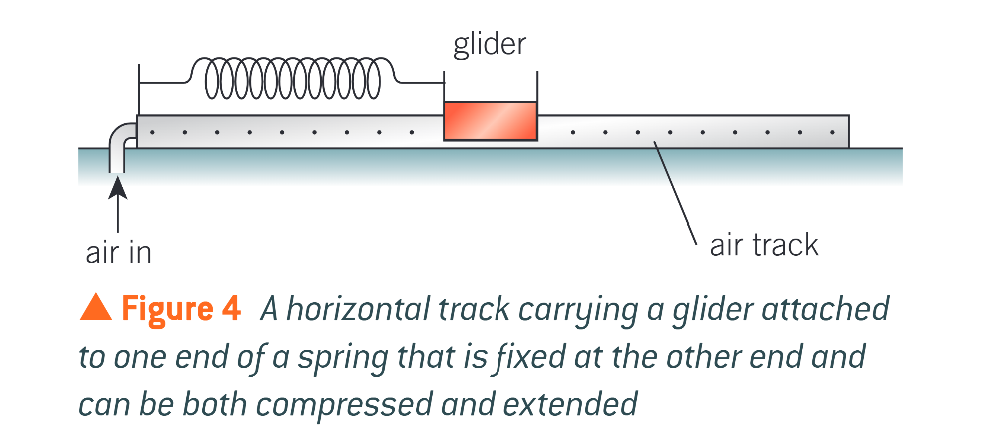
when displaced, the glider will move in?

SHM

what 2 forms of energy does the system have?

elastic potential energy in the spring and kinetic energy of the spring and the glider

the displacement x of the glider is the same as…?

the extension or compression of the spring

what equation is used for the potential energy Ep

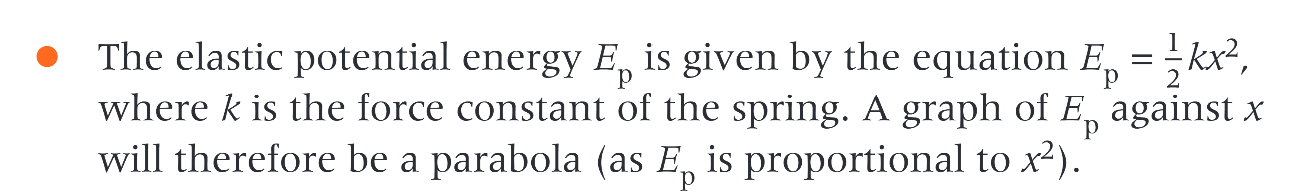
the elastic potential energy is always…

positive and varies from Ep=0 when x=0 to Ep=1/2kA² when x=A (amplitude)

what happens when x=A

the glider will be stationary for an instant. This means that it has no kinetic energy. The total energy of the oscillator must therefore be equal to 1/2kA²

the kinetic energy Ek of the glider at any instant must be?

the difference between the total energy and the elastic potential energy. Therefore… ( equation )

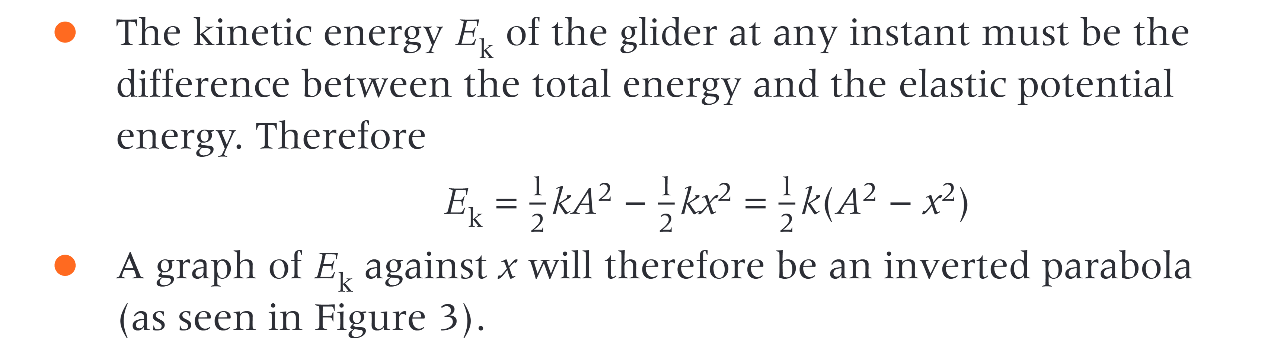
17.4 Damping and driving intro

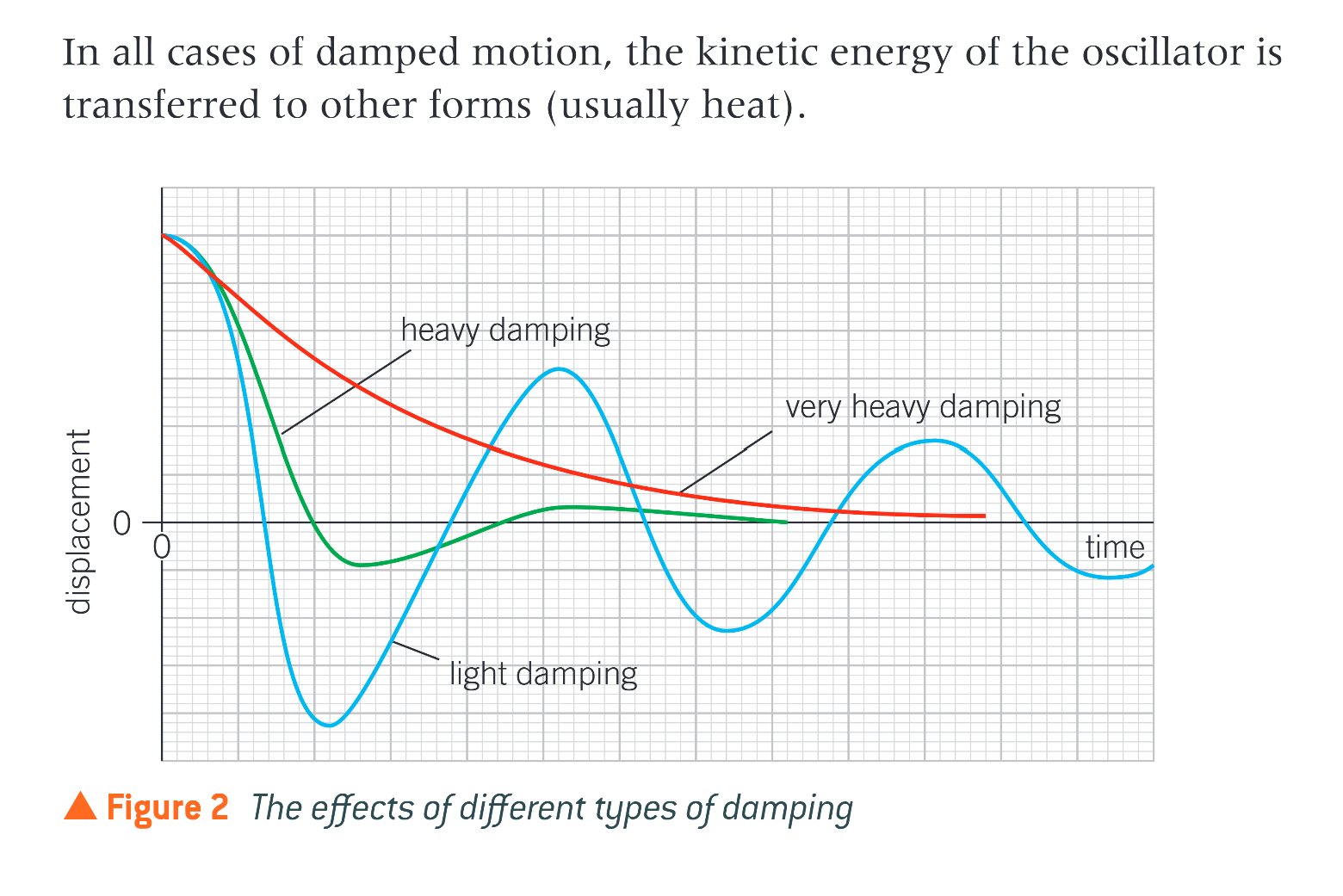
light damping

when the damping forces are small, the amplitude of the oscillator gradually decreases with time, but the period of the oscillations is almost unchanged. this would be the case for a pendulum oscillating in air

for larger damping forces, what happens to the amplitude and the period of the oscillations

• amplitude decreases significantly

• the period of the oscillations also increases slightly

example of heavy damping

a pendulum oscillating in water

now imagine an oscillator, such as a pendulum, moving through treacle or oil, what would happen

• in this example of very heavy damping, there would be no oscillatory motion.

• the oscillator would slowly move towards the equilibrium

what is free oscillation

when a mechanical system is displaced from its equlibrium position and is then allowed to oscillate without any external forces

what is the natural frequency

the frequency of the free oscillations

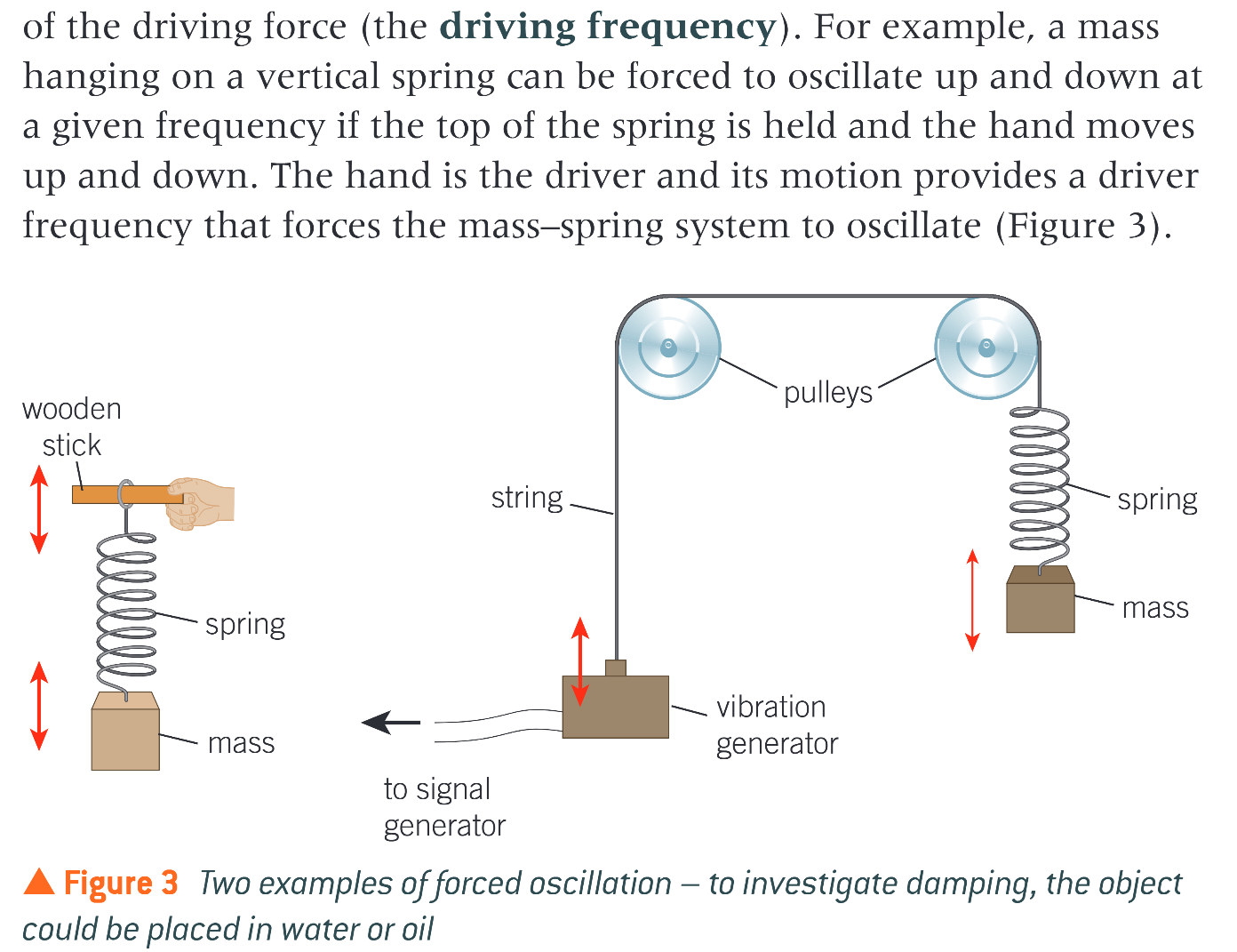
what is a forced oscillation

where a periodic driver force is applied to an oscillator

what is the driving frequency

the object will vibrate at the frequency of the driving force in a forced oscillation

if the driving frequency is equal to the natural frequency of an oscillating object, then the object will…

resonate

what will resonance do

this will cause the amplitude of the oscillations to increase dramatically, if it isnt damped, the system may break

Barton’s pendulums

17.5 Resonance intro

resonance is the effect that allows an opera singer to break a wine glass with just their voice

in the case of the wine glass, resonsance occurs when the frequency of the sound prouced by the singer is equal to the natural frequency of the wine glass

when does resonance occur

when the driving frequency of a forced oscillation is equal to the natural frequency of the oscillating object

for a forced oscillator with negligible damping, at resonance what is the equation

driving frequency = natural frequency of the forced oscillator

when an object resonates what happens to the amplitude of the oscillation

it increases considerably

if the system is not damped, the amplitude will increase to the point at which the object fails - the glass break, or the bridge collapses.

the greatest possible transfer of energy from the driver to the forced oscillator occurs at the resonant frequency. this is why the amplitude of the forced oscillator is maximum. in the case of the tacoma narrrows bridge, the kinetic energy from the win was efficiently transferred to the bridge, leading to its ultimate collapse