Sorting - Week 5

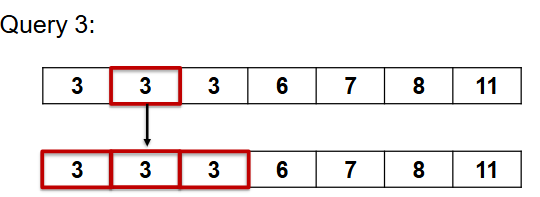
What is the complexity of this algorithm and why?

O(n²)

The outer for loop has a complexity of O(n) because you are going from 0 to n-1 numbers.

The inner loop has a complexity of O(n²) because the comparisons are: n+n-1+n-2+…+1 which = n(n-1)/2 (which is (n²/2 -n/2)).

Therefore the overall complexity is O(n²) because it grows faster than O(n)

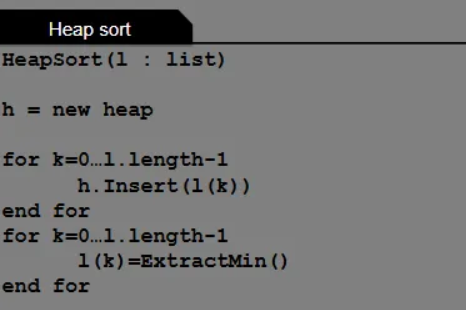
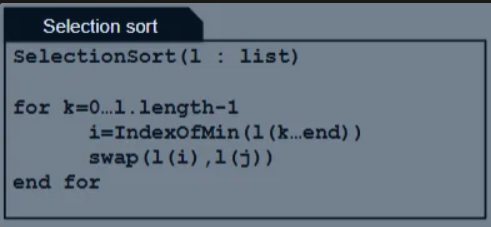
Why is the complexity for a heap sort O(nlogn)? Use the pseudocode to show

An implementation of SelectionSort, but uses a heap to get the smallest element.
→ Insert() in the first loop takes O(logn), hence this loop is O(nlogn).
→ ExtractMin() in the second loop takes O(logn) and so the second loop is O(nlogn).
→ Overall complexity of HeapSort is O(nlogn).

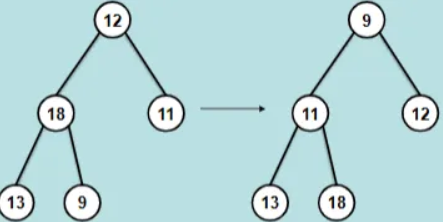
Using the list [12,18,11,13,9] how would a heap sort be performed

1. Build a binary tree from the array (list).

2. Transform the binary tree into a Min-heap.

3. Perform Min-heap sort:
   → Remove the minimum value in the sorted-array.
   → Restore the heap properly.
   → Repeat steps 4 and 5 until the heap is empty.

What is the complexity (worst-case time) for a quick sort?

If the pivot splits the list in exactly the middle, each sub-list is around half the size, so we would expect O(nlogn) complexity.

The lower list is size n - 1 and must be sorted.

It takes n recursive calls to QuickSort to finish sorting, each calling Partition which itself is O(n).

Hence QuickSort is O(n²), worse than MergeSort and HeapSort.

What is a quick sorts expected complexity and why?

→ The input is in an uniformly random order. Any element has equal chance to appear at any position.
→ Then our choice of the last element as pivot is equivalent to choosing a random element.
→ The expected complexity is O(nlogn), QuickSort recurses to expected depth O(logn) and executes O(n) operations.

Since the expected complexity of a quick sort is O(nlogn), the same as merge sort and heap sort, however it has an inferior worst case scenario - which is best?

The partition operations of QuickSort are in-place
with minimum swaps, so very efficient. Typically, it is several times quicker than the
others.

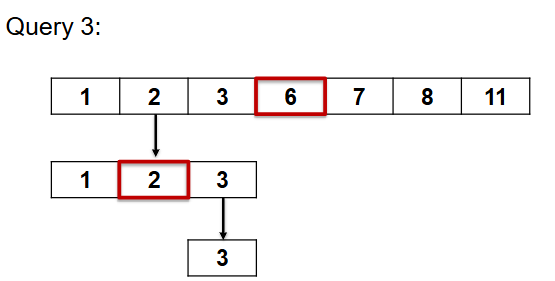
Applications of sorting - improved (binary) search

Compare the query with the middle item in the list.
If it is less, search the first half
If it is greater, search the second half
This is Binary Search O(logn)

Applications of sorting - improved search for number of occurances

To find the number of occurrences of an item x, first
search for the item in 𝑂(log 𝑛) time.
Then scan the list locally – all occurrences of x will
be next to each other.
This takes 𝑂(log 𝑛 + 𝑐) where c is the number of
occurrences.