MCAT Physics

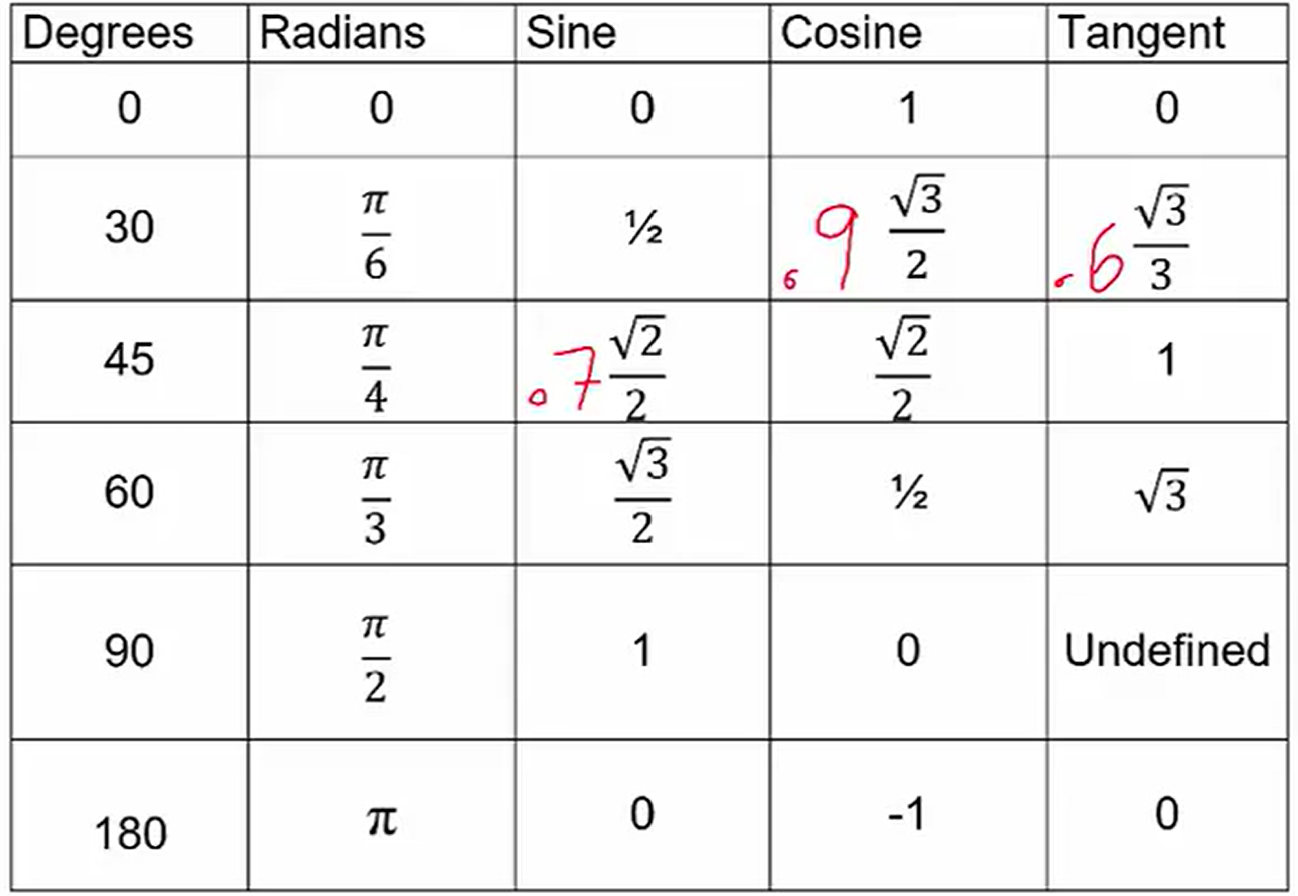
Degrees - Radians - Sine - Cosine - Tangent

SOH CAH TOA

Sine = Opposite / Hypotenuse

Cosine = Adjacent / Hypotenuse

Tangent = Opposite / Adjacent

Two Special Right Triangles

45-45-90

30-60-90

The 45-45-90 Triangle

1 - 1 - sqrt(2) triangle for the lengths of the sides

sin(45) = sqrt(2) / 2 = cos(45) [both the same]

tan(45) = 1

If theta < 45, then tan(theta) < 1

If theta > 45, then tan(theta) > 1

The 30-60-90 Triangle

1 - sqrt(3) - 2 triangle for the lengths of the sides

sin(30) = ½ ; cos(30) = sqrt(3) / 2 ; tan(30) = sqrt(3) / 3

cos(30) > sin(30) and tan(30) < 1

sin(60) = sqrt(3) / 2 ; cos(60) = ½ ; tan(60) = sqrt(3)

cos(60) < sin(60) and tan(60) > 1

Decimal Approximations:

sqrt(2)

sqrt(3)

sqrt(3) / 3

sqrt(2) / 2

sqrt(3) / 2

sqrt(2) = 1.4

sqrt(3) = 1.7

sqrt(3) / 3 = 0.577

sqrt(2) / 2 = 0.7

sqrt(3) / 2 = 0.866 = 13/15

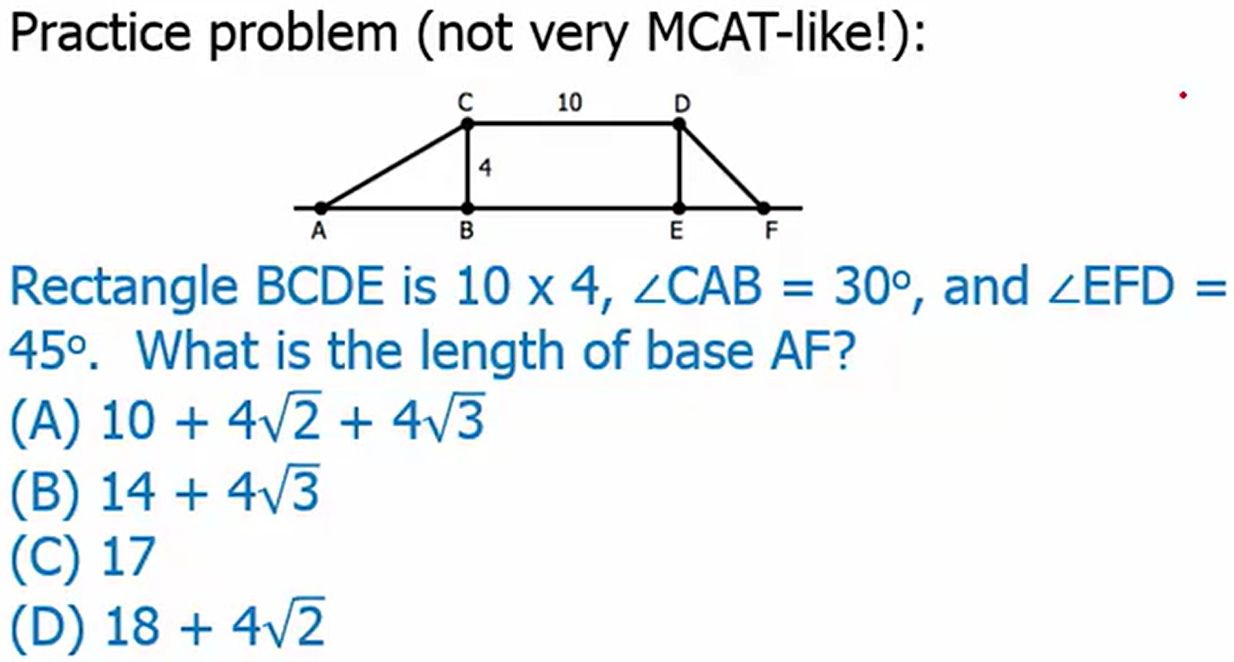
B. 14 + 4(sqrt(3))

Ratio of AB to BC is sqrt(3) : 1, so we must multiple by 4 to get BC = 4 so AB = 4 x sqrt(3)

N = b^k solve for b and k

log_b(N) = k

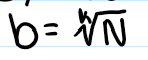
Limit the Bases

1. Common logs (base 10): written log (N), that is, w/o any explicit base

2. Natural logs (base e): written ln(N)

The number e (Euler’s constant)

e = ~2.718

Common Logs

log(10) = 1

log(100,000) = 5

log(1/100) = log(10^-2) = -2

N = 10^k → log(10^k) = k

substitute

log(N) = k → N = 10^log(N)

If log(N) goes up by 1, this means N gets…

If log(N) goes up by 3, N gets…

If log(N) goes down by 1, N gets…

If log(N) goes down by 5, N gets…

10x bigger

1000x bigger

Divided by 10

Divided by 100,000

sqrt(10) = 10^1/2 → sqrt(10) = ~3

If log(N) increases by 1/2, then N is multiplied by ~3

If log(N) decreases by 1/2, then N is divided by ~3

B. 100,000

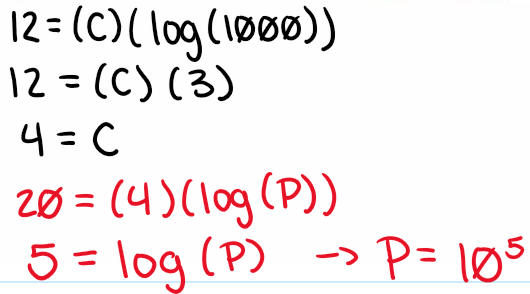
pH = -log[H⁺]

When pH goes down, the concentration of H⁺ ions goes up

pH < 7 = acidic and high # of H⁺ ions

pH > 7 = basic and small # of H⁺ ions

Sound Intensity and Decibels

B = 10 log(I / I₀)

I = the intensity of the sound wave itself

I₀ = the reference intensity, typically, the minimal threshold of human hearing

B = the decibel value, which approximates how loud the sound seems to human perception

For every additional factor of 10 bu which I is multiplied, we add 1 to the logarithm…

The 1 is then multiplied by 10, so multiplying I by 10^N adds 10N to B (to the decibel)

Example:

Decibels increase by 25 = 2.5 has been added to the logarithm itself

Adding 2 means I is multiplied by 10² = 100 and adding 0.5 means I is multiplied by sqrt(10) = ~3

So I is multiplied by 300

B. 5.6

Increasing [H⁺] makes urine more acidic = lower pH

C. 250,000

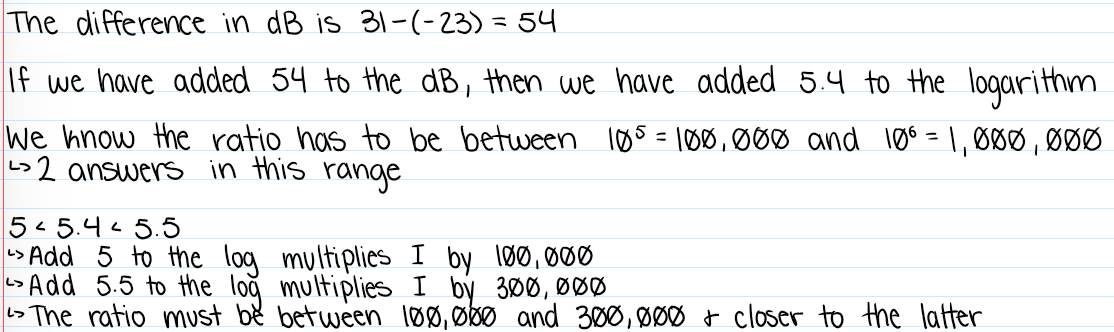
Rules of Significant Figures

1. All non-zero digits shown are significant

2. All zeros between non-zero digits are automatically significant

3. Ordinarily, all place-holding zeros would NOT be significant

4. Zeros tot he right of both the decimal point and all non-zero digits have no place-holding role and would be shown only if they were significant

5. A line over a zero makes it a significant digit (or write the decimal)

Arithmetic with Significant Figures

1. Addition/Subtraction Rule

   1. Place value: whichever term is measured to the least precise place limits the whole calculation

2. Multiplication/Division Rule

   1. Number of digits: whichever factor has the fewest digits limits the digits in the result

B. 9.0 × 10²³ atoms

Basic Laws of Exponents:

Treat the number in front and the powers of tens separately

C. 5.7 × 10²⁷ W

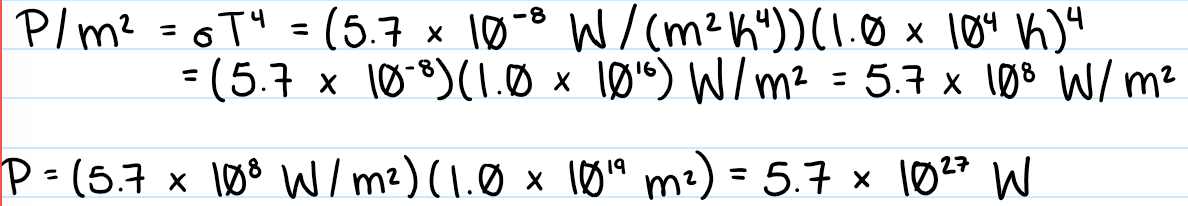
The most fundamental equation of motion is:

Distance = speed x time → x=vt

x_T = x₁ + x₂

t_T = t₁ + t₂

Can add individual distances or time, but can’t combine the individual speed to get a speed for the whole trip

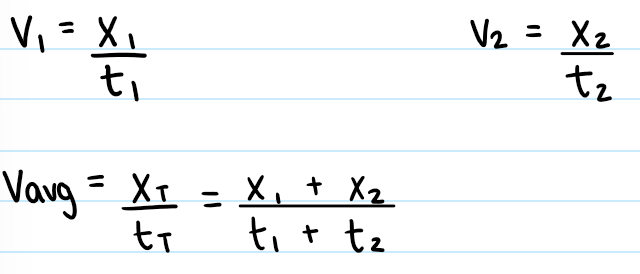
A. 30 mph

The fundamental equation for acceleration is:

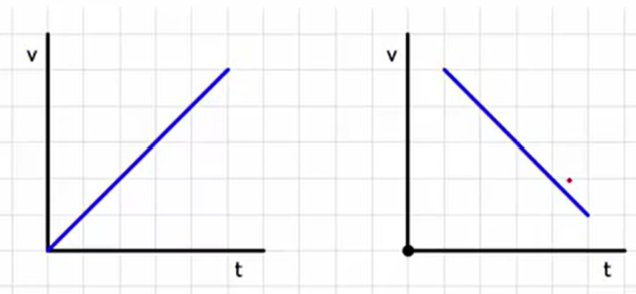
Uniform acceleration appears as a straight line on a v-vs-t graph

The slope on this graph equals the acceleration

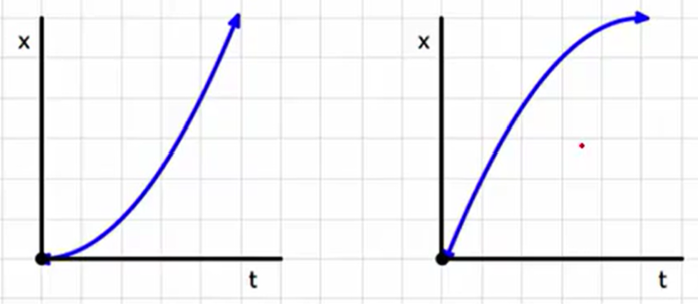
Uniform acceleration appears as a parabola on a x-vs-t graph

Slope = v

Right: v is increasing

Left: v is decreasing

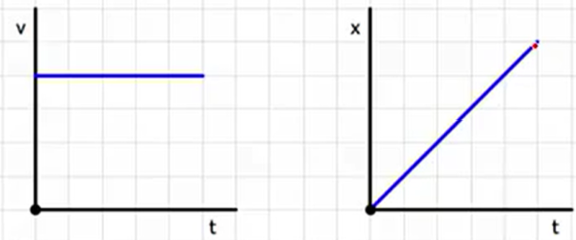
Constant speed appears as a straight line on x-vs-t graph and horizontal line on v-vs-t graph

Average Velocity Equation

Another equation: v_f - v_i = at

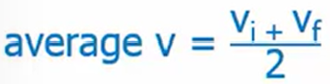
Time-Independent Equation

2ax_T = v_f² - v_i²

Another Equation:

x_T = ½ at² + v_it

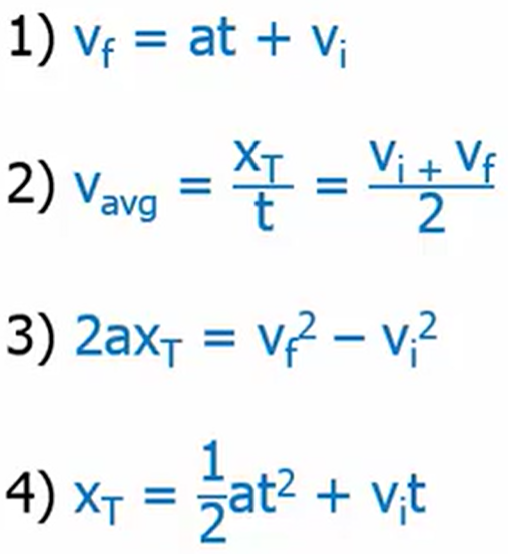
B. 50 m

Gravitational Field

g = 9.8 m/s² = ~10 m/s²

Freefall acceleration doesn’t depend on mass

1. For very light objects air friction is significant, so their motion cannot be considered true freefall

2. Over a large enough drop, any object will get fast enough to reach terminal velocity

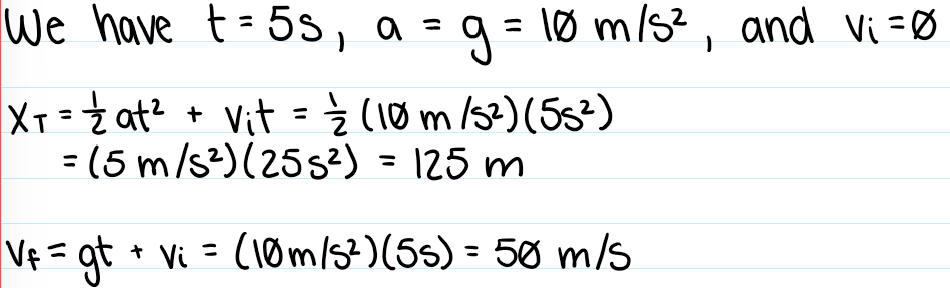
A. 200m, 70 m/s

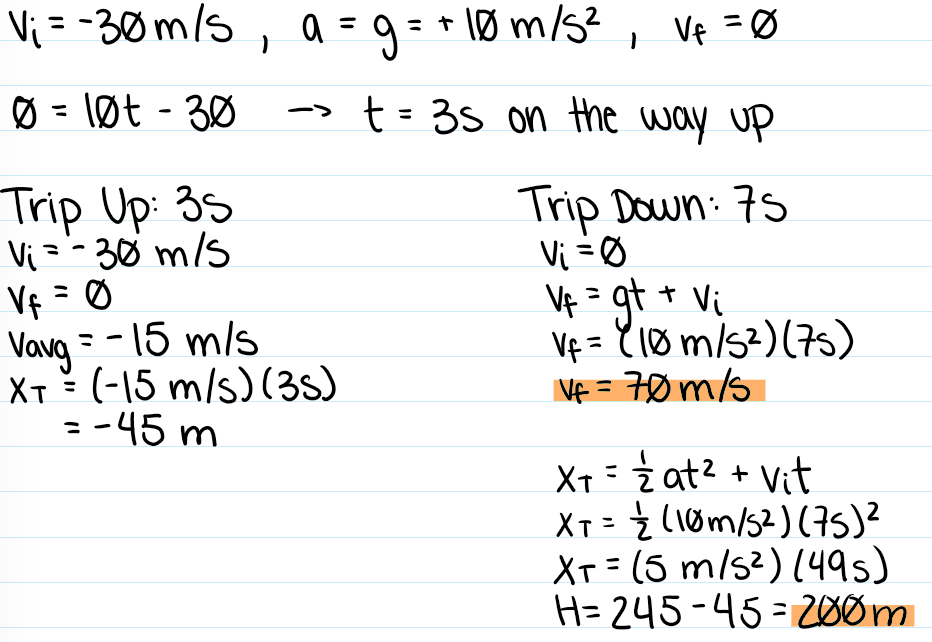
Scalars

Physical quantities for which direction is not meaningful

Vectors

Physical quantities that inherently have a direction

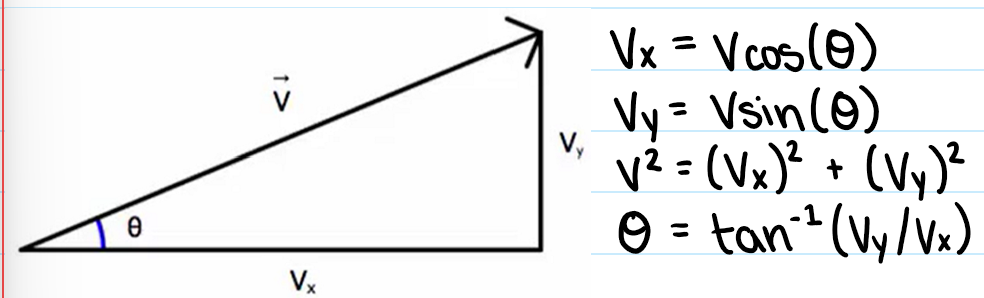
Vector Addition

Put arrows tip to tail

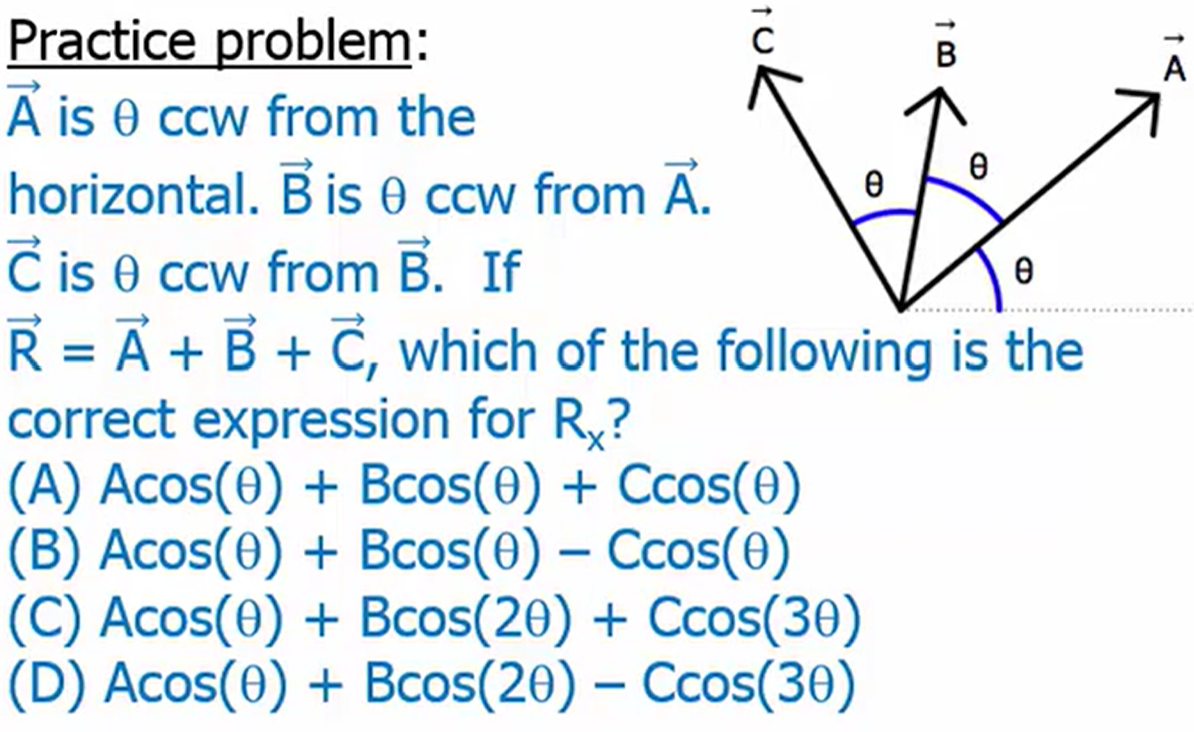
C. Acos(theta) + Bcos(2 theta) + Ccos(3 theta)

Distance vs Displacement

Distance: the total amount walked/driven on the ground

Displacement: the relationship of ending point to starting point

Speed, Velocity, and Acceleration Relationship

If you change speed, you change velocity

Can change velocity while maintaining a constant speed

Acceleration: time rate of change of velocity, not speed

• a_c = v²/r

What are Dynamics?

Why things move

1 N = 1 (kg x m) / s²

Unit force is a newton

Newton’s First Law

“Law of Inertia”

An object at rest stays at rest, and an object in motion at a constant velocity stays in motion, unless acted upon by an unbalanced force

Inertia

The tendency of mass to resist changes in its state of motion

Balanced vs Unbalanced Forces

Balanced: No change in motion

Unbalanced: Change in motion

Newton’s Second Law

F = ma

F = vector sum of the forces on the object (the “net” force)

m = mass

a = acceleration

Newton’s Third Law

“The Law of Action and Reaction”

For every action, there is always an equal and opposite reaction

Applies to mechanical contact, gravitational, and electromagnetic forces

Weight

The force of attraction that Earth’s gravity exerts on this mass

Depends on mass and gravitational field: Weight (w) = Mass (m) x Gravity (g)

Normal Force

The weight of the object makes it press into the surface on which it is sitting causes the surface to push back on the object

N = w = mg

What if the surface is slanted?

If the horizontal surface is accelerating upward, then the net force has to be upward, so the normal force is slightly larger than the weight

If the horizontal surface is accelerating downward, then the net force has to be downward, so the normal force is slightly smaller than the weight

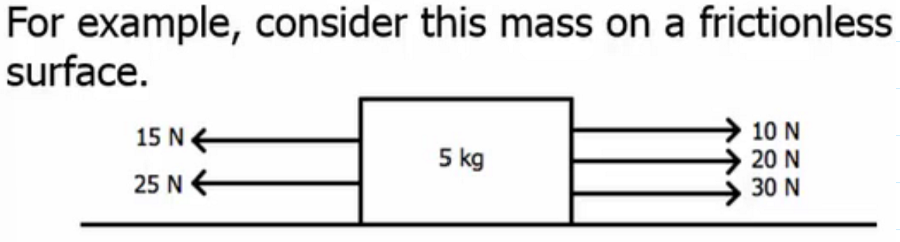
If forces are at angles:

Find or estimate components

If an object is at rest or constant velocity: the components in both x- and y-directions should sum to zero

If any acceleration is in one direction (x or y), then the components in the other direction will sum to zero

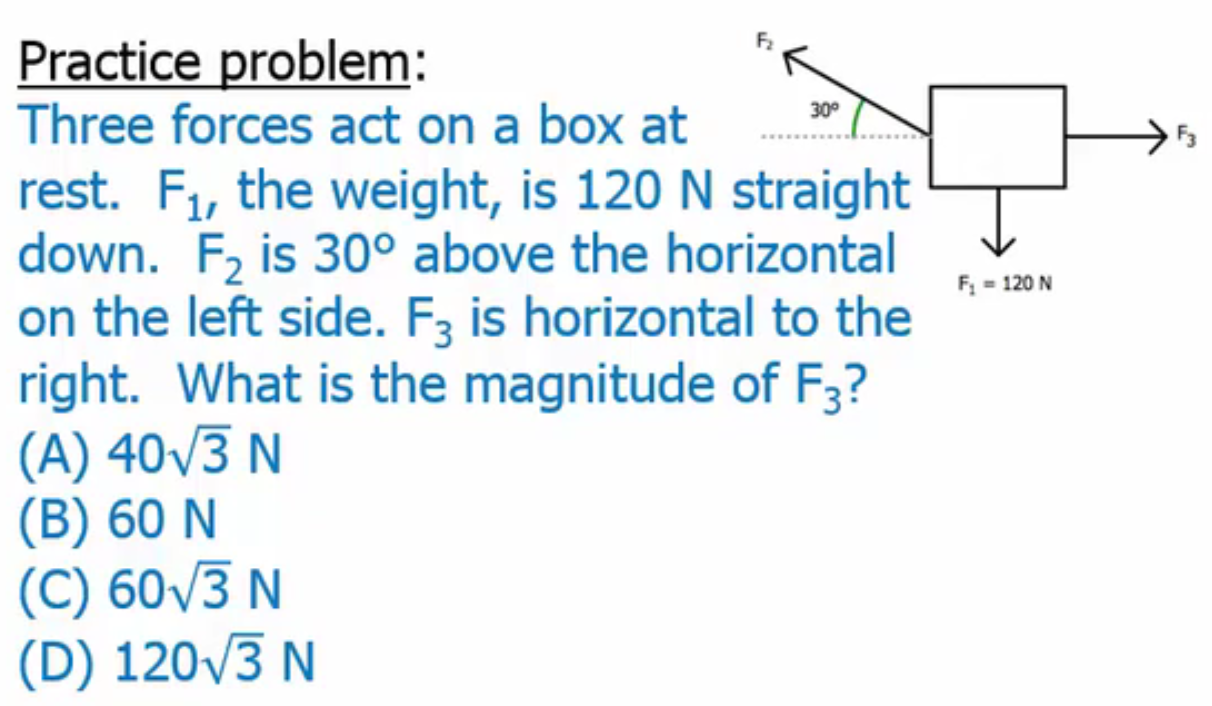
D) 120sqrt(3) N

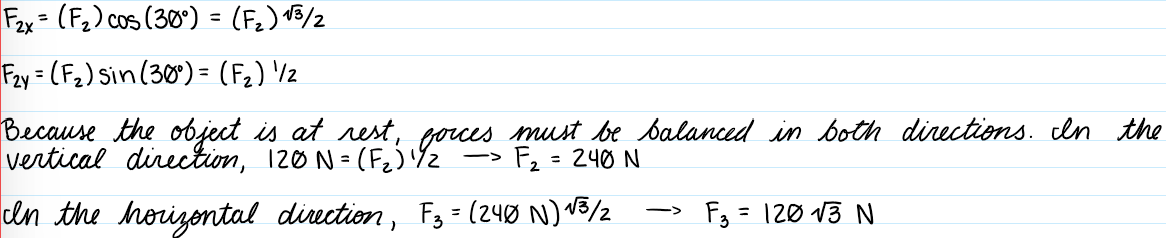
Friction

A force that opposes motion

Arises from two surfaces rubbing together

f = uN

f = force of friction

N = normal force

u = coefficient of friction (between 0 and 1)

• Close to zero for slippery surfaces

• Larger for rough or sticky surfaces

Static Friction

The friction locking an object at rest

Need to be broken to initiate motion

u_s > u_k

Kinetic Friction

The friction that happens once something is already sliding, in motion

u_s > u_k

B) 5 m/s²

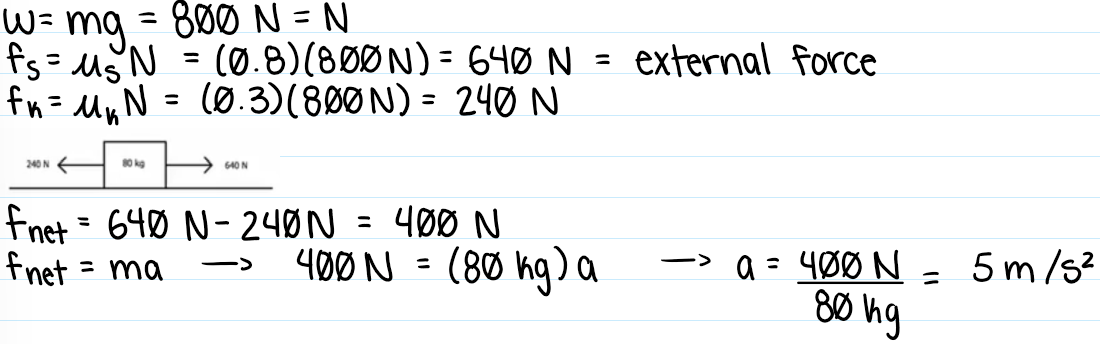
Free Body Diagrams

Represents the mass, the object, as a point

Represents all forces as arrows

A) 1.25 m/s²

How to solve for inclines

Divide weight into two components

• One perpendicular to the slope (w_perp)

• One parallel to the slope (w_par)

Low values of Theta, w_perp would be bigger and w_par small

Values of Theta close to vertical, w_par would be large and w_perp small

Can find w_perp and w_par using SOHCAHTOA

w_perp = w(cos(theta)) = mg(cos(theta))

w_par = w(sin(theta)) = mg(sin(theta))

Perpendicular Direction:

No motion at all

Forces are balanced

N = w_perp = mg x cos(theta)

Friction Force in terms of w_perp

N = w_perp = mg x cos(theta)

f = uN = umg x cos(theta)

Equations connecting w_perp and w_par

N = w_perp = mg x cos(theta)

f = uN = umg x cos(theta)

F_net = w_par - f

F_net = mg x sin(theta) = umg x cos(theta)

F_net = mg(sin(theta) - ucos(theta)) = ma → cancel out the m’s

g(sin(theta) - ucos(theta)) = a

Suppose the mass doesn’t slide:

If u₂ is greater than or equal to tan(theta), the mass can sit on the incline

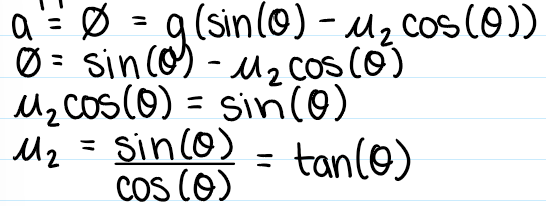
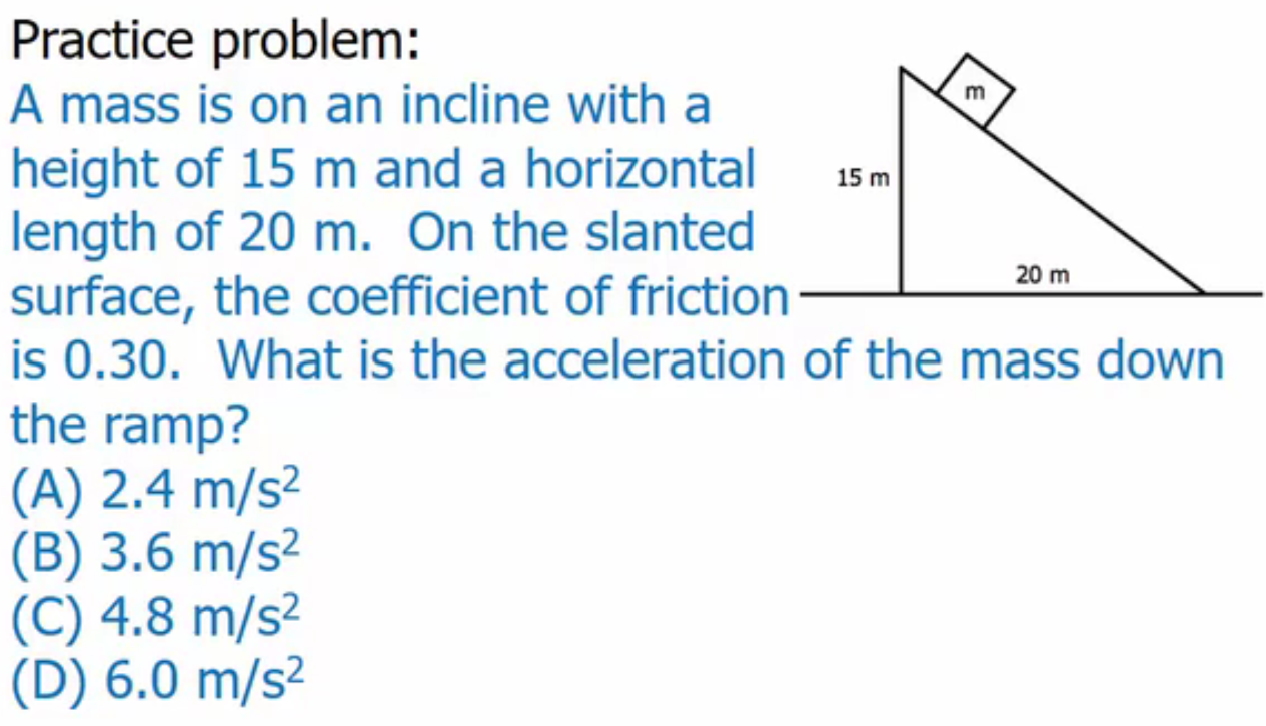
B) 3.6 m/s²

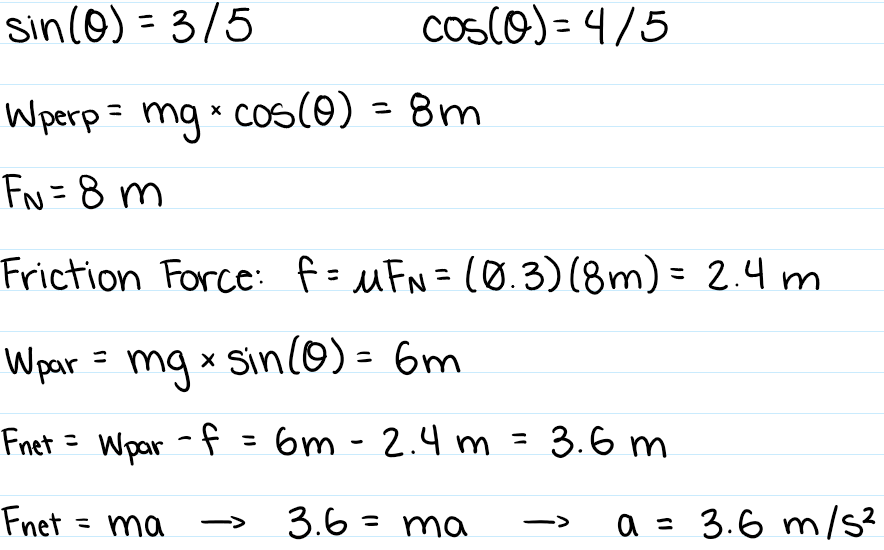
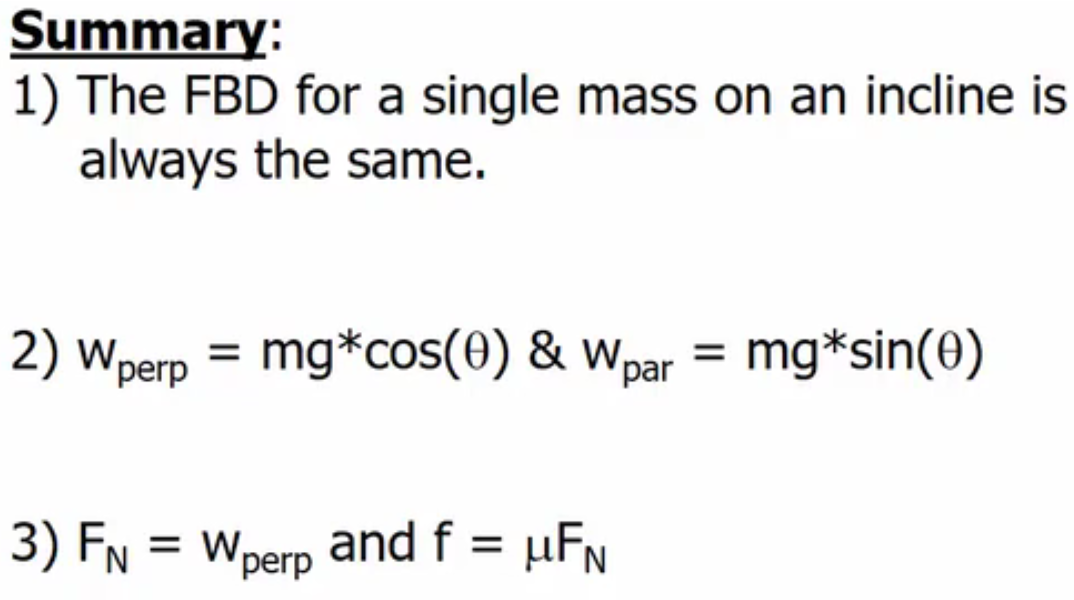
Balanced forces (N1) are two or more forces on the same object →

Equal & opposite forces on the same object always cancel

Action and reaction (N3) are always on two different objects →

They are always equal & opposite, but never cancel

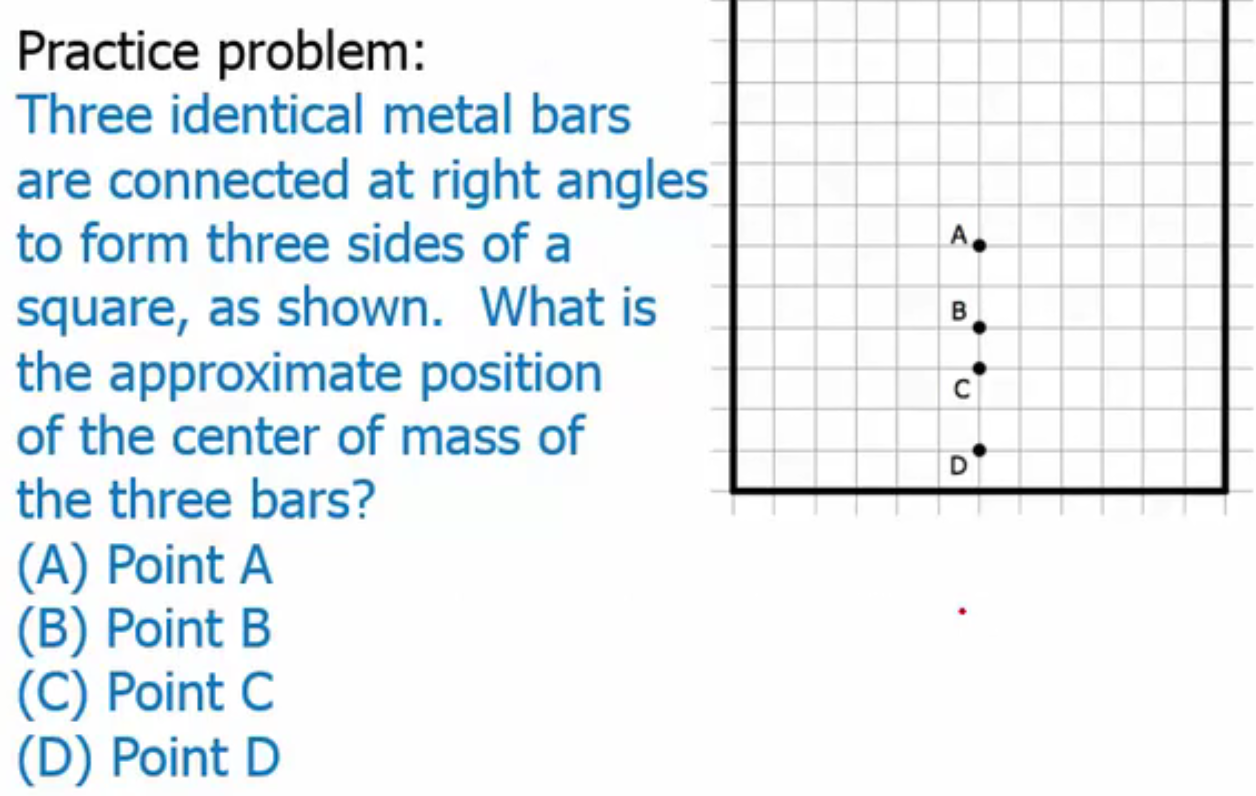
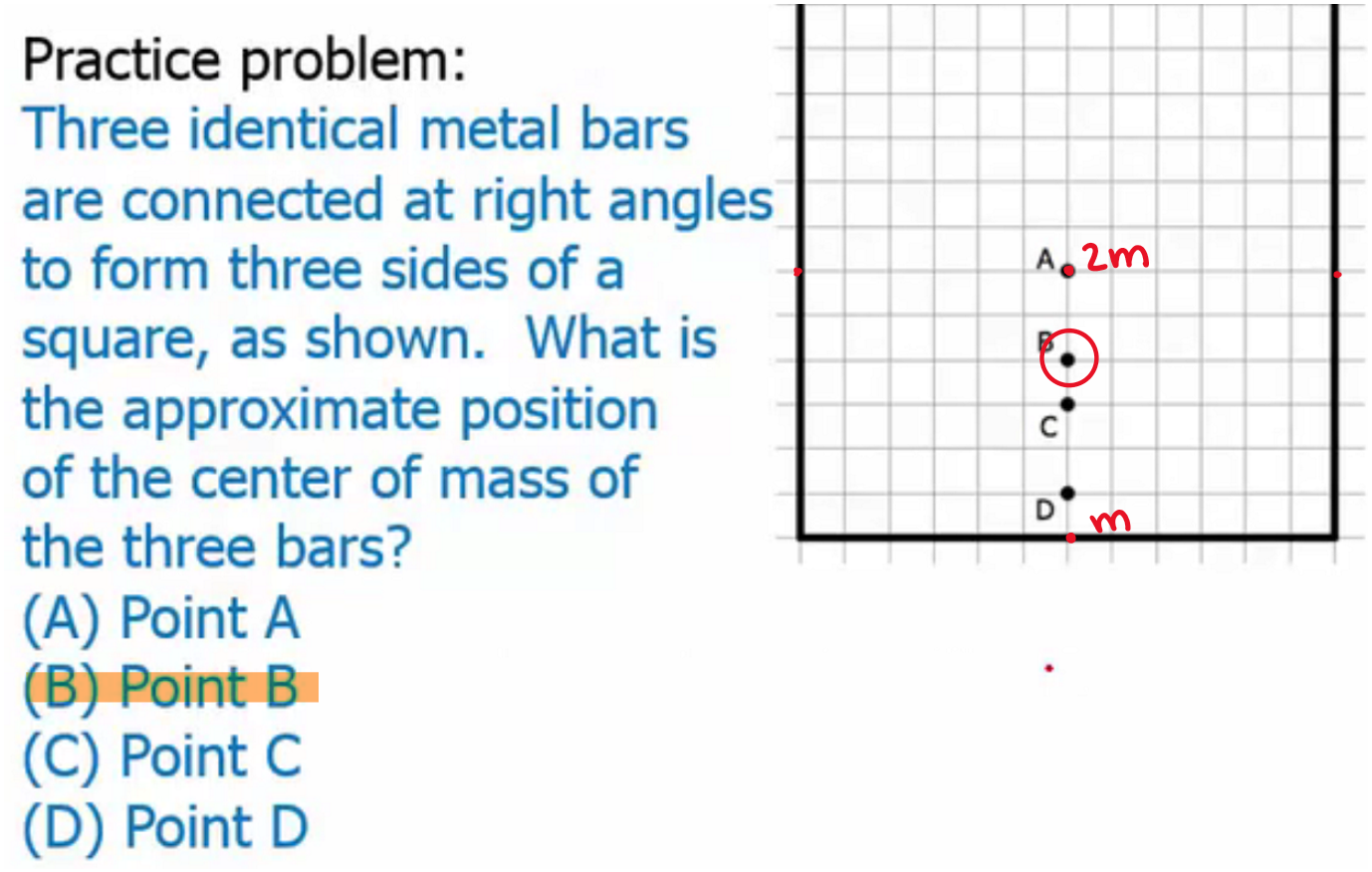
Center of Mass Definition

All the mass of an object is concentrated at a single point

Changes as the body assumes different positions

Center of Mass Formula

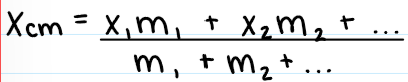
If masses were spread over a 2D array, w/ x- and y-components:

x_cm = sum of (m_i)(x_i) divided by total mass

y_cm = sum of (m_i)(y_i) divided by total mass

A force applied at the center of mass of an object will accelerate the object

A force applied offline from the center of mass can also twist or spin the object in addition to moving it

Torque (T)

A way to express the “leverage” that a force has because it acts at some radius from its target

T = Fr x sin(theta)

F = the force, which as a vector naturally has a direction

r = the displacement vector from the center of rotation tot he point where the force is applied (“distance”

theta: the angle between F and r

When theta = 90 degrees

F and r produce the maximum possible torque

When theta = 0 degrees or 180 degrees

sin(theta) = 0, so there is no torque at all because the force is exactly in line with the center

When torques are balanced:

T_ccw = T_cw

C) 1500 N

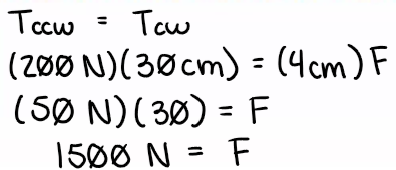
Statics:

The student of the forces in play when things are sitting still

For any physical object that is still, it must be true that:

• All forces are balance (in all directions)

• All torques are balanced

The two requirements result in two different equations for two unknowns

D) T₁ = 1625 N, T₂ = 375 N

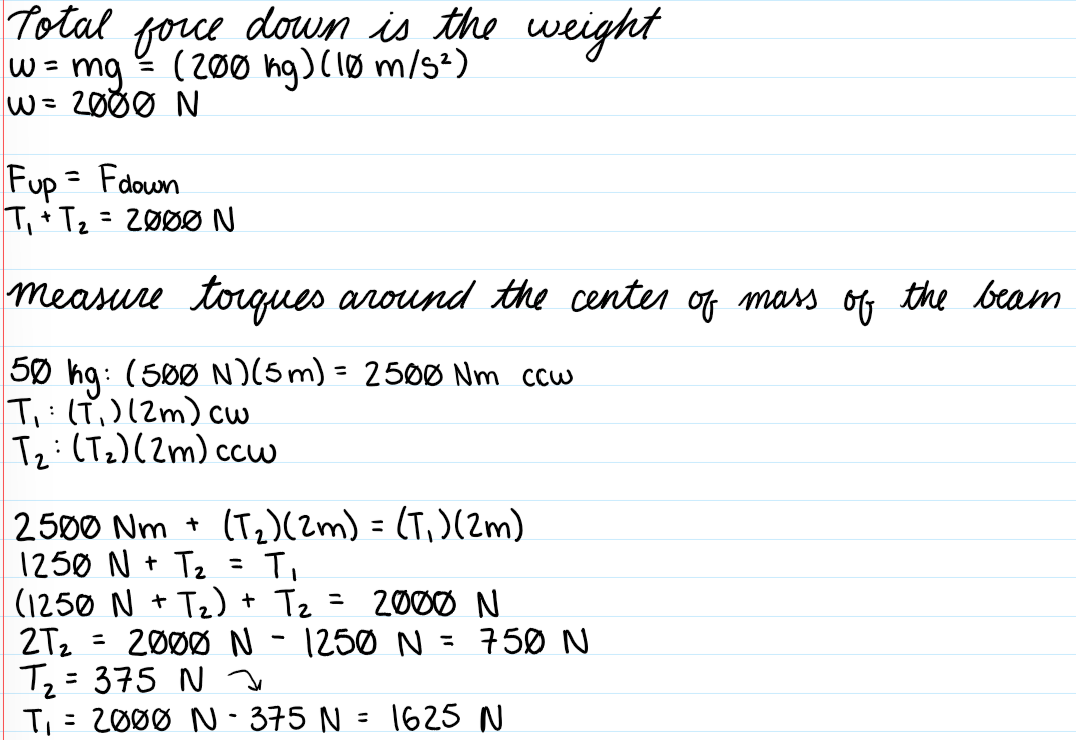
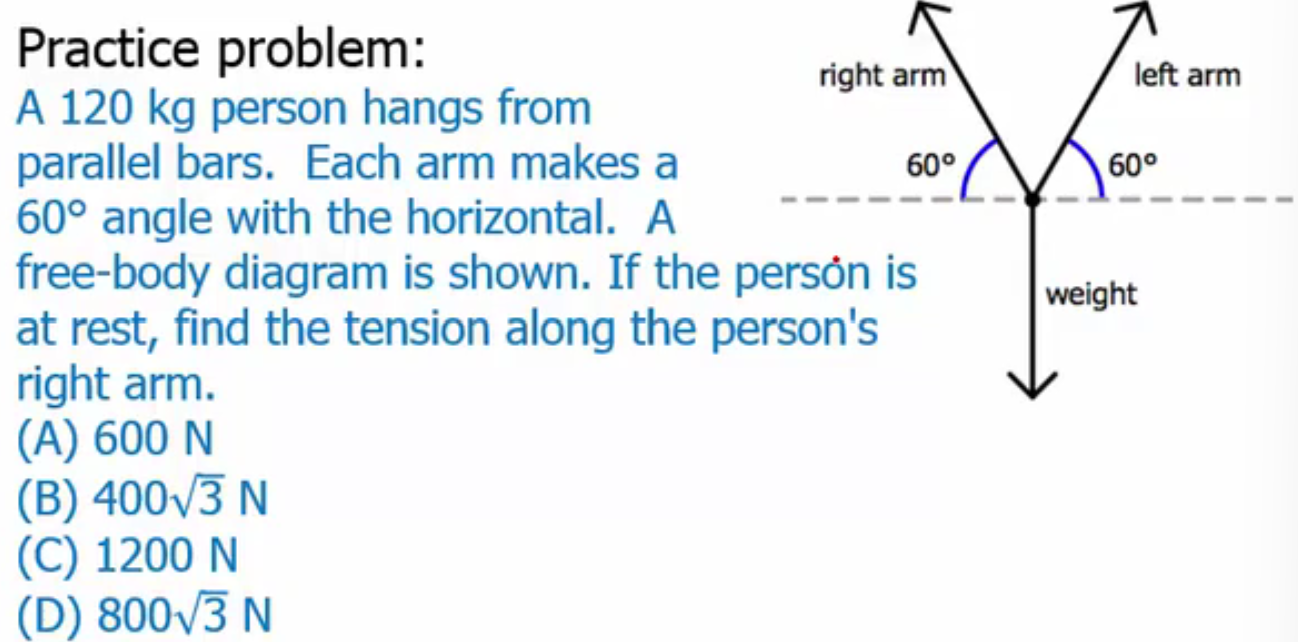
B) 400sqrt(3) N

Bilateral symmetry:

• two x-components of the forces are equal and opposite, so they cancel out

• two y-components of the forces from the arrows are equal and combine to an upward force that balances the weight

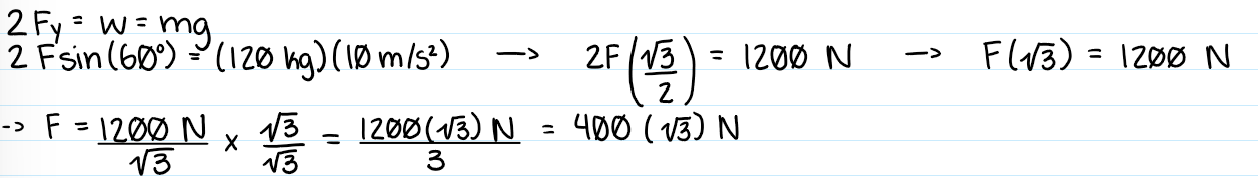
Energy Definition

The ability to do work

Lifting, moving objects, or changing their velocity

Units of Energy

Joules = N x m

Gravitational Potential Energy

GPE = U_g = m x g x h

Linear relationship with mass or height and energy

Depends on an object’s mass, gravity’s acceleration, and height

The lowest point in a problem has zero gravitational energy

Spring Potential Energy

SPE = U_s = ½ k _* x²

k = spring constant

• Higher = less stretch

x = distance the spring is compressed or stretched

• Greater stretch = more energy stored

Kinetic Energy

KE = ½ m _* v²

An object’s energy increases with its mass and the square of its velocity

• The heavier and faster the object = greater KE

A. A 75 kg person hikes a vertical distance of 100 m