Lecture 4: Passive Properties and Excitability

Equivalent Circut Model

• A theoretical circuit that retains the properties of whatever is being modelled in its simplest electrical form

Equivalent Cell Model of Cell Membrane

• Representation of the specific ion channels and their associated E_ions (the battery symbols) and conductance (the variable conductance symbols) in series as well as the membrane’s capacitive properties (the capacitance symbol)

  • Battery: electrochemical gradients for ion channels

  • Conductance: ion channels

  • Capacitors: cell membrane physical properties

• Used to predict a neurons excitability use this as a modelling construct to predict membrane behaviour and how processes contribute to its excitatory activity

Batteries

• Devices that generate a voltage known as the electromotive force (emf)

  • in series with conductance in a circuit

What is an electrochemical ion gradient?

• a source of electrical energy, similar to a battery.

Electromotive Force (emf)

• Energy per unit charge that is supplied by a source of electrical energy

• E_ion: the equilibrium potential for ions associated with a particular set of ion channels (a source of electrical energy)

  • Measured relative to 0 to identify driving forces causing current flow

• It is the equilibrium potential (Eion) for these ions of a given channel

  • emf_ion = E_ion

Voltage/Driving Force

• The difference between the measured transmembrane voltage V_m and calculated value of E_ion:

  • V_m - E_ion

• Units: Volt (V)

Conductance

• A measure of how readily a current will pass through a material (G).

• Inverse of resistance (R), a measure of how much the material opposes the flow of current

• Ion Channel: represents ion channel permeability

• Assigned Units: Siemens (S) or ohm^-1 (Ω^-1)        

• Represented as a variable rather than a constant

Importnace of Conductance

• Determines the size of the current that will flow across the membrane associated with a particular set of ion channels

  • Determined by the membrane potential relative to the equilibrium or reversal potential for that current

• Determines the size of I_ion at a particular V_m relative to E_ion, and is determined by Ohm’s law:

  • (V_m – E_ion) = I_ion/G_ion      

• Must take driving force into account so that there is ZERO current flow when V_m = E_ion.

  • Everything must be measured relative to that position

Capacitor

• Devices that store charge

• Consist of two conductors separated by a non-conductive material - dielectric/insulator

  • The more voltage applied the more charge that is associated, as the charge on either side of the dielectric and can sense what is happening on the other side and becomes charged as a result

Components of a cell membrane that allow it to act as a capacitor”

• The cell membrane is composed of phospholipids, a non-conductive dielectric material.

• The intracellular and extracellular fluids are highly conductive due to the presence of ions.

• When a voltage is applied across the membrane, charge accumulates on either side, making the membrane act like a capacitor.

Capacitance Law

• Defines the amount of charge associated with a system:

  • Capacitance (C) = stored charge (Q)                                           

    voltage (V)      

  • Q is measured in Coulombs (C)

  • Units: Farad (F)

• Impacts the waveform generated in an excitable system

Cell With A Non-Conductive Membrane

• As membrane potential changes, the amount of charge stored on the membrane fluctuates, appropriately

Cell With A Conductive Membrane

• The potential difference changes causing the charged stored must change

  • if potential difference ↑ (more hyperpolarised), then stored charge ↑

      more charge associated

  • if potential difference ↓, then stored charge ↓

      relationship between charge and voltage 

• i.e bigger potential difference – more charge associated with the membrane, and vise versa

Capacitive Currents (I_c)

• Current present in the system to accommodate charge

  • Moves on and off the capactior

• Flow whenever the membrane potentail

What happens to current when there are changes in membrane voltage?

• Some of the current will become stored charge associated with the membrane.

• Or, if charge has moved off the membrane, it will appear as current.

Interaction Between Ion Movement and Membrane Capacitance

• Even with ion movement, minimal changes in ion concentrations occur during typical membrane potential changes.

• This is because only a small number of ions are needed to accommodate the capacitance property of the membrane.

Factors Determining Membrane Capacitance

• Determined by the phospholipid content and surface area of the cell membrane.

  • Cell membrane phospholipid content is a relatively constant construct = constant capacitance per unit area

  • Surface area of cell membrane determines total capacitance – impacts cell’s electrical properties

    • Cell with large surface area – large amount of capacitance

• Membrane capacitance can be used to measure cell surface area/siz

Specific Membrane Capacitance

• A biological constant

  • 1μFcm^-2 (μF/cm²)

Simplification of Equivalent Circuit Model

• Possible when below firing threshold, as RMP is stable

  • No voltage-gated changes in conductance seen (to generate action potentials)

Key Features of Equivalent Circuit Model

• Cell membrane behaves as a capacitor and conductor in parallel

• The equilibrium potential is determined by the electrochemical gradient associated with the conductance – describes the electrochemical behaviour of the cell membrane

Total Conductance at Rest

• Sum of all conductance

Current Associated With The System

• The sum of all currents flowing through the system

  • Allows us to define the equilibrium position for the system

How Can RMP Be Predicted From Equivalent Circuit Model

• Take the current equation and swap in the equivalence of the current for equilibrium positions and associated conductance – isolation of equation to calculate the final equilibrium position

  • can then predict ______

Simplified Equivalent Circuit Model: At Rest

• No current flow because they reach the equilibrium position where the ionic gradients have a set position where the membrane potential + the equilibrium position of ions associated with the active conductance

• RMP derived from the relative contribution of conductance and the total conductance and equilibrium position of key ions

   

Passive Response of A Neuron

• A change in the membrane potential of a neuron in response to a current injection.

  • Doesn’t generate an action potential

• Current injected - a square step current

• The voltage response does not instantaneously follow the current response due to the electrical properties of the membrane.

• Negative current injection causes hyperpolarization.

• Positive current injection causes depolarization.

Square Step Current

• A current that has a constant amplitude for a certain period then gives rise to instantaneous/abrupt changes in current → different constant amplitude.

  • Can be used to monitor voltage response and characterise cells from recordings

Injection of Negative Currents:

• Hyperpolarization

  • ↑ intracellular negativity

Injection of Postive Current

• Depolarization

  • ↑ intracellular positivity

What Must Be Adressed For A Current to Flow Across The Memrbane

• Presence of conductance and capacitor

  • During response, V_m no longer = RMP

  • Voltage response doesn’t reflect the time course for which voltage changes occur

Injection of Square Step Current: Voltage Response

• Slowly evolving phase: voltage starts to change

• Eventually reaches a steady state and achieves a voltage level from the current level predictable by Ohms law

  • Change is only seen in neurons after a period of time

Square Step Current-Voltage Response: Conductance Only Circuit

• If a cell was a conductance-only system, with no capacitance, it would respond instantaneously

• A square-step of voltage – not due to the capacitance associated membrane but the current changing with the capacitor

• The current must flow onto/ off the capacitor to obey capacitance law – occurs when positive charge is injected = slowly evolving voltage response

Square Step Current-Voltage Response: Conductance + Capacticance Circuit

• The amount of current flowing onto the capacitor over time and the amount of current flowing through the conductance over time – adds up to the total current injected  

  • Some current is used for different tasks until an equilibrium is reached (charge is taken and used to ensure capacitance law is obeyed) – all current injected is sustained through conductance and a stable membrane potential is achieved

  • When MP is stable – no charge is required to be associated with the capacitor

    • Capacitance current is ~0

Time constant (t)

• The time it takes for the voltage across the capacitor to decay to 63% of its initial value (and reach a steady state

  • (ΔV_m) = 63% 

• It is calculated as the product of the resistance and capacitance of the circuit.

• A larger time constant means that the voltage decays more slowly.

• Determined by

  • Directly proportional to capcitance

  • Inversely proportional to conductance

Calculation of Voltage

•        V = Q

             C  

• Capacitance = charge stored on capacitor/ voltage  

• Rearranged to find voltage: Charge in capacitor/ capacitance

Differentiation and Rearrangement of Capactiance Equation

• The rate of change of voltage is equivalent to the rate of change of charge flow divided by capacitance

  • Differentiated using time derivative

• Rate of membrane potential change for any given current i.e the same current is inversely proportional to membrane capacitance

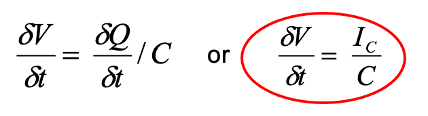
Current

• Rate of change of charge flow

  • I.e. current associated with the membrane determines how quickly voltage is changed and is inversely related to capacitance

Relationship Between Membrane Capacitance And Changes in Membrane

• The rate of change of membrane potential is inversely proportional to membrane capacitance.

• This means that a larger membrane capacitance leads to a slower rate of change in membrane potential for a given current.

Affect of Size On Capacitance

• Size determines capacitance, capacitance determines the rate at which a voltage can change in a biological system with electrical properties

Total Membrane Capacitance: Large Cell

• Slower voltage response(red)

• Higher capacitance

  • Takes longer to reach a voltage steady state

Total Membrane Capacitance: Small Cell

• Faster voltage response (blue)

  • lower capacitance

Affect Of Capactior on The Rate of Voltage Change in a Circuit

• Capacitor slows down the rate of voltage change in a circuit.

  • in parallel to the resistor. inverse of conductance

• The larger the capacitance, the slower the rate of change.

• This is because a capacitor stores charge, which takes time to build up or dissipate.

• The time constant of a circuit, which is the product of the resistance and capacitance, determines how quickly the voltage change

How Can The Rate of Decay of Voltage Change In Response to A Capacitor Be Defined?

• Define as an exponential function:

  • Current-voltage = starting voltage x e^(-t_/RC)

  • Can estimate the time at which the voltage has changed by 63% (0.37 of OG value) the time given by the equation = resistance x capacitance

Relationship Between TIme Constance And Capacitance (C)

• Directly proportional e.g.

  • ↑ ________ → ↑ time constant (t) and vice versa

  • Longer to reach steady state – direct relationship

Relationship Between Time Constant and Conductance (G):

• Inversely proportional

  • e.g. ↓ _______→ ↑ time constant (t) and vice versa

  • Large time constants\; low _____

Importance of Time Constance

• Determine the amount of lag of voltage response following the membrane current as a result of membrane capacitance

  • The larger the constant the greater the lag.

Use of Positive Current Steps

• Manipulate the membrane potential towards firing threshold and depending on i ts size, generate multiple acitpion potenitals

Effect of Capacitance on Excitability

• Usually constant as cell surface area does not change

  • Unlikely without drastic manipulation

• Determines the frequency of the response

  • Larger capacitance leads to a slower response time - difficult for them to reach threshold and fire an action potential.

  • This means that brief, high-amplitude stimuli are more effective at triggering action potentials in neurons with high capacitance.

• Increasing CURRENT = MORE RESPONSIVE SYSTEM

Effect of Conductance of Excitability

• Does change and has 2 effects

  • Determine the steady-state voltage  

  • Affects the time constant – opposing effects

Voltage Response in Response to Decreased Conductance

• Modification of conductance impacts when the voltage response is likely to reach the threshold

  • Increase of system conductance – (ohms law) – voltage level achieved would be lower 

  • Increasing conductance reduces the excitability of the system

  • Subthreshold response with decreased conductance would be more likely to reach a threshold  

Ohms Law

• Determines the steady state voltage response amplitude to the same current stimulus

  • V = I/G [Ohm’s law]

• Inversely related is the ability of a neuron to fire

  • When membrane potential (MP) reaches threshold, conductance increases, leading to higher excitability.

  • Decreased conductance → system more likely to fire at the steady state.

Neuromodulation

• Modifies resting membrane conductance to cause the opening or closing K⁺ channels that contribute to conductance

  • e.g. ACh, GABA, glutamate, noradrenaline serotonin

Affect of Conductance on the Time Constant

• t = C/G

• Affects the time point at which firing can occur – modifies the time constant

• Increased conductance, reduces membrane excitability at the steady state, but changes (↓) the time constant to allow the threshold to be reached earlier (vice versa)

What Does Fast Neuron Transmission Rely On

• Rapid conductance changes

• Speedd up the responsive of the membranes ion channels implicated