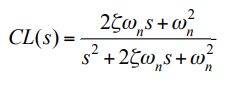Control Systems - My Latest Edit

Plant

Component/Factor you want to control

Sensor

Detects change in factor

Controller

Adjusts the signal to the plant

Setpoint

Desired value, compared to measured value

Hysteresis

The difference between the measured value and the setpoint value.

{Essentially shows that the actual change lags behind the desired ideal change}

Laplace operator

s = jω

Operations in the s domain

Change in Time domain ≡ Equivalent change s domain

Integrating by dt ≡ multiplying by 1/s

Differentiating by dt ≡ multiplying by s

Single-Loop feedback system

Fraction of output signal (V_o) is measured and subtracted from the input signal (V_i) to create an error signal (V_e).

V_e = V_i - kV_o → where k is a fraction {determined by the components on the feedback loop}

Open Loop transfer function (OLTF)

No feedback loop connection

OLTF = Forward loop combination

OLTF = G(s)*H(s)

Closed-Loop transfer Function (CLTF)

V_o / V_i = G(s) / (1 + G(s)*H(s))

• G(s) is the transformation on the forward loop

• H(s) is the transformation on the feedback loop

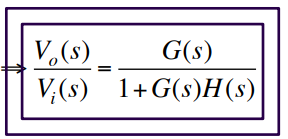
Determining theType of a control system

Determined by the number of poles at the origin in the s domain, in an open-loop transfer function (OLTF)

• Also seen as the number of integrators in feedback the system

• {Essentially where the denominator of an open-loop trasnfer funtion of a control system = 0, and the number of times where s = 0}

Example:

G(s)H(s) = 1/s(s+1)(s+2) → Type 1

ALWAYS USE OLTF TO DETERMINE TYPE

MUST ALSO BE IN A NEGATIVE UNITY FEEDBACK {H(s) = 1}

Determining the Order of a Control system

The greatest order of power of s in a closed-loop transfer function (CLTF).

{Also can be stated as the total number of poles of a system}

Example:

CL(s) = G(s)/ (1+G(s)H(s)) = 2s/(s²+2s+1)
→ Order of this system is 2 as largest power of s in the denominator is 2.

CLTF [1+G(s)H(s)] or OLTF [G(s)H(s)] can be used

Type Zero Control System

• Proportional loop (K_p)

• No integrators in control loop

• Finite steady-state error (SSE) to a step input

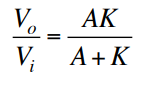
Type I control system

• Integral loop

• One integrator in control loop

• Zero steady-state error (SSE) to step input

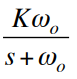
Type II control system

• Integral Loop

• Two integrators in control loop

• Zero steady-state error to ramp input

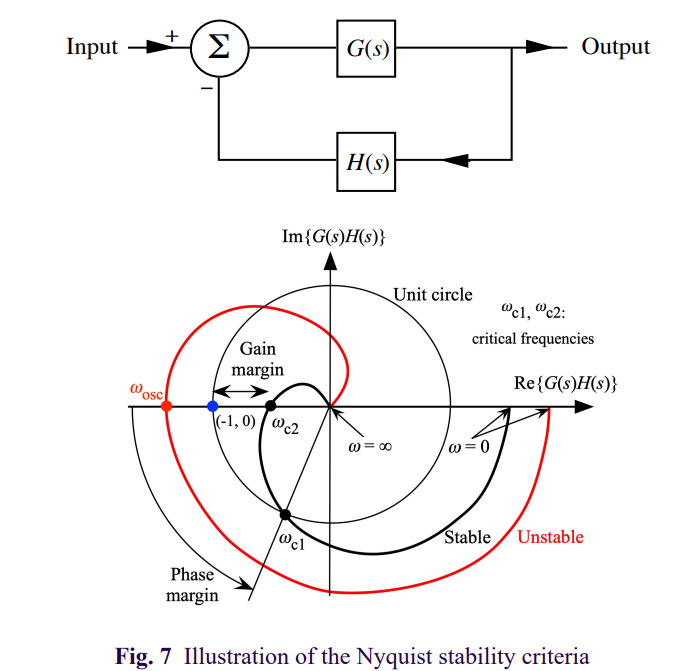
Stability of a control system that can vary with Frequency

• Gain margin → Difference in magnitudes of the OLTF of the control system and at unity.

• Phase margin → Phase difference of the control system at unity, measured from the negative Real axis on the argand diagram

Type of a system and its SSE to an input
(Notice the pattern regarding type, and finite/infinite SSEs)

Classic Second order type 2 system

CL(s) = (2ζω_ns +ω_n²) / (s² + 2ζω_n +ω_n²)

where ζ is the damping factor