Data Structures and Algorithm

Sorting Algorithms

• Bubble

• Selection

• Insertion

• Shell

• Heap

• Merge

• Quick

• Bucket

• Radix

Divide and Conquer Algorithms

• Merge

• Quick

Bubble Sort

• Simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order

• Right side sorting

Bubble Sort Complexity

• Best - O(n)

• Worst - O(n^2)

• Average - O(n^2)

Bubble Sort Algorithm

Use Cases

• Best - Ω

• Worst - O

• Average - Θ

Common Time Complexity Symbols

• O(1) - constant

• O(log n) - logarithmic time

• O(n) - linear time

• O(n log n) - log-linear time

• O(n^2) - quadratic time

• O(2^n) - exponential time

  O(n!) - factorial time

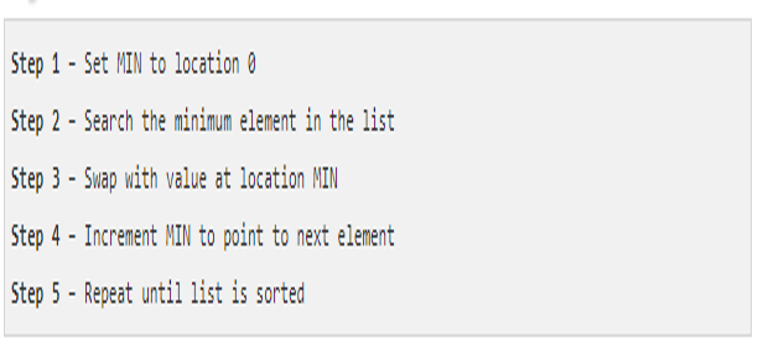
Selection Sort

• Repeatedly finding the minimum element considering ascending order) from the unsorted part and putting it at the beginning

• Left side sorting

Selection Sort Complexity

• Best - O(n^2)

• Worst - O(n^2)

• Average - O(n^2)

Selection Sort Algorithm

Insertion Sort

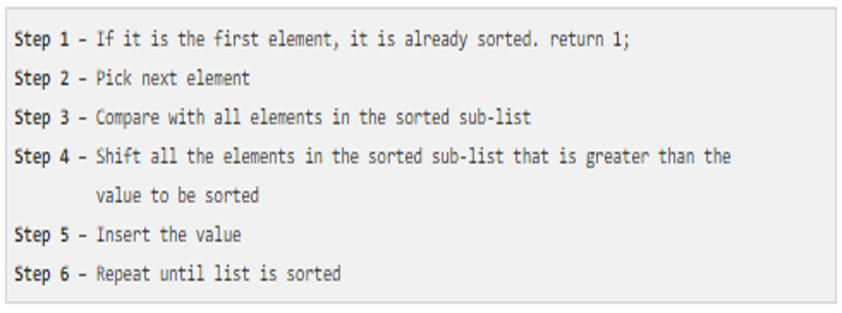
• In-place comparison-based sorting algorithm

• Left side sorting

• Bubble sort, but only for one element at a time

Insertion Sort Complexity

• Best - O(n)

• Worst - O(n^2)

• Average - O(n^2)

Insertion Sort Algorithm

Shell Sort

• Long-distance insertion sort

Shell Sort Complexity

• Best - O(n log n)

• Worst - O(n^2)

• Average - O(n^1.5)

Shell Sort Algorithm

1. Choose a gap sequence: Start with a large gap and progressively reduce it. A common sequence is n/2, n/4, ..., 1, where n is the size of the array

2. Perform Insertion Sort for each gap: For each gap, perform an Insertion Sort where elements that are gap positions apart are compared and swapped

3. Repeat until the gap becomes 1, and the array is sorted

Shell Sort Optimal Sequences for Gaps

• Original - n/4, n/4, ..., 1

• Knuth - (3^n - 1)/2

• Sedgewick -1, 5, 19, 41, 109, ... (formula: 4^k + 3 * 2^k + 1)

• Hibbard - 1 + 2^0, 1 + 2^2, 1 + 2^4, ...

• Papernov & Stasevich - 2^k - 1

• Pratt - 1, 3, 5, 7, 9, 11, ... (all numbers of the form 2^i * 3^j)

Heap Sort

• Improved selection sort

• Tree node for two child nodes

Heap Sort Complexity

• Best - O(n log n)

• Worst - O(n log n)

• Average - O(n log n)

Heap Sort Algorithm

1. Build a Max Heap: Rearrange the array into a binary heap structure, where the root node is the largest element

2. Swap the root with the last element: Once the heap is built, swap the root (maximum) element with the last element in the array

3. Reduce the heap size: After swapping, the last element is considered sorted, so reduce the heap size by one

4. Heapify the root: Restore the heap property by heapifying the root element, ensuring the subtree rooted at the root is still a valid max heap

5. Repeat until the heap size is 1

Merge Sort

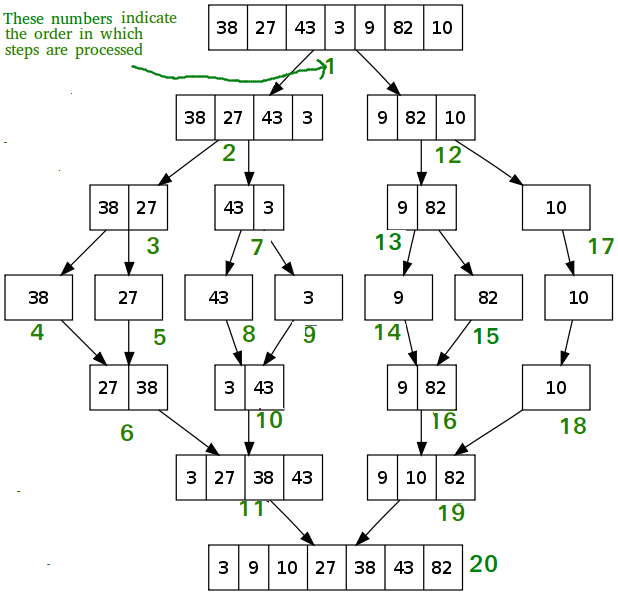
• Divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves

• Uses a merge function to merge two halves

Merge Sort Complexity

• Best - O(nLogn)

• Worst - O(nLogn)

• Average - O(nLogn)

Merge Sort Algorithm

Quick Sort

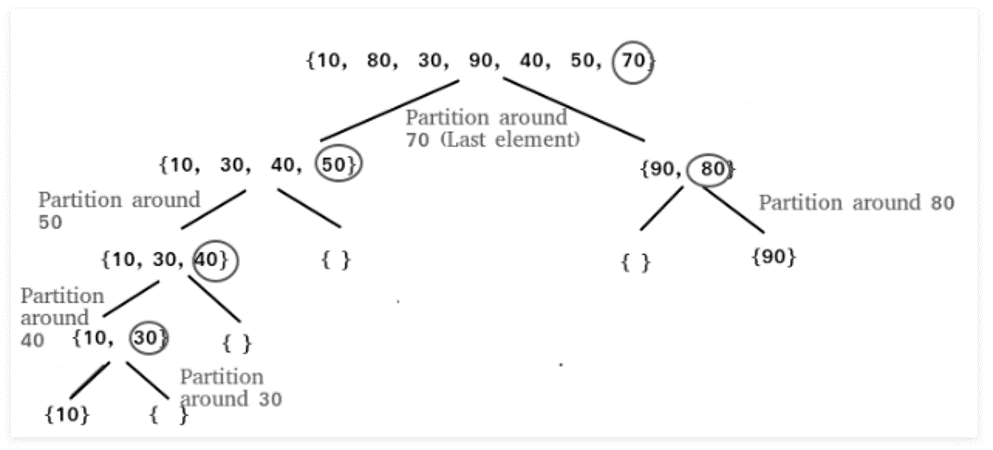
• Picks an element as a pivot and partitions the given array around the picked pivot

Quick Sort Complexity

• Best - O(n log n)

• Worst - O(n^2)

• Average - O(n log n)

Quick Sort Algorithm

Quick Sort Pivots

• First element as a pivot

• Last element as the pivot

• Random element as a pivot

• Median as a pivot.

Bin/Bucket Sort

• Divides the array into several buckets with ranges

Bin/Bucket Sort Algorithm

Bin/Bucket Sort Complexity

• Best - O(n + buckets)

• Worst - O(n^2)

• Average - O(n + buckets)

Queue

• An n ordered list in which all insertions take place at one end, the rear, while all deletions take place at the other end, the front

• Linear data structure

• FIFO structure

Enqueue

• Inserts queue element to the right (back, end)

Dequeue

• Removes queue element from the left (front, start)

enqueue()

public void enqueue(T data)

dequeue()

public T dequeue()

peek()

public T peek()

isEmpty()

public boolean isEmpty()

size()

public int size()

Radix Sort

• Used to sort a list of integer numbers in order

• Counts digits, then compares per digit, starting from the ones digit

• Replaces blanks with zeroes (Ex. 1, 12, 150 → 001, 012, 150)

Radix Sort Complexity

• Best - O(n * digits)

• Worst - O(n * digits)

• Average - O(n * digits)

Radix Sort Algorithm

1. Define 10 queues each representing a bucket for each digit from 0 to 9

2. Consider the least significant digit of each number in the list which is to be sorted

3. Insert each number into their respective queue based on the least significant digit

4. Group all the numbers from queue 0 to queue 9 in the order they have inserted into their respective queues

5. Repeat from step 3 based on the next least significant digit

6. Repeat from step 2 until all the numbers are grouped based on the most significant digit

Queue

Implements Linked-List

Types of Queue

• Queue

• Priority Queue

Priority Queue

• Binary heap queue