STSCI 2150: Final Review

Spring 2024 Final Review

Details on paired design

• Data from the two groups are paired

• Each member of the pair shares much in common with the other, except for the grouping

• There is a one-to-one correspondence between the individuals in the two groups

• One member gets one treatment, the other gets something else

In paired comparisons, we use what to compare?

We use the mean of the difference between the two members of each pair

What do d-bar and μ_d represent?

d-bar: mean of the differences; average of all paired differences

μ_d: the parameter that is in our hypothesis

For paired design, what are the three types of inference about the true difference between elements of a pair, μ_d?

1. Point estimate of μ_d: d-bar

2. Interval estimate of μ_d

3. Hypothesis Test: “Paired t-test”; H₀: μ_d = 0

What is μ_d?

μ_d is the population mean difference between the 1st element and 2nd element of each pair

What is the best point estimate of μ_d?

The sample mean of differences (d-bar)

Null and alternative hypothesis for paired t-test

H₀: μ_d = 0

H_A: μ_d ≠ 0

What is the test-statistic formula for a paired t-test?

How do you find the critical value of t?

t_{alpha(2), df}

When do we reject with critical value?

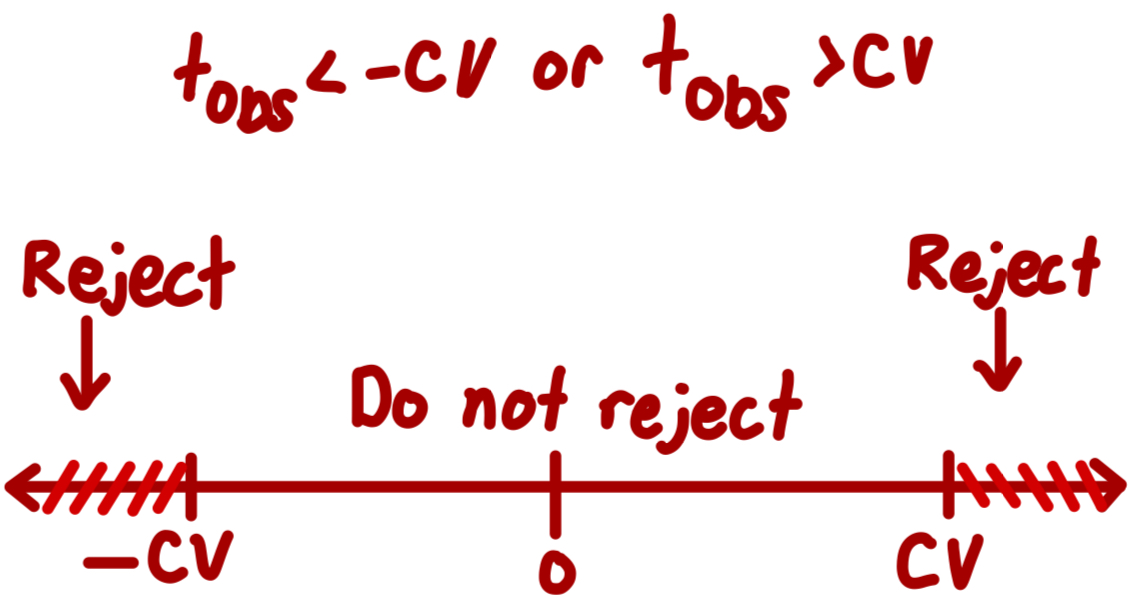
What is the r-code to find p-value and critical value?

P-value: pt(t_obs, df)

Critical Value: qt((1-(alpha/2)), df)

What is the E step of TUNA TEA for paired t-test?

1. Null Distribution: t_obs has t-distribution with n-1 df (where n: number of pairs)

2. P-Value or Critical-Value: do one or other, not both

3. Decision

4. English

What are the assumptions of paired t-test and confidence interval for μ_d?

1. The sample is a random samples of pairs

2. Distribution of the differences in the population has a normal distribution

What is the confidence interval for μ_d?

Confidence interval for the mean of differences of two groups

Note: This is not inference about the difference of means

What is the formula for the confidence interval for μ_d?

Conclusion for confidence interval for μ_d

We are 95% confident that the true mean difference between ___ and ___ is between ___ and ___

What is an ANOVA Test?

ANOVA (Analysis of Variance): used to test the equality of three of more means

Context for ANOVA Test

1. Outcome variable is continuous (“numerical”)

2. More than two groups

3. Want to compare population means

For an ANOVA Test, what test statistic and distribution do we use?

Compare F-test statistic to an F distribution

What happens when we get a large F-Value? What about small F-value?

• When F-value is large, reject the null hypothesis

• When F-value is not large, do not reject the null hypothesis

What are the null and alternative hypothesis for an ANOVA test?

H₀: Population means of all groups are equal (μ₁=μ₂=μ₃)

H_A: At least one mean is not equal to the rest

ANOVA Test Assumptions

1. The observations should be independent within and between groups and should be a random sample from the corresponding population

2. The observations within each group should be nearly normal. Especially important when the sample sizes are small

3. The variability within each group should be about equal to variability in other groups. Especially important when the sample sizes differ between groups

What is the formula for the test statistic of ANOVA tests?

What do large test statistics lead to? What if the P-value is small enough?

• Large test statistics lead to small P-values

• If the P-Value is small enough, H₀ is rejected. Then we conclude that the population means are not all equal

What do you need in order to obtain a large F statistic?

In order to obtain a large F statistic, variability between group sample means needs to be relatively greater than variability within each group

What is total variability?

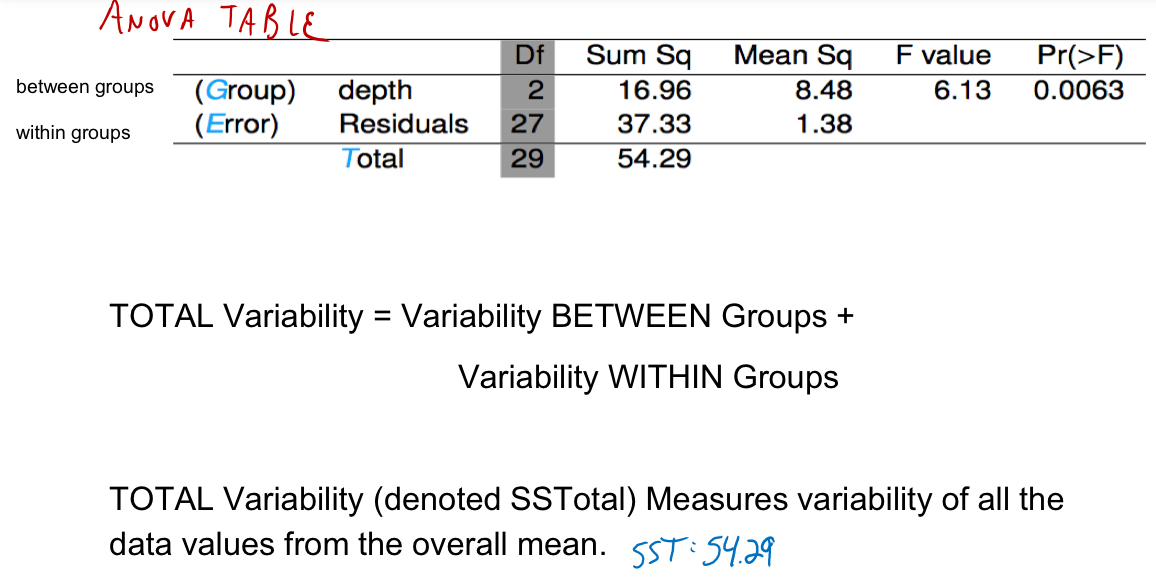
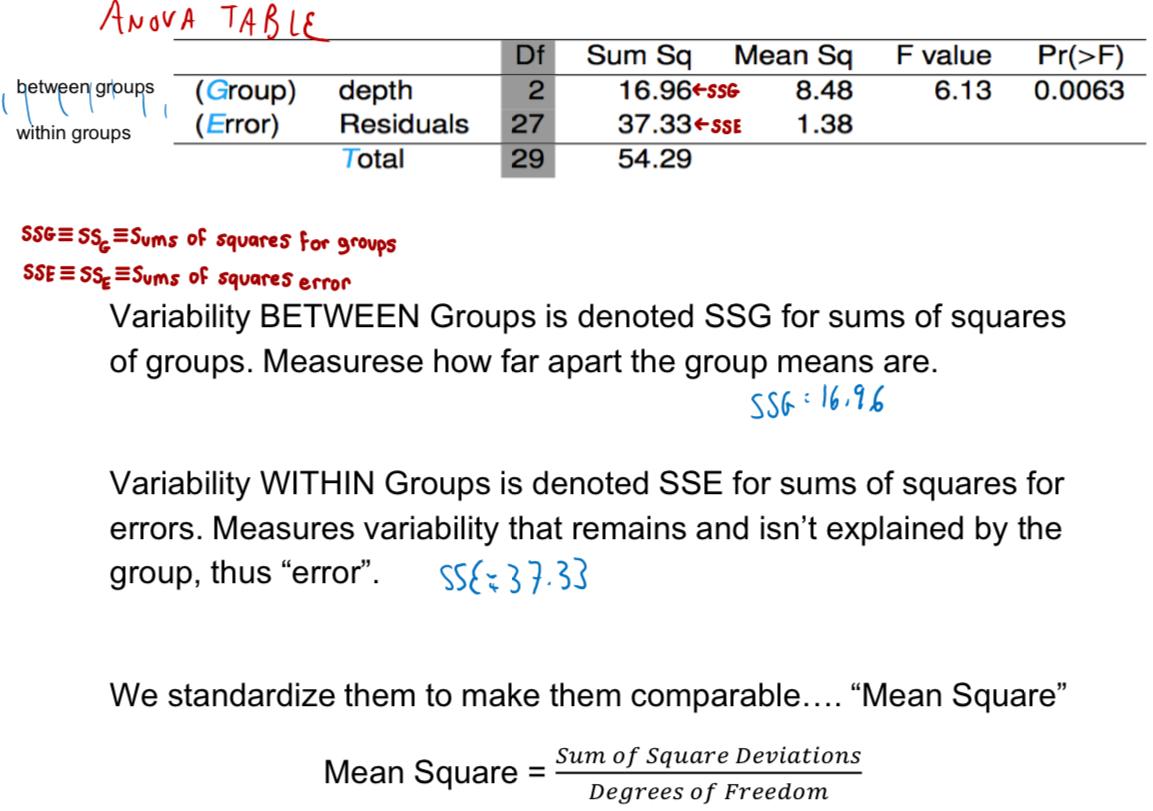
What is SSG and SSE? What is the formula for mean square?

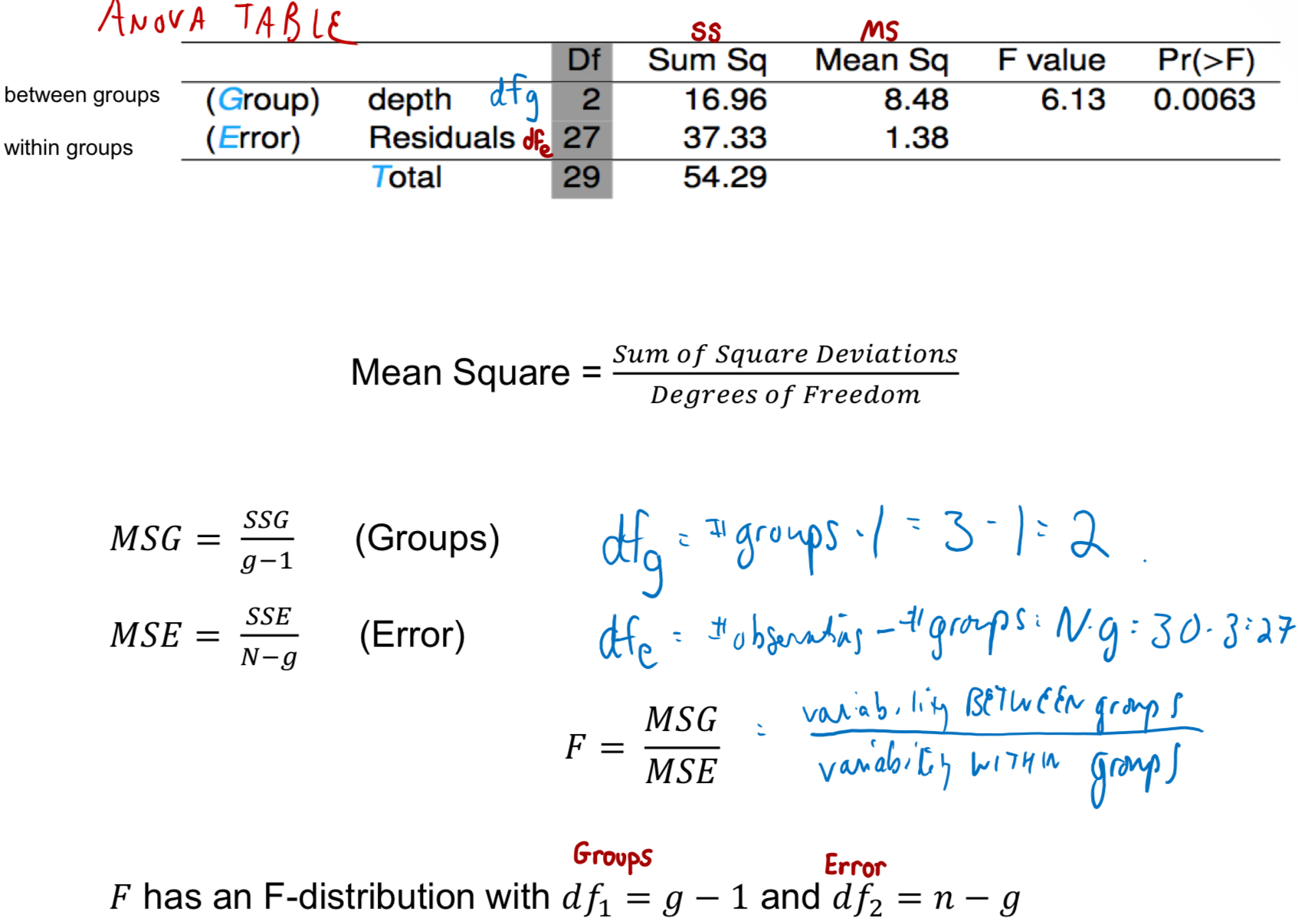
How do you calculate mean square, MSG, MSE, F, and degrees of freedom?

How is mean square error calculated?

Calculated as sum of squares divided by the degrees of freedom

What is the T of TUNA TEA for ANOVA?

What is the formula for F and degrees of freedom?

g: number of groups

n: total number of observations

What is the R-code for p-value and critical value?

1-pf(test statistic, df1, df2)

qf(1-alpha, df1, df2)

Note: qf() is one-sided always. df1 is numerator df and df2 is denominator df

How do you use an F-table?

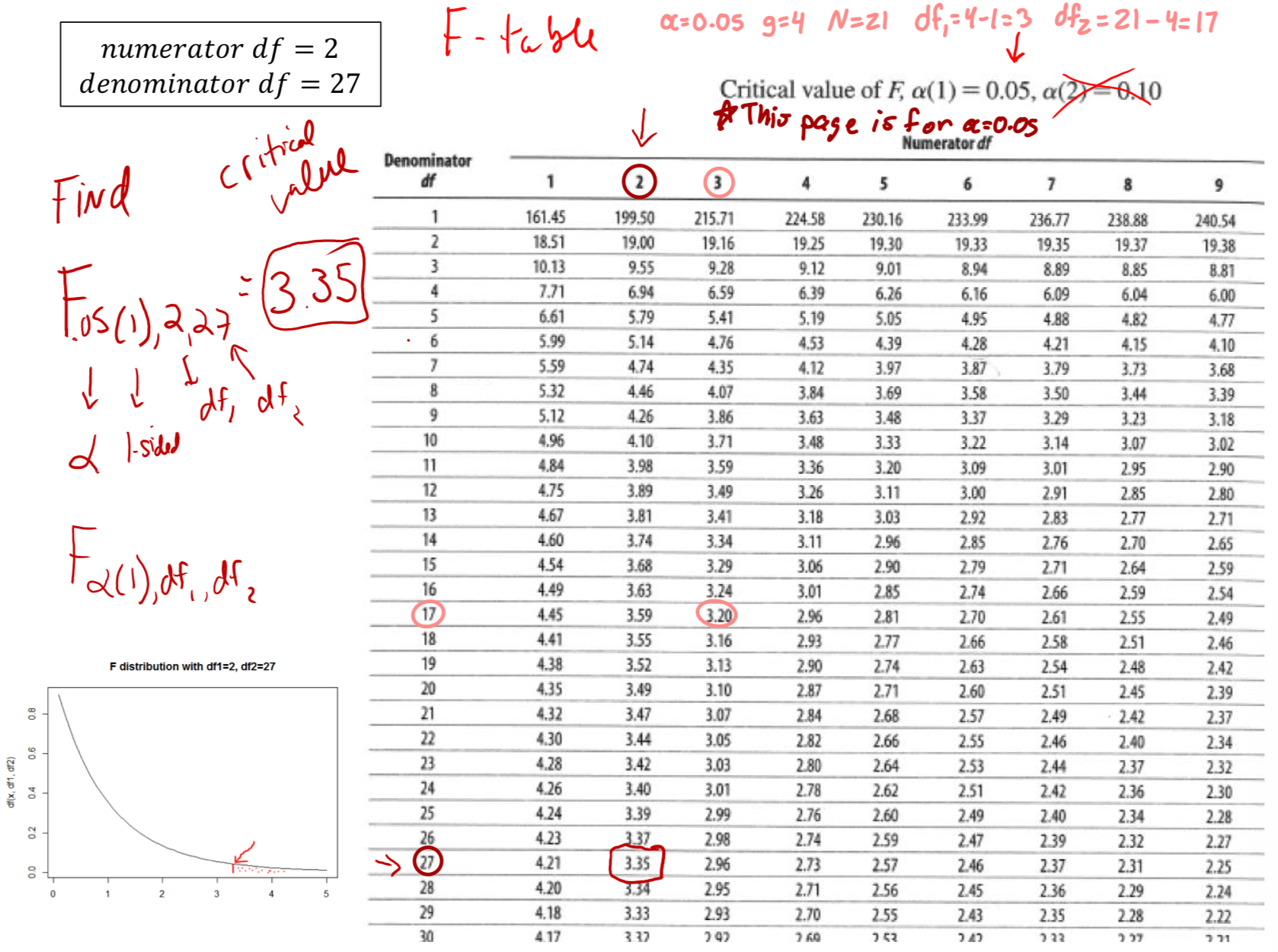
What is the null distribution for ANOVA?

F distribution with df=# and df=#

What are the three assumptions for ANOVA?

1. The observations should be independent within and between groups and should be a random sample from the corresponding population

2. The observation within each group should be nearly normal. Especially important when the sample sizes are small

3. The variability within each group should be about equal to variability in other groups. Especially important when the sample sizes differ between groups

How can you assess if the observations are independent and random samples?

Read about study design

How can you assess approximately normal data?

Graphs

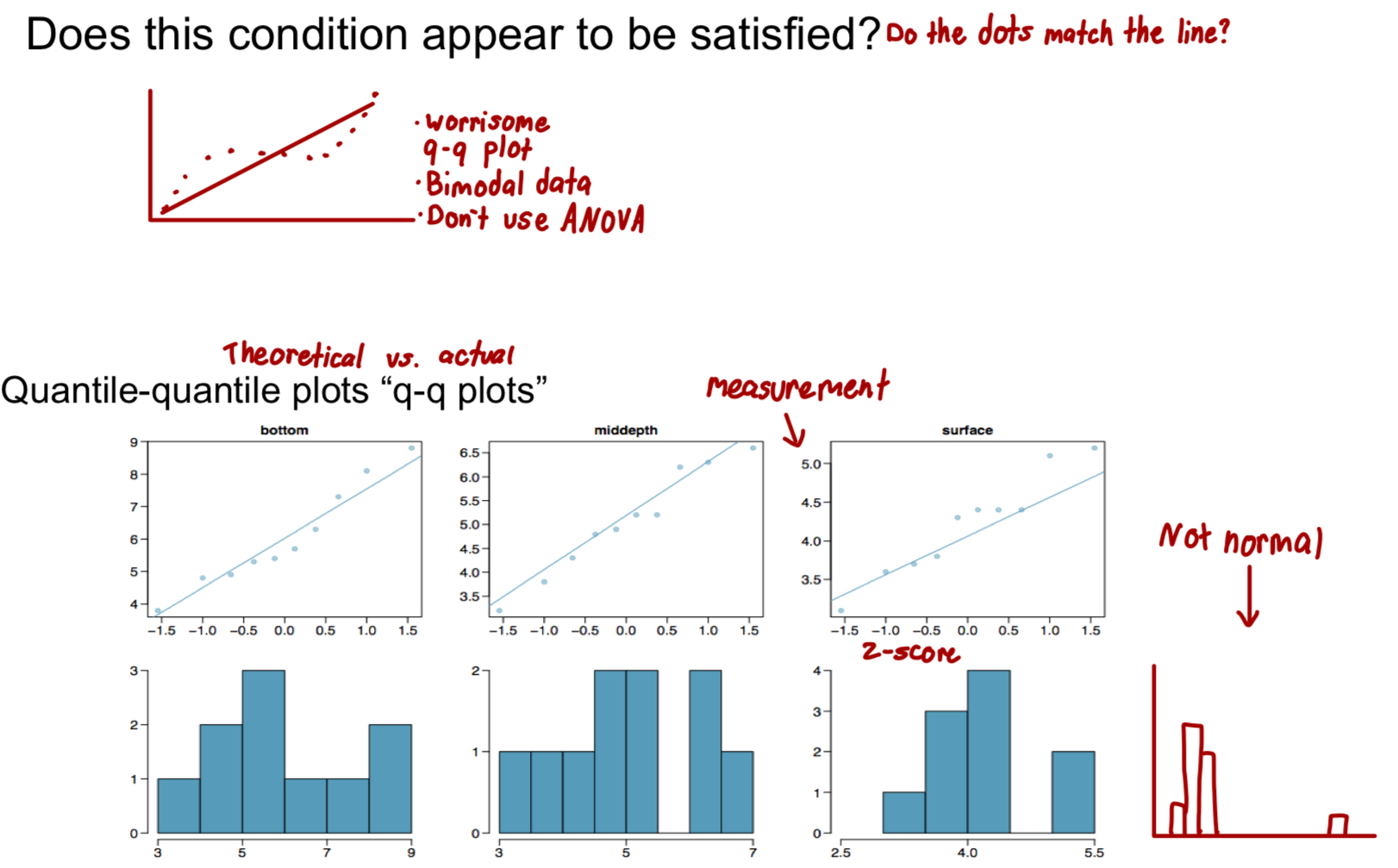
How can you asses equal variances?

Levene’s Test

ANOVA conclusions

• If P-value is small (less than alpha), we reject the null hypothesis. The data provide convincing evidence that at least one mean is different from the others (but we can’t tell which one)

• If P-value is large, we fail to reject the null hypothesis. The data do not provide convincing evidence that at least one pair of means are different from each other

What is the situation after ANOVA test?

• If null is not rejected → do nothing more

• If null is rejected → figure out why

If the means do differ, why can we not do a two-sample t test for differences in each possible pair of groups?

• Inflates type I error

• Difficult

• Time consuming

What is the preferred method as an alternative to multiple t-tests?

Tukey HSD Intervals

What does multiple comparisons refer to?

The scenario of testing many pairs of groups

What does the Bonferroni correlation suggest?

Suggests that a more stringent significance level is more appropriate for multiple comparisons

• a* = a/K, where K is the number of comparisons being considered (get new alpha)

If there are g groups, then what?

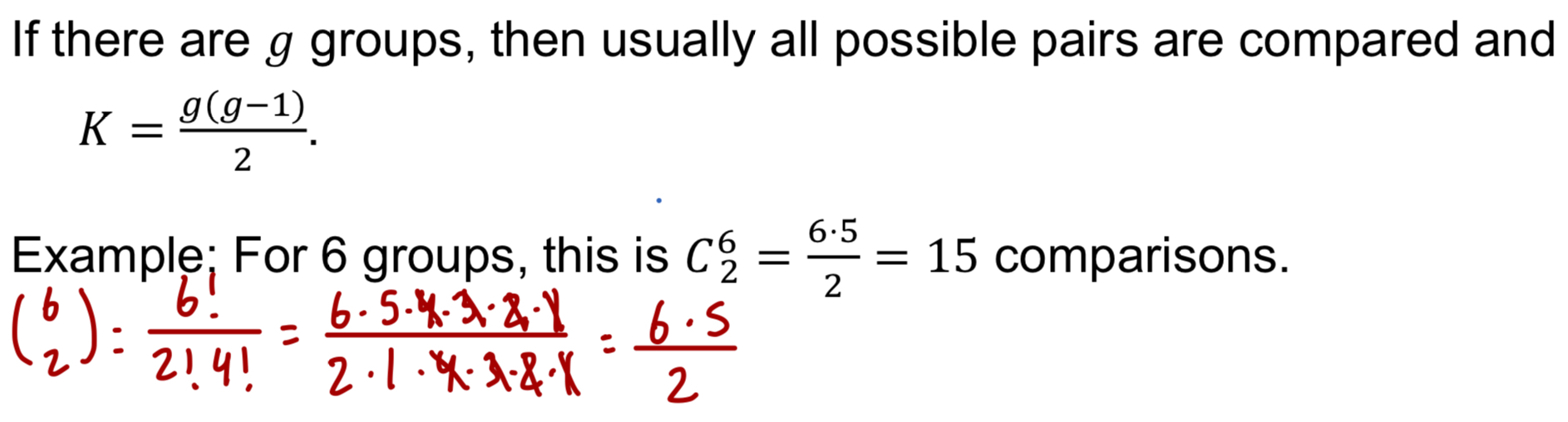
For pairwise comparisons, when at least two means are different, what do we do?

• Use Tukey HSD intervals that control for family-wise confidence levels

• Tukey Honestly Significant Difference or “Tukey-Cramer“

What are conclusions for Tukey HSD?

What do Tukey-Kramer intervals assure? What does this mean?

• Use Tukey-Kramer intervals, which assure a 95% family-wise confidence level for all pairwise confidence intervals

• A 95% family-wise confidence level means that the chances of at least one Type I error is 5%, for the entire set of confidence intervals (controls for Type I error)

What is the context regarding correlation?

Context: we use correlation with 2 numerical variables

What is correlation?

Quantifies the strength and direction of the linear relationship between two numerical variables

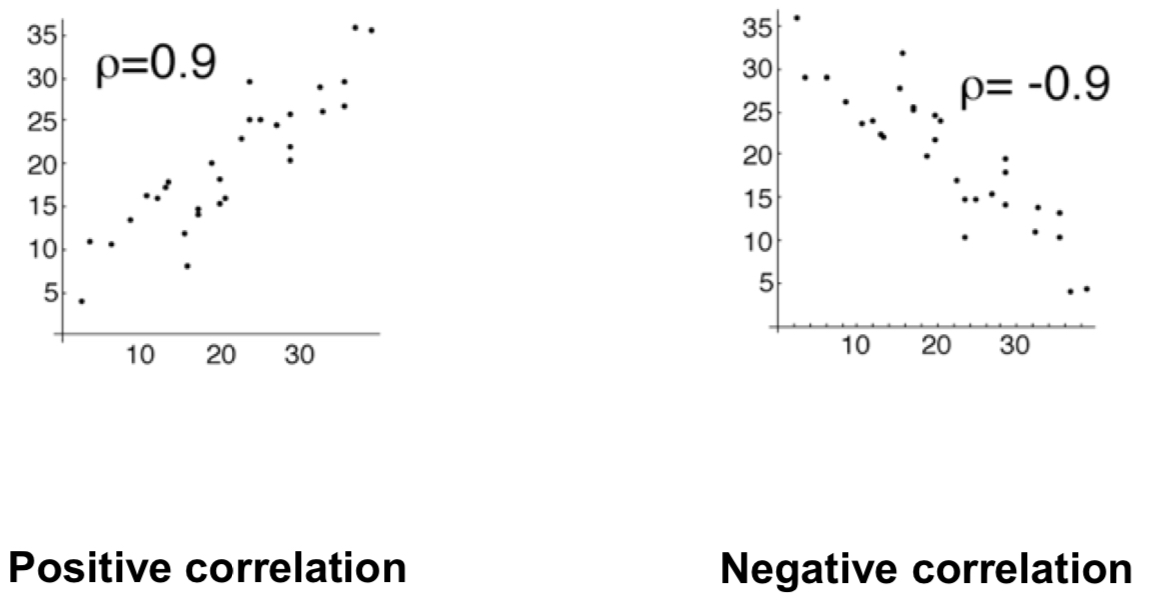
• Strong vs weak

• Positive vs negative

What are the graphs for positive correlation and negative correlation?

What is r?

• Correlation: r

• r is called the “sample correlation coefficient

• Numerically describes the linear relationship between two numerical variables. It is a number, calculated from the data

What is the range of values for r? What are the interpretations?

What is the assumption for correlation?

Bivariate Normal

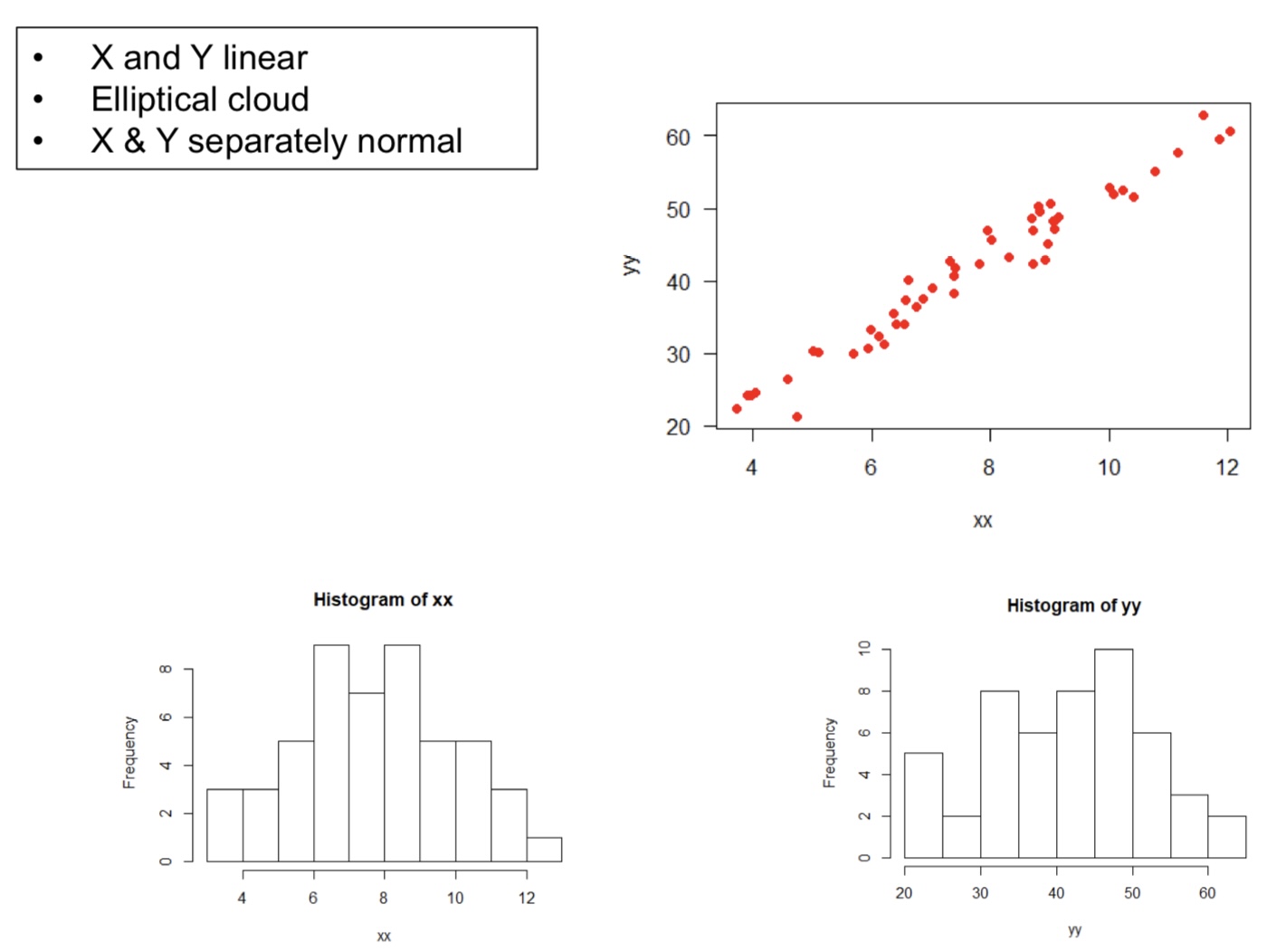
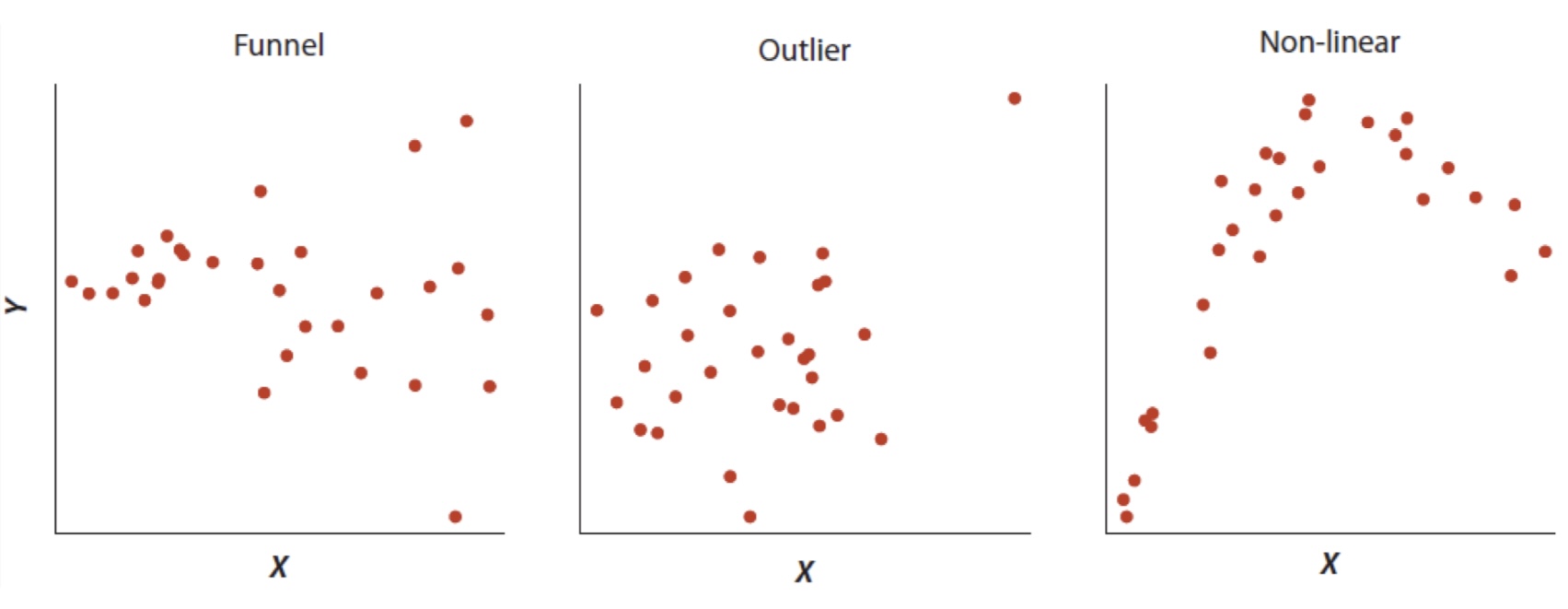
What are some common deviations from bivariate normal?

What is correlation? What does correlation measure? What is there a stronger association between? What does correlation not imply?

• It is single number, and the sign of r (+ or -) gives direction of association

• Correlation measures the strength of the linear association between two variables

• Stronger association between x and y

  • r is larger in magnitude, that is, closer to +1 or -1

  • knowing x helps more in predicting y & vice versa

• Correlation does not imply causation

What are some correlation common errors?

• Error: Assuming that correlation implies causation

  • Truth: correlation can result from many circumstances, of which causality is only one

• Error: Failing to distinguish between correlation, which is linear, and association, which can be strong but possibly nonlinear

  • Truth: These are two different, but related topics

If two variables are correlated, what does it not mean?

• Just because two variables are correlated, does not mean that one causes the other

• Correlation is not causation

Correlation vs regression

• Correlation quantifies the linear relationship between two variables

  • It is a number and has its uses

• More powerful tool: Linear Regression

• Both quantify relationships between 2 variables

  • Correlation: a number, used for just two variables

  • Regression: an equation, predicting Y and X, used with two or more vairables

What is the intuitive approach for regression?

Two variables change together

What is the context for regression?

• Two numerical variables, with a linear relationship

  • Can we use one to predict the other?

• Need to do a test of significance to officially determine this

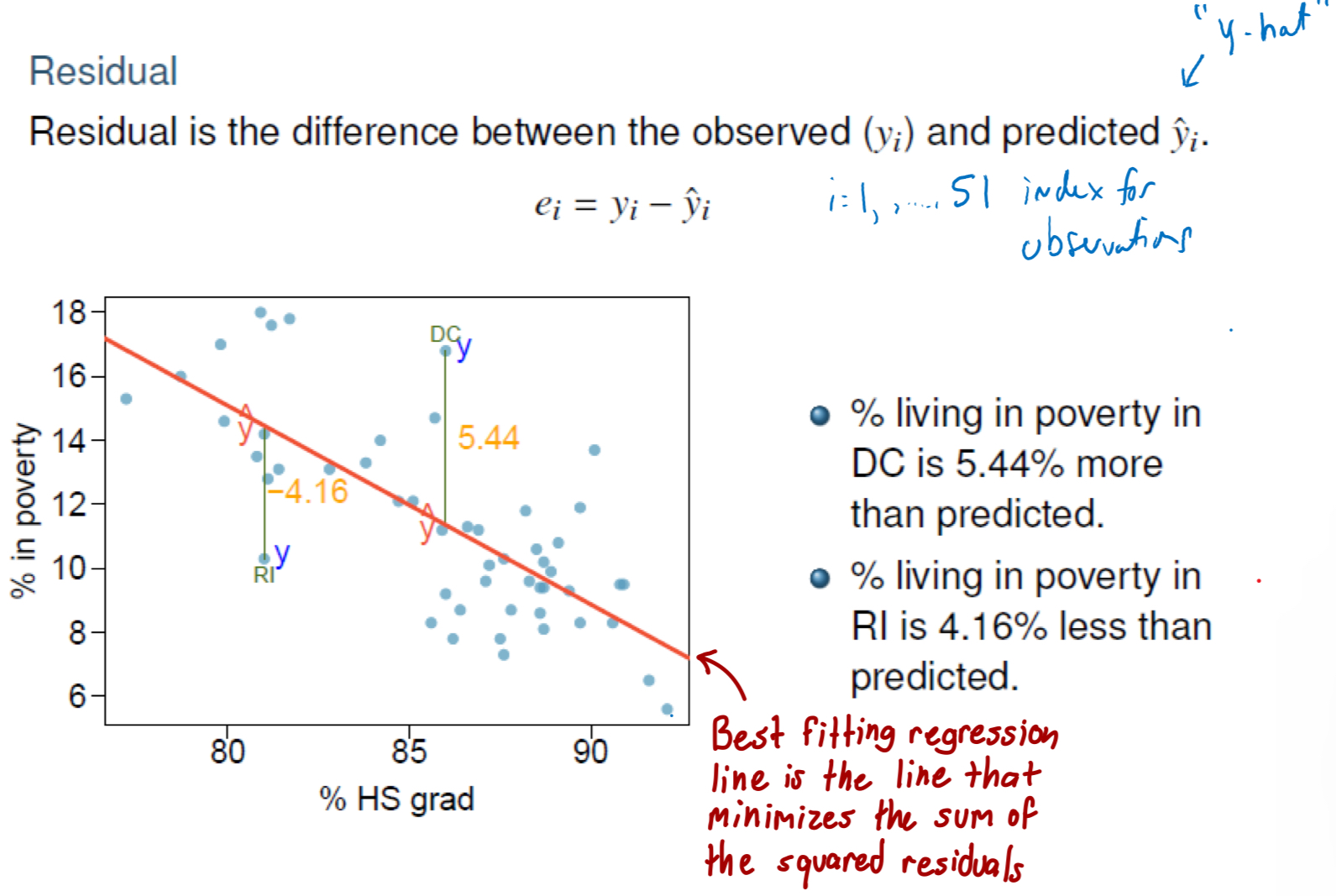
What are residuals?

The difference between the observed (y_i) and predicted y_i-hat

What is the formula for fitted regression line?

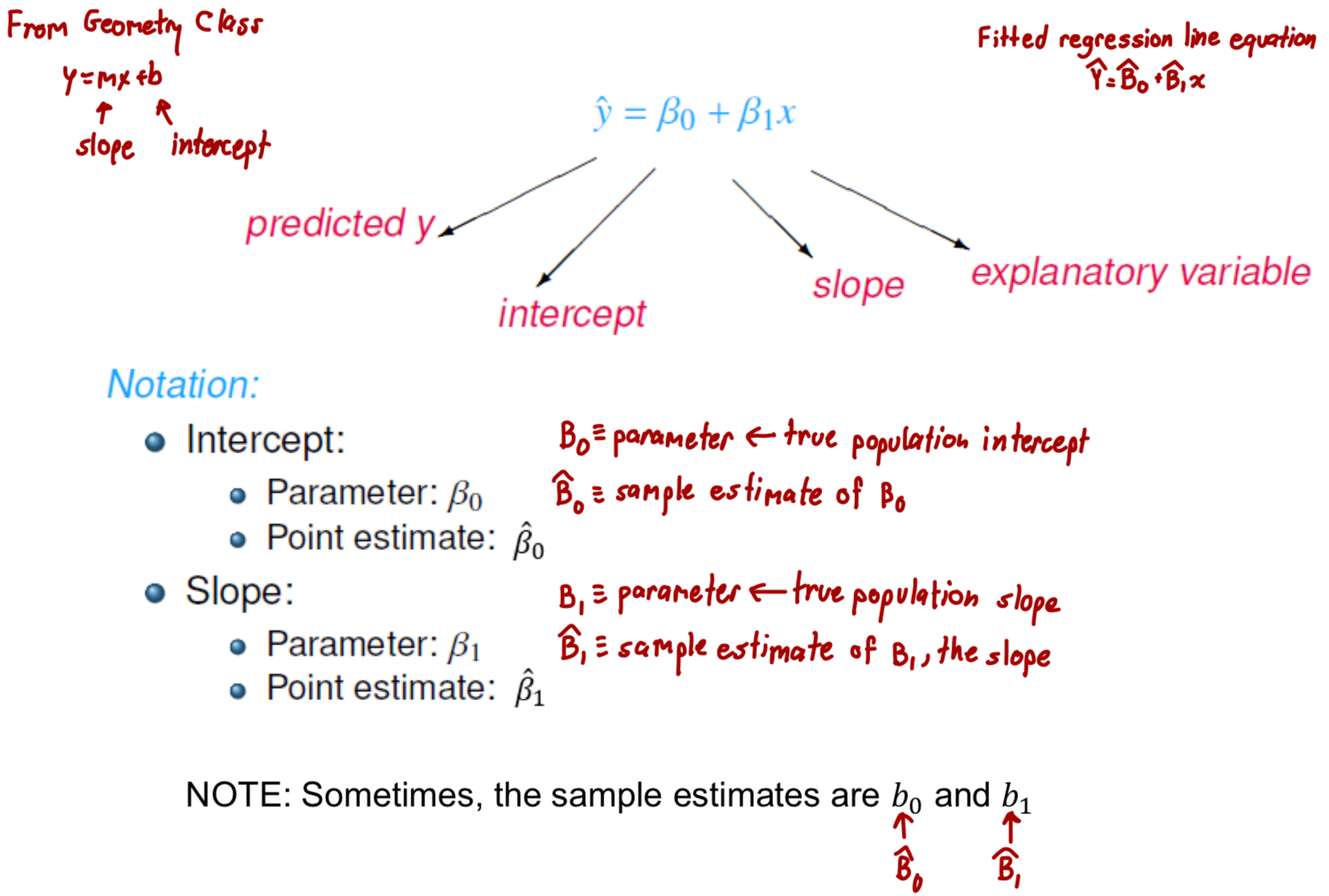
Interpret intercept and slope

• Intercept: when x=0, y is expected to equal the intercept

• Slope: for each unit in x, y is expeted to increase/decrease on average by the slope

General form for slope interpretation

A 1 unit increase in “x-variable” is associated with a “slope” change (increase or decrease) in “y-variable”

What are the assumptions for the least squares line?

1. Linearity

2. Nearly normal residuals

3. Constant variability

We can check these conditions by looking at residual plots

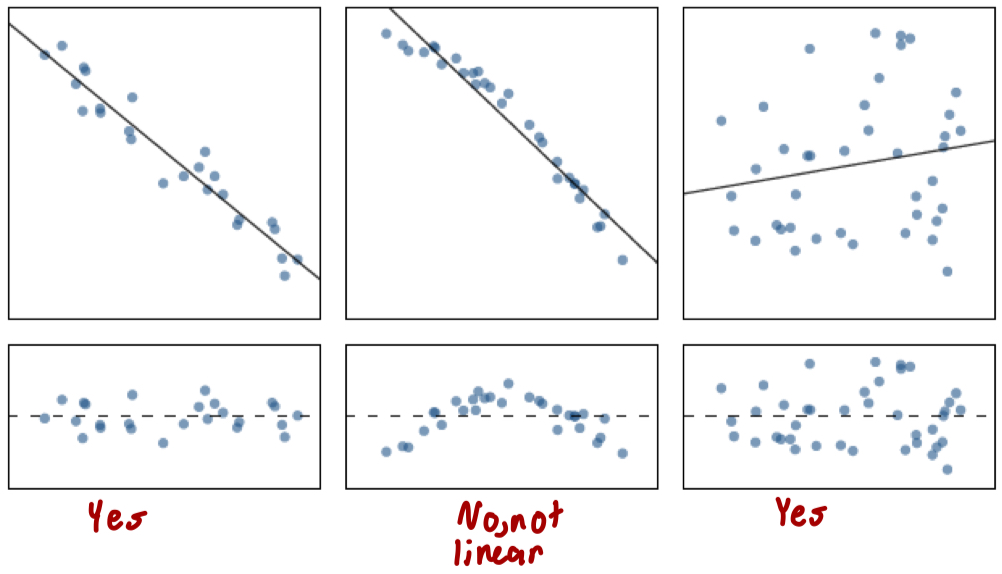
What is linearity and how do we check for it?

• The relationship between the explanatory and the response variable should be linear

• Check using a scatterplot of the data, or a residuals plot

• Residual plot should look like an elliptical cloud of points

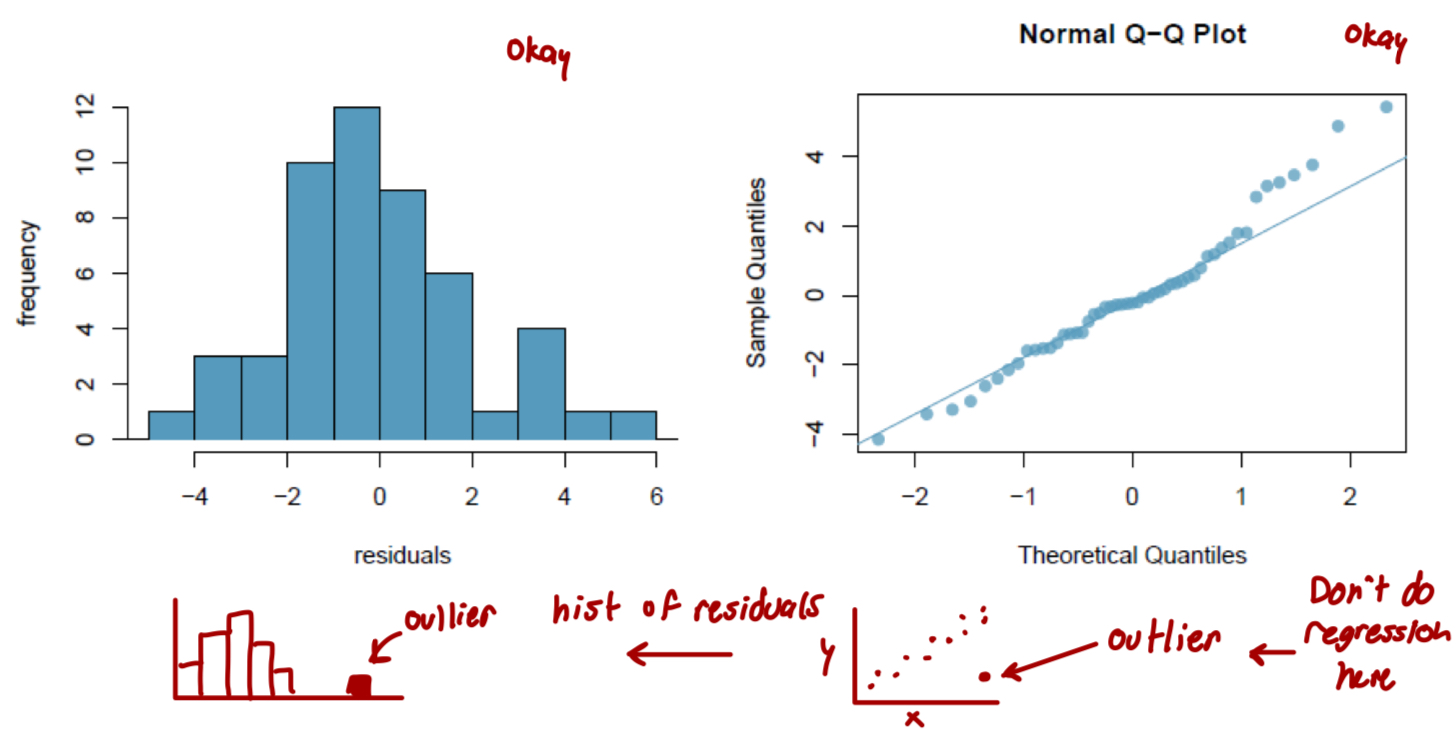
What is nearly normal residuals and how do we check for it?

• The residuals should be nearly normal

• This condition may not be satisfied when there are unusual observations that don’t follow the trend of the rest of the data

• Check using a histogram or normal probability plot of residuals

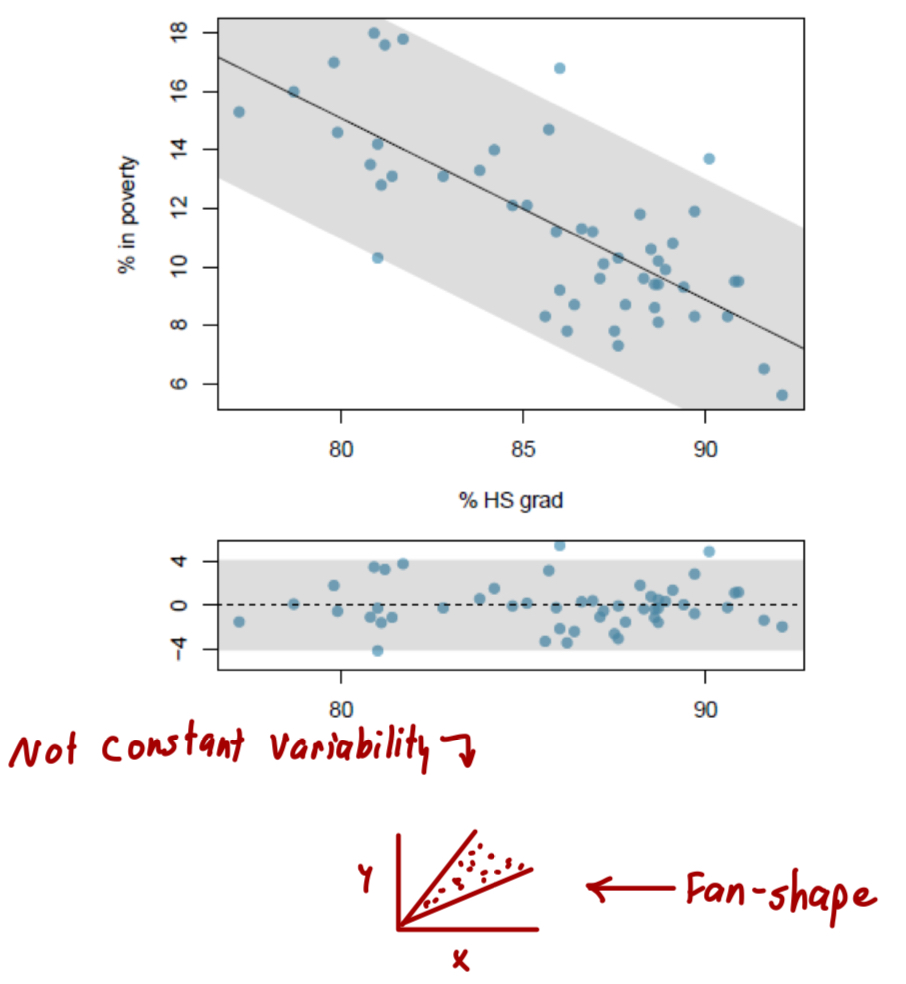
What is constant variability and how do we check for it?

• The variability of points around at least squares line should be roughly constant

• This implies that the variability of residuals around the 0 line should be roughly constant as well

• Also called homoscedasticity

• Check using a histogram or normal probability plot of residuals

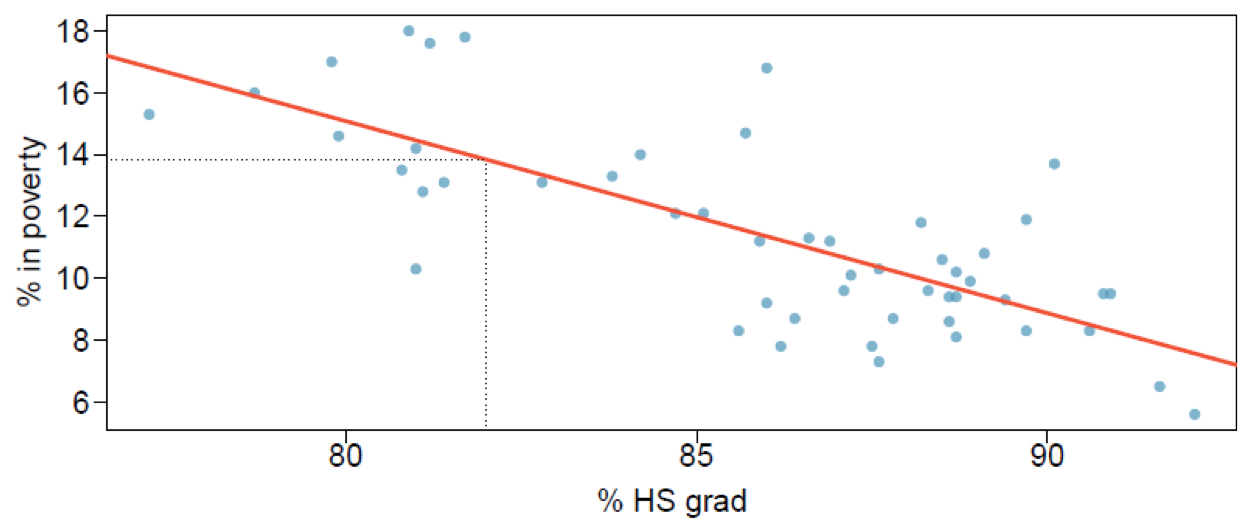
What is prediction? Will there be some uncertainty associated with the predicted value?

• Using the linear model to predict the value of the response variable for a given value of the explanatory variable is called prediction, simply by plugging in the value of x in the linear model equation

• There will be some uncertainty associated with the predicted value

Correlation vs slope

• Slope: how steep

• Correlation: how tightly the points cluster around a prediction line

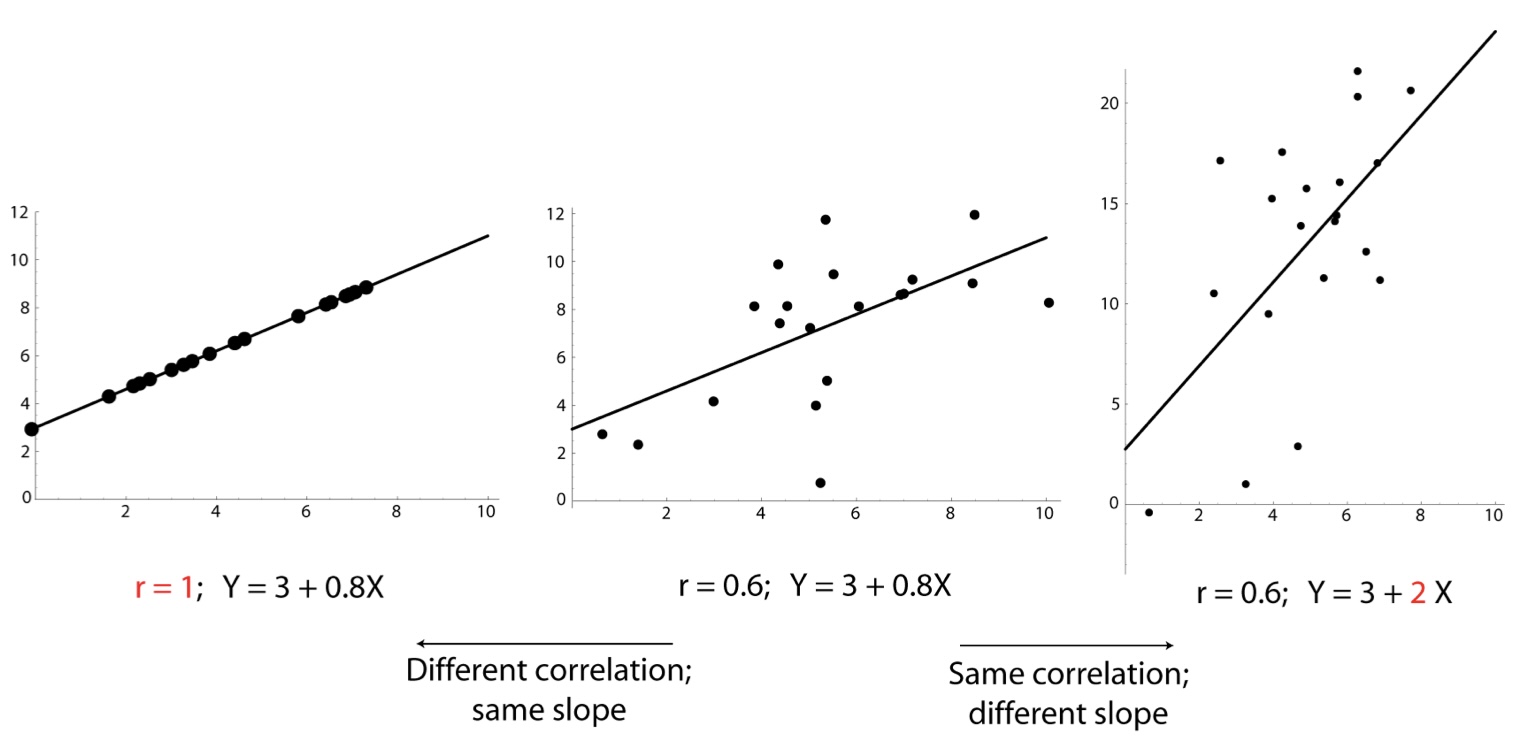
How do we determine how strong the linear relationship between X and Y is?

Use the summary statistic, R² (correlation coefficient)

What is R²? How is R² calculated as? What does R² tell us? What is the remainder of the variability explained by?

• The strength of the fit of a linear model is most commonly evaluated using R²

• R² is calculated as the square of the correlation coefficient

• It tells us what percent of variability in the response variable is explained by the model, or by the predictor variable

• The remainder of the variability is explained by variables not included in the model or by inherent randomness in the data

General conclusion for R²

With R²= __, this implies that __x100% of the variability in “y-variable name” is explained by “x-variable name”

If high, then strong relationship

What is extrapolation? What might the intercept sometimes be?

• Applying a model estimate to values outside of the realm of the original data is called extrapolation

• Sometimes the intercept might be an extrapolation

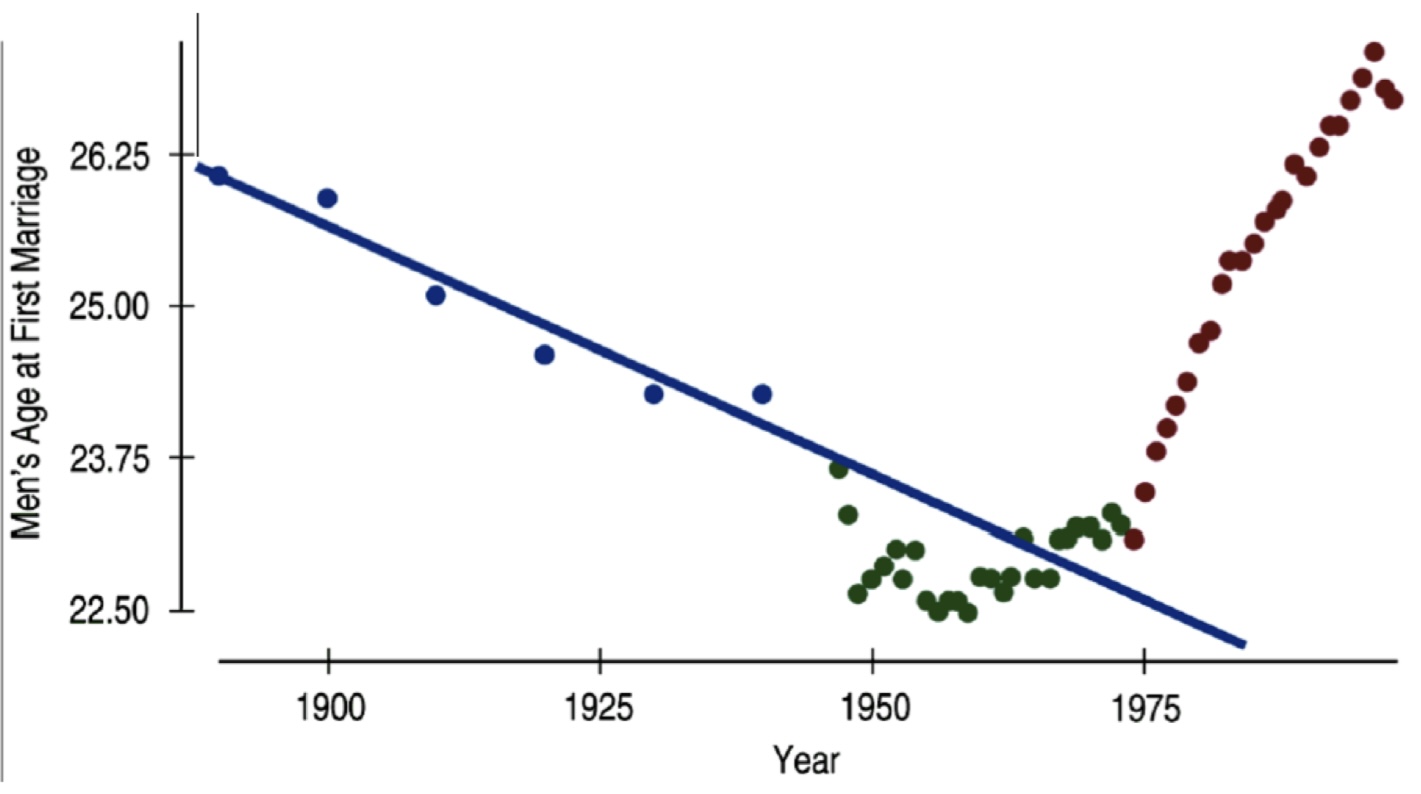
Define extrapolation. What do you need to be aware of with extrapolation?

• Definition: prediction made beyond the range of values in the data

• Beware: predictions are only valid within the range of values of the predictor variable that were used to fit the model

Why should we conduct a hypothesis test of the slope parameter?

• Goal: Assess whether or not a predictor is “good” at predicting an outcome or not

• This is a test of predictor variable’s coefficient

What is the null and alternative hypotheses for test of regression slope?

H₀: ___ is not a good predictor of ___ (B₁ = 0)

H_A: ___ is a good predictor of ___ (B₁ ≠ 0)

T Step of TUNA TEA for test of regression slope

E Step of TUNA TEA for regression slope

What is the p-value and critical level R-codes for regression slope?

P-Value: 2(1-pt(t-stat, df))

Critical Value: qt((1-(a/2)), df)

What does linear regression describe? What can it be used to determine? How many variables can it have? What does the slope of the regression line indicate?

• Linear regression describes the straight-line relationship between two variables with an equation

• Linear regression can be used to determine if one variable is a good predictor of another

• Linear regression can have two variables with a relationship that is strong or weak and is described by R²

• The slope of the regression line indicates the expected change in Y for a one-unit increase in X

Whats an easy way to check if the linear regression assumptions hold true?

Check if the residual plot have elliptical cloud shape

What can observational studies only find?

Can only find correlations between variables

What does randomization help establish?

Randomization helps establish causality

What are confounding variables?

Unmeasured variable that changes in tandem with one or more measured variable…Gives a false appearance of a casual relationship between the measured variables

How can you assess the relationship between variables and account for (or control for) confounders?

1. Experiments and randomization (for confounders you might not know about)

2. Blocking or stratifying of the confounders you know about

What is blocking? What is it used for?

• Grouping of experimental units that have similar properties; within each group, different treatments are applied to different units

• Used to control for qualities that might or are known to affect outcome

  • Ex: test of fertilizer (yes or no) on plant growth. Humidity and temperature are known to affect plant growth. Thus → do blocking by greenhouse. Randomize to treatment within greenhouse

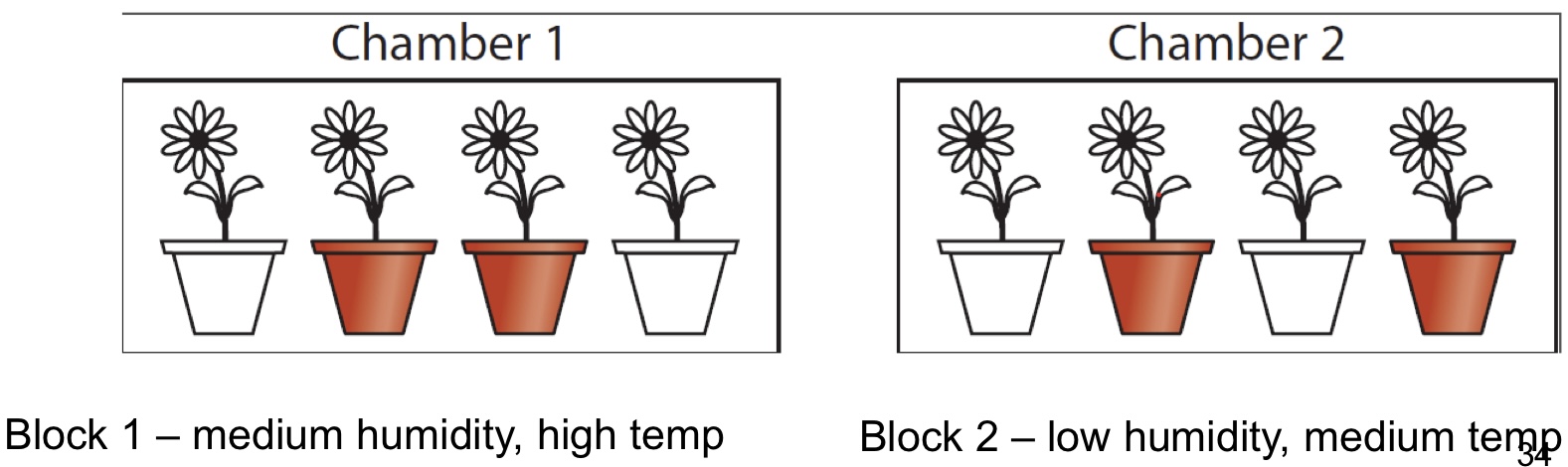
How do you choose a blocking variable?

• Choose a blocking variable that is known or suspected to have an effect on outcome. We “control” for this variable by “blocking”

  • Ex: Greenhouses: Plant growth can be a function of environmental factors such as temperature humidity

    • Block 1: medium humidity, high temperature

    • Block 2: low humidity, medium temperature

• After blocking, randomize to treatment within the blocks

What are the 7 good design features of expeirments?

• Eliminate bias:

  • Controls

  • Random assignment to treatments

  • Blinding

  • Random sample (or correct re-weighting)

• Reduce sampling error (increase precision and power)

  • Replicates (sufficient sample size)

  • Balance

  • Blocking

Is the control group different from the experimental treatment group? What treatment does the control group receive? What is the importance of controls?

• A control group is approximately the same as the treatment group in all respects aside from the treatment itself

• The control receives the “standard treatment”. Could be no treatment or existing treatment

  • Ex: sugar pills = “placebo”

• Importance of controls: need to see what happens with no treatment - may get better by itself (depression, pain, ear infections)

What is randomization?

• The random assignment of treatments to units in an experimental study

  • Ex: Assignment to a week of 8-hour sleep nights vs. 6-hour sleep nights

• This does not mean random sample

What is the most important aspect of study design? What are the best medical studies? What does randomization control for?

• Random assignment is the most important aspect of study design

• Best medical studies are “controlled clinical trials”, which by definition, involve randomization of subjects to treatment groups

• Randomization averages out - “controls for” the effects of confounding variables

What is blinding? What do unblinded studies find much larger of? What is single, double, and triple blind?

• Process of concealing information from participants (and sometimes including researchers) about which subjects receive which treatment

• Unblinded studies find much larger effects (sometimes threefold higher), showing the bias that results from lack of blinding

• Single vs double vs triple blind

  • Single: patient doesn’t know treatment group

  • Double: neither patient or medical providers know treatment group

  • Triple: neither patients, medical staff, or researchers know treatment group

What is random sampling? is this hard to achieve?

• Process of choosing individuals at random and independently from a population

• This can be hard to judge or achieve. Elements of volunteer bias may occur

What are replicates?

• Carry out study on multiple independent objects

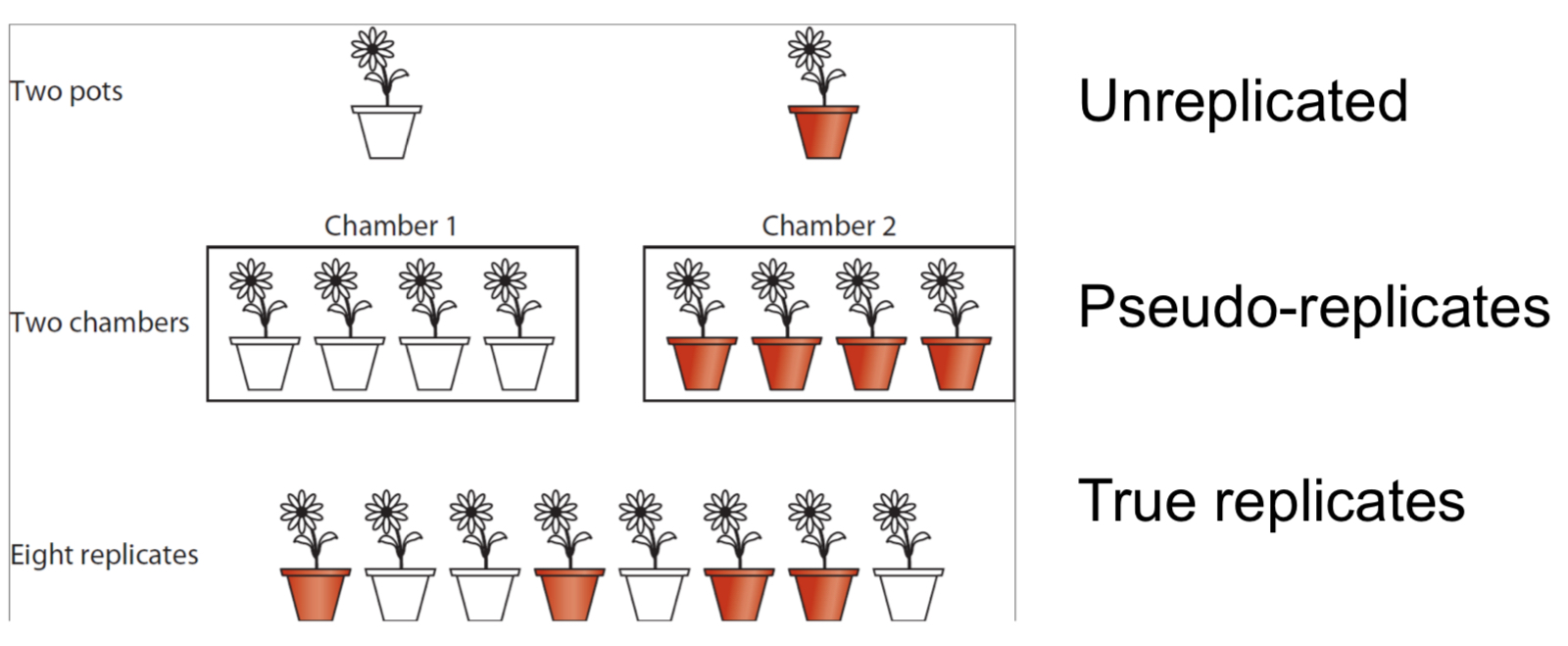
In replicates, does every treatment group have only one individual?

• Every treatment group must have more than one individual

• True replicates are multiple independent units in the experiment in each group

What does balance refer to? What do all the treatments have? What does being balanced reduce? What if your using blocking?

• Nearly equal sample sizes in each treatment

• In a balanced experiment design, all treatments have about equal size - within 10%

• If using blocking, must be within blocks

When are results generalizable to a larger population?

• Yes: if you have drawn a random sample from the larger population

• No: if your sample is not from the larger population

When do results indicate a cause-effect relationship?

• Yes: if you have randomized individuals to the different treatment arms

• No: if your study does not include randomization to treatment