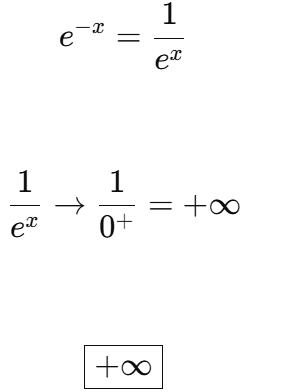CALC Exam 3

Derivative of sinx

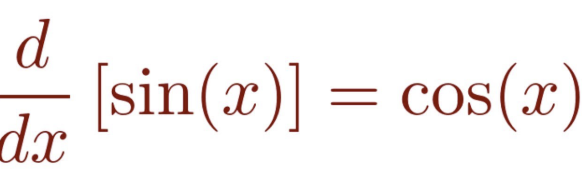
Derivative of cosx

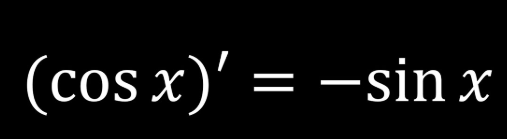
derivative of tanx

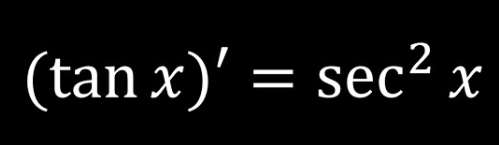
derivative of cotx

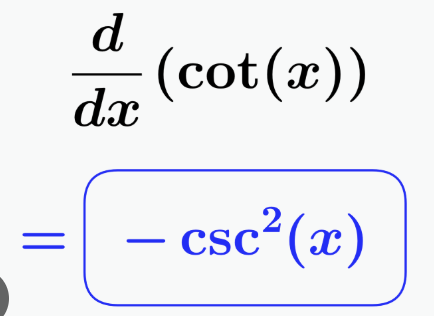
derivative of secx

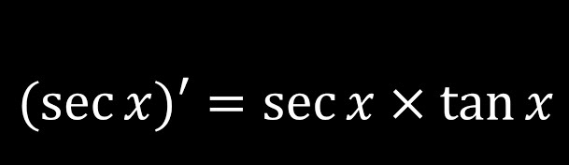
derivative of cscx

derivative of inverse sinx (arcsinx)

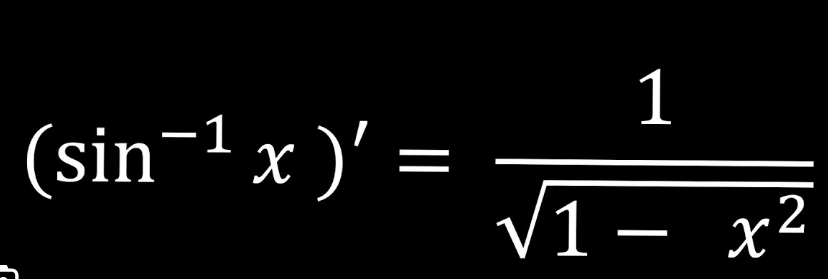
derivative of inverse tanx (arctanx)

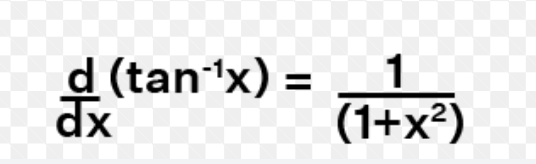
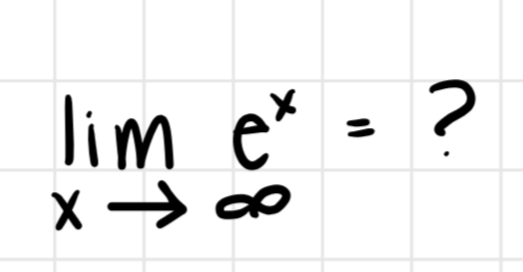
Compute the limit for exponential growth

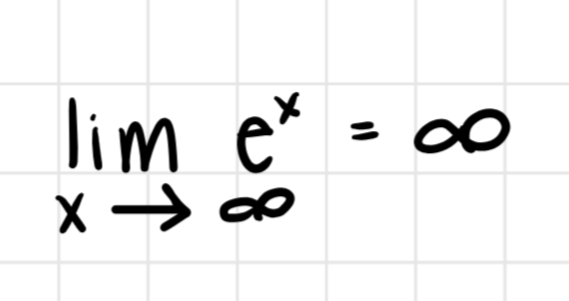
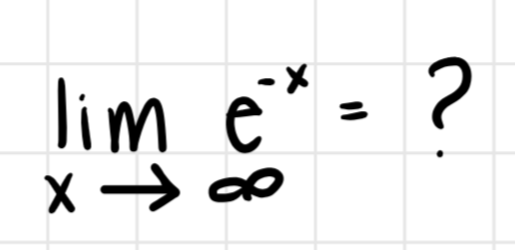
Compute the limit for exponential growth

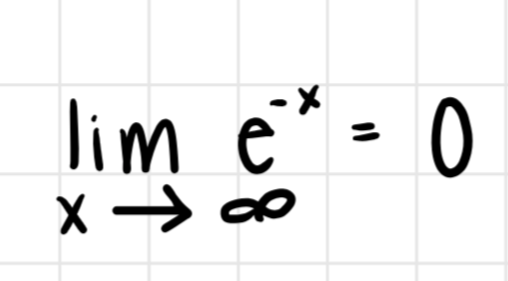
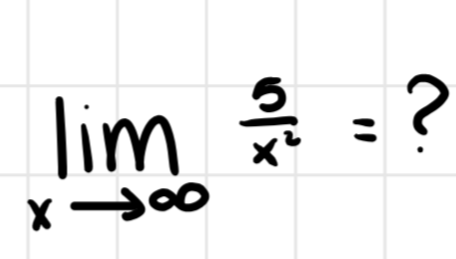
Compute the limit when the denominator grows faster than the numerator such as

limit is 0

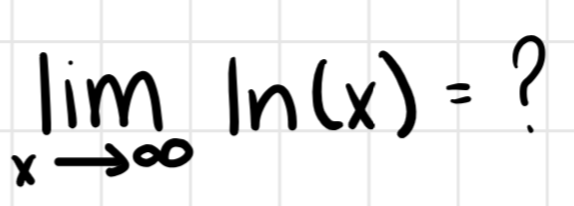
Compute the limit at natural log

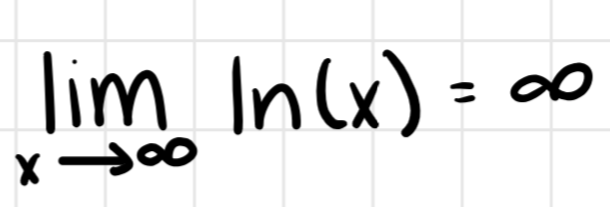
When is a vertical asymptote present

set the denominator equal to 0

when does the horizontal asymptote equal 0 (y = 0)

The degree in the numerator is less than the degree of the denominator

When does the horizontal asymptote bring an actual value (not 0)

If the degree in the numerator is equal to the degree of the denominator

What happens if the degree in the numerator is one greater than the degree in the denominator?

an oblique asymptote may be present and you should use polynomial long division

What are the conditions for Rolle’s Theorem?

If all the conditions in Rolle’s Theorem is true then…

there is at least one value of x, “c'‘, a < c < b where f’( c ) = u

What is the Mean Value Theorem?

If f(x) is continuous on [a,b] and differentiable on (a,b), there's some point where the instantaneous rate of change (derivative) equals the average rate of change over [a,b][a, b][a,b].

Antiderivative of sinx

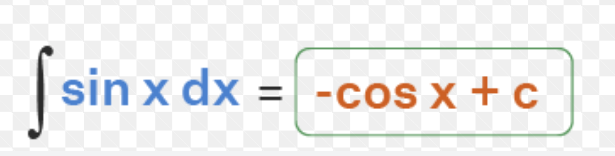
Antiderivative of cosx

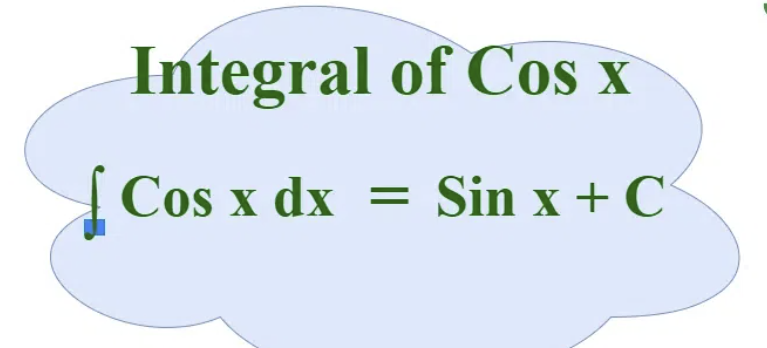
antiderivative of sec²x

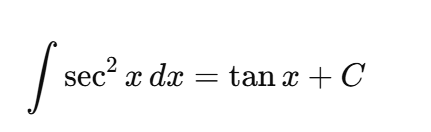
antiderivative of secxtanx

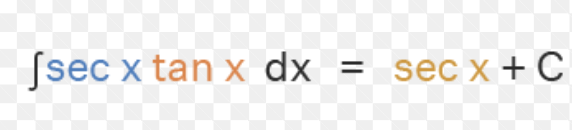
antiderivative of csc²x

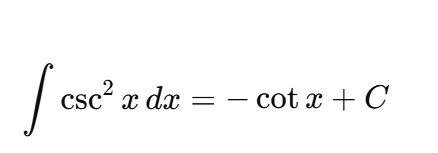
antiderivative of cscxcotx

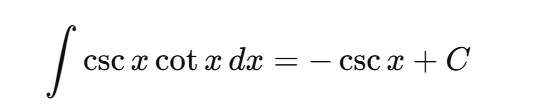
Change of Log Base

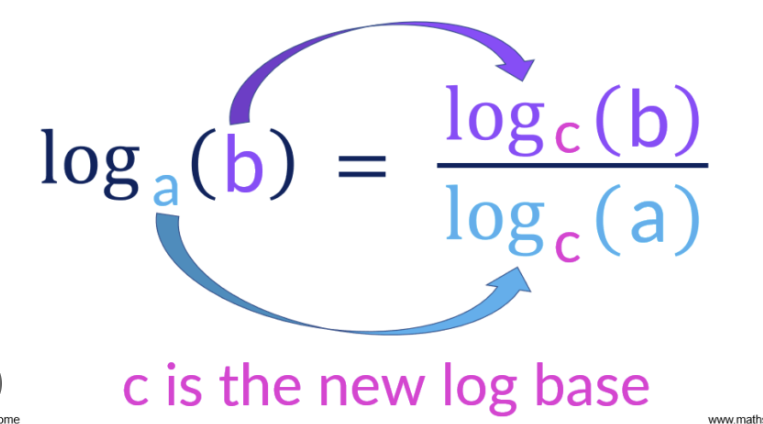
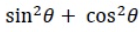
= 1

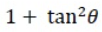
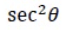
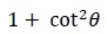
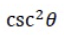
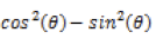
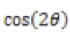
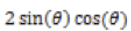
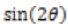
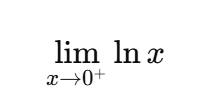
Compute the limit

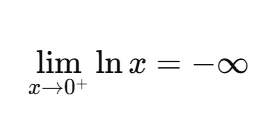
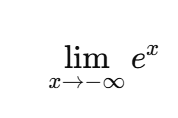
compute the limit

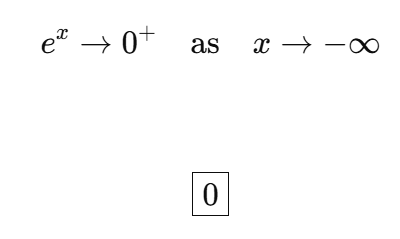
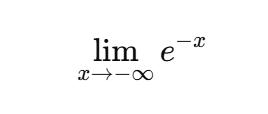
compute the limit