M1110 Lineární algebra I

Flashcards pro přípravu na zkoušku z lineární algebry. PS 2024.

Definuj těleso.

Těleso je algebraická struktura, která obsahuje dvě operace, sčítání a násobení, a splňuje určité axiomy, jako je asociativita, komutativita, distributivita, existence význačných prvků; konkrétně existence neutrálních prvků (0 pro sčítání a 1 pro násobení), opačných a inverzních prvků.

Definuj skalár.

Skalár je prvek tělesa. Jako takový se používá pro násobení vektorů a matic.

Definuj komplexní číslo.

Komplexní číslo je číslo z ve tvaru a + bi, kde a spolu s b jsou reálná čísla a i je imaginární jednotka.

Definuj algebraický tvar komplexního čísla.

Komplexní číslo z v algebraickém tvaru zapisujeme jako z = a + bi, kde a je reálná část komplexního čísla z, b je imaginární část komplexního čísla z, i je imaginární jednotka.

Definuj imaginární jednotku.

Imaginární jednotka je symbol i, který představuje druhou odmocninu z -1. To znamená, že i² = -1.

Jak definujeme sčítání dvou komplexních čísel?

Sečteme nejdříve reálné části a poté komplexní části.

Jak definujeme násobení dvou komplexních čísel?

Podle klasických algebraických pravidel, přičemž i², které vznikne roznásobením můžeme nahradit -1 (dle definice), takže platí:

(a + bi)(c + di) = ac + adi + bci + bdi² = ac + adi + bci − bd = (ac − bd) + (ad + bc)i

Jaké mají komplexní čísla důsledky?

• řešení rovnice x² = −1, konkrétně x = i a x = −i

• možnost řešit kvadratické rovnice s negativním diskriminantem

• zachování všech algebraických pravidel pro sčítání a násobení

Definuj komplexně sdružené číslo.

z¯ = a − bi

Jak je definována absolutní hodnota z?

|z| = odmocnina(a²+b²)

Jaké jsou výhody algebraického tvaru?

• snadná interpretace reálné a imaginární části

• jednoduché sčítání a odčítání

• intuitivní a praktický způsob reprezentace a manipulace s komplexními čísly v matematice a jejích aplikacích

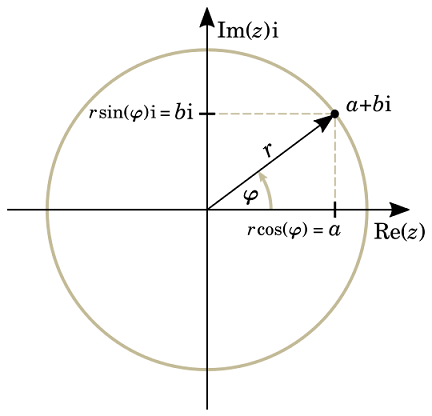
Definuj geometrický tvar komplexních čísel?

Jedná se o tvar, který zdůrazňuje geometrickou interpretaci komplexních čísel. Komplexní císlo z v geometrickém tvaru zapisujeme jako z = r(cos θ + i sin θ), kde

• r je absolutní hodnota (modul) komplexního čísla

• θ je argument komplexního čísla (úhel s kladnou reálnou osou)

Definuj Eulerův vzorec.

Eulerův vzorec říká, že pro každé reálné číslo x platí, že e^ix = cos(x) + i sin(x).To je základní vztah mezi exponenciální funkcí a trigonometrickými funkcemi.

Vysvětli, proč platí Eulerův vzorec.

Mějme Taylorův polynom pro e^ix. V tomto polynomu se střídají členy reálných a imaginárních částí. Pokud u imaginárních částí vytkneme i a současně seskupíme reálné části, dostaneme odhad cosx a sinx, pokud bychom s počtem členů (n) šli k nekonečnu. Tímto způsobem lze ukázat, že exponenciální funkce lze vyjádřit jako kombinaci trigonometrických funkcí.

Jaký je alternativní zápis komplexního čísla v geometrickém tvaru s využitím Eulerova vzorce?

z = re^iθ

Co to je de Moivreova věta?

Pro komplexní číslo z = r(cos θ + i sin θ) a přirozené číslo n platí z n = r n (cos(nθ) + i sin(nθ))

Jaké jsou výhody geometrického tvaru?

• snadná vizualizace komplexních čísel v komplexní rovině

• zjednodušení násobení a umocňování komplexních čísel

• přímá souvislost s goniometrickými funkcemi

Jaký má význam násobení komplexního čísla komplexní jednotkou?

Způsobuje rotaci bodu reprezentujícího komplexní číslo kolem počátku komplexní roviny o úhel ϕ.

Mějme komplexní číslo z = r(cos ϕ + i sin ϕ) = re^iϕ. Při násobení z komplexní jednotkou u dostaneme uz = (cos θ + i sin θ)(r cos ϕ + ir sin ϕ) = r(cos θ cos ϕ − sin θ sin ϕ) + ir(sin θ cos ϕ + cos θ sin ϕ) = r[cos(θ + ϕ) + i sin(θ + ϕ)] = re^i(θ+ϕ)

Co je to komplexní jednotka?

Komplexní jednotka je komplexní číslo s absolutní hodnotou 1. V polárním tvaru ji můžeme zapsat jako u = cos θ + i sin θ = e iθ kde θ je libovolný reálný úhel.

Jaký je geometrický význam násobení i?

Otočení o 90° proti směru hodinových ručiček.

Jaký je geometrický význam násobení -1?

Otočení o 180° proti směru hodinových ručiček.

Jaký je geometrický význam násobení -i?

Otočení o 270° proti směru hodinových ručiček.

Co platí pro význačné prvky tělesa?

Pro sčítání to je 0 a pro násobení to je 1. Musí být různé.

Definuj opačný prvek.

Prvek b ∈ K takový, že a + b = 0, je k danému a ∈ K určený jednoznačně. Tento jednoznačně určený prvek k danému a označujeme −a a nazýváme opačný prvek k a.

Definuj inverzní prvek/převrácenou hodnotu.

Prvek b ∈ K takový, že a · b = 1 je k danému 0 =/= a ∈ K určený jednoznačně – označujeme ho a⁻¹ nebo 1/a.

Jaké jsou vlastnosti těles?

Bud’ K těleso. Potom pro všechna n ∈ N a a, b, c, b1, . . . , bn ∈ K platí

• a + b = a + c ⇒ b = c,

• (a · b = a · c & a =/= 0) ⇒ b = c

• a · 0 = 0

• a · b = 0 ⇒ (a = 0 ∨ b = 0)

• −a = (−1) · a

• a · (b − c) = a · b − a · c

• a · (b1 + . . . + bn) = a · b1 + . . . + a · bn.

Co jsou to zákony o krácení?

Bud’ K těleso. Potom pro všechna n ∈ N a a, b, c, b1, . . . , bn ∈ K platí

• a + b = a + c ⇒ b = c,

• (a · b = a · c & a =/= 0) ⇒ b = c

Vysvětli, jak je možné zavést libovolné celočíselné násobky prvků z tělesa.

Pro a ∈ K, n ∈ N klademe (−n)a = −(na) = n(−a).

Vysvětli, jak je možné zavést libovolné celočíselné mocniny.

Podobně lze pro nenulové prvky tělesa zavést i libovolné celočíselné mocniny. Pro 0 =/= a ∈ K, n ∈ N klademe a −n = (a n ) −1 = (a −1 ) n .

Definuj podtěleso.

Podtěleso tělesa K je jeho podmnožina L, která obsahuje nulu a jedničku a je uzavřená vzhledem ke sčítání, násobení, opačnému a inverznímu prvku.

Nechť K je těleso a L ⊆ K. Říkáme, že L je podtěleso tělesa K, pokud 0, 1 ∈ L a pro všechna a, b ∈ L platí a + b ∈ L, ab ∈ L, −a ∈ L a, pokud a =/= 0, tak i a⁻¹ ∈ L.

Vysvětli pojem charakteristika tělesa.

Jedná se o nejmenší kladné celé číslo n takové, že n1 = 0.

Čemu může být rovna charakteristika tělesa?

∞ nebo prvočíslu

Co platí pro charakteristiku tělesa a jeho podtělesa?

charK = charL

Kdy má těleso charK = ∞ ? Uveď příklad takového tělesa.

Pokud neexistuje takové n, pro které platí n1 = 0, tedy pro každé celé n > 0 platí, že n1 =/= 0. Příklad: N, R, Q, …

Definuj konečná tělesa.

Jedná se o taková tělesa, jejichž charK =/= ∞.

Jaký význam mají konečná tělesa?

V kódování a kryptografii.

Definuj množinu zbytkových tříd modulo n.

Pro každé kladné celé číslo n označme Z_n = {k ∈ N | k < n} = {0, 1, . . . , n − 1}. Na této množine zavedeme dvě binární operace – sčítání ⊕ a násobení ⊙, které jsou odlišné od příslušných operací + a · v Z. Pro a, b ∈ Z_n klademe

• a ⊕ b = zbytek po dělení a + b číslem n

• a ⊙ b = zbytek po dělení a · b číslem n.

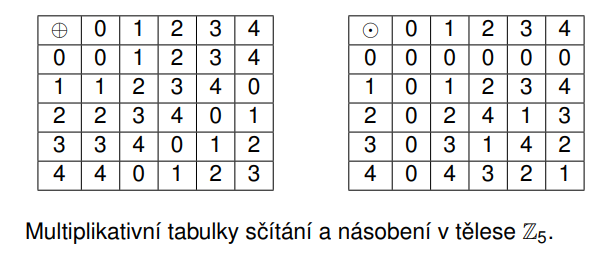
Kdy je množina Z_n těleso?

Množina Z_n s operacemi ⊕ a ⊙ je těleso právě tehdy, když n je prvočíslo.

Co znamená, že komplexní čísla s operacemi + a i tvoří těleso, které je algebraicky uzavřené?

Každá polynomiální rovnice s komplexními koeficienty má alespoň jedno komplexní řešení.

Definuj matici.

Necht’ X je libovolná množina a m, n ∈ N. Maticí typu m × n, nebo též m × n-rozměrnou maticí nad množinou X rozumíme obdélníkovou tabulku A = (a_ij)_m×n nebo A = (a_ij) (nebo viz foto), sestávající z prvků množiny X.

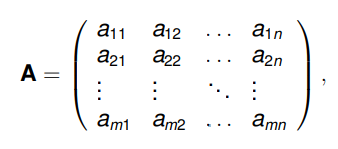
Co znamená a_ij v kontextu matic?

Jedná se o prvek matice, přičemž 1 <= i <= m a 1 <= j <= n. Jedná se tedy o prvek na i-tém řádku v j-tém sloupci.

Definuj totožné matice.

Jedná se o matice o stejných rozměrech, které mají na příslušných místech shodné prvky.

Definuj prázdnou matici.

Jedná se o matici o rozměru m x n, kdy m nebo n je rovno nule. V takovém případě se množina X^mxn sestává z jediné (prázdné) matice ∅.

Definuj transponovanou matici.

Jedná se o matici, kterou získáme záměnou řádků za sloupce. Je to matice A^T ∈ X^n×m, kde prvek na pozici (i,j) se stává prvkem na pozici (j,i).

Jaký je vztah mezi transponovanou maticí a zápisem pomocí řádků/sloupců?

Pro libovolnou matici A ∈ X^m×n a 1 ≤ i ≤ m, 1 ≤ j ≤ n platí s_i(A^T ) = r_i (A)^T , r_j(A^T) = s_j(A)^T_.

Definuj symetrickou matici.

Jedná se o takovou matici, jejíž transpozicí získáme totožnou matici.

Definuj diagonálu čtvercové matice.

Jedná se o posloupnost prvků (a₁₁, a₂₂, . . . , a_nn)-

Definuj blokovou matici.

Výsledná matice typu m × (n1 + n2 ) získaná spojením dvou matic. Značíme ji (A, B) nebo (A | B). Podobně lze postupovat u matice se stejným počtem sloupců. Všeobecným zápisem tak můžeme dostat větší systémy matic zapsané ve tvaru: A = (A_ij)_k×l, přicemž jednotlivé bloky A_ij jsou matice nad X rozměrů mi × nj , kde (m₁, . . . , m_k ), (n₁, . . . , n_l) jsou nejaké konečné posloupnosti přirozených čísel.

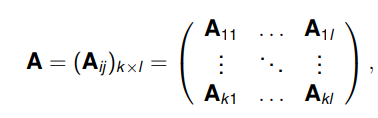
Definuj součet matic.

Pro matice A = (aij)_m×n, B = (bij)_m×n nad K platí

• A + B = (a_ij + b_ij)_m×n

Definuj násobení matice skalárem.

Pro matice A = (aij)_m×n, B = (bij)_m×n nad K a c ∈ K platí

• cA = (ca_ij)_m×n

Definuj neutrální prvek operace sčítání nad K^mxn

Nulová matice, tedy matice typu m × n, jejíž všechny prvky jsou nulové. Označujeme ji 0_m,n.

Definuj opačný prvek k matici A

−A = (−a_ij)_m×n

Definuj násobení vektorů.

Pro vektory u = (u1, u2, ..., un) a v = (v1, v2, ..., vn) nad K platí, že násobení vektorů může být definováno jako skalární součin, který je dán vzorcem u • v = u1v1 + u2v2 + ... + unvn.

Jaké jsou vlastnosti násobení dvou vektorů?

Pro všechna n ∈ N, c ∈ K a x, x′ ∈ K^1×n , y, y′ ∈ K^n×1 platí

• x · (y + y ′ ) = x · y + x · y ′ ,

• (x + x ′ ) · y = x · y + x ′ · y,

• x · cy = c(x · y) = cx · y,

• x · y = y^T · x^T

Definuj součin matic.

Nechť m, n, p ∈ N a A = (a_ij)_m×n, B = (b_jk)_n×p. Součinem matic A, B rozumíme matici

• A · B = (r_i (A) · s_k (B))_m×p = viz obrázek

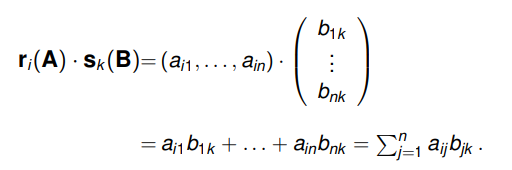
Vysvětli základní Leslieho populační model.

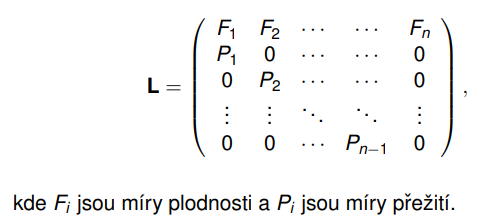
Leslieho model je diskrétní model, který se využívá k predikci velikosti a struktury populace na základě současných demografických údajů. Využívá matici přechodu, která popisuje, jak se populace mění v čase. Platí pro něj:

• obsahuje míru přežití a plodnosti pro každou věkovou skupinu

• populace jsou rozdělené do diskrétních věkových skupin

• předpoklad, že míra přežití a plodnosti je v čase konstantní

Jaká je základní rovnice Leslieho modelu?

n(t + 1) = L · n(t)

• n(t) je vektor populačních velikostí v čase t,

• L je Leslieho matice,

• n(t + 1) je vektor populačních velikostí v čase t + 1

Jaký tvar má Leslieho matice L?

Jaká jsou omezení Leslieho modelu?

• předpoklad konstantní míry přežití a plodnosti

• nebere v úvahu environmentální variabilitu

• ignoruje hustotní závislost a mezidruhové interakce

• může být nepřesný pro malé populace kvůli demografické stochasticitě

Jaké jsou vlastnosti násobení matic?

• distributivita

• asociativita

• násobení matic komutuje (je zaměnitelné s operací skalárního násobku)

Definuj jednotkovou matici řádu n.

I_n = (δ_ij)_n×n

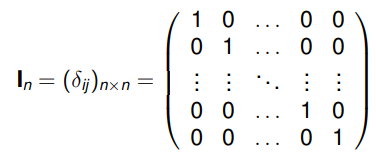
Jakou roli hraji jednotkové matice?

Role neutrálního prvku násobení.

Definuj mocniny čtvercových matic.

Pro A ∈ K^n×n , klademe A⁰ = I_n a A^k = A · . . . · A (k-krát) pro 0 < k ∈ N

Vysvětli obecně Markovův proces.

Jedná se o stochastický proces, který splňuje Markovovu vlastnost, tedy že budoucí stav závisí pouze na současném stavu, nikoliv na historii stavů.

Formuluj rovnici pro Markovův proces s diskrétním časem a konečným stavovým prostorem.

Nechť (X_t ) t∈T je Markovův proces s diskrétním časem a konečným stavovým prostorem S = {s1, s2, . . . , sn}. Lineární model pro tento proces je dán p(t + 1) = Pp(t), kde:

• p(t) = (p1(t), p2(t), . . . , pn(t))^T je vektor pravděpodobností stavů v čase t,

• P = (p_ij) je matice přechodových pravděpodobností.

Jak vypadá matice přechodových pravděpodobností?

p_ij reprezentuje pravděpodobnost přechodu ze stavu s_j do stavu s_i, přičemž platí, že součet pravděpodobností ve sloupci musí být roven 0.

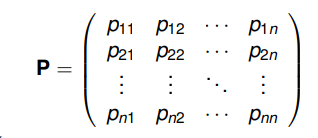
Co je to ergodický Markovův řetězec? Uveď příklad.

Speciální typ Markovova řetězce, kde se systém v dlouhodobém horizontu dostane do jakéhosi rovnovážného stavu, a to nezávisle na svém výchozím stavu. Příkladem může být házení kostkou.

Co platí pro ergodický Markovův řetězec? (matematicky)

Kde se Markovův proces využívá?

• analýza finančních trhů

• modelování biologických systémů

• simulace různých systémů

• zpracování přirozeného jazyka

• predikce počasí

• algoritmus pro simulaci a strojové učení

Definuj inverzní matici.

Inverzní matice existují pouze ke čtvercových maticím. Taková libovolná čtvercová matice A ∈ K^n×n bude mít nanejvýš jednu inverzní matici B ∈ K^n×n tak, že platí A · B = I_n = B · A

Jaké jsou vlastnosti inverzní matice?

Necht’ A, B ∈ K^n×n jsou regulární matice. Potom i matice A⁻¹ , A · B a A^T jsou regulární a platí:

• (A⁻¹)⁻¹ = A,

• (A · B)⁻¹ = B⁻¹ · A⁻¹ ,

• (A^T)⁻¹ = (A⁻¹)^T

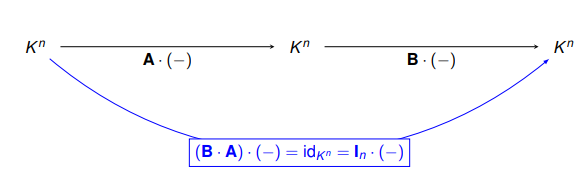
Definuj singulární a regulární matici.

Čtvercová matice A ∈ K^n×n je regulární, pokud k ní existuje inverzní matice A^-1. Pokud taková matice neexistuje, mluvíme o singulární matici.

Definuj ERO.

Necht’ A ∈ K^m×n . Necht’ matice B ∈ K^m×n vznikne z A provedením jedné ERO. Označme E matici, která vznikne z matice I_m provedením stejné ERO. Potom B = E · A.

Definuj ESO.

Necht’ A ∈ K^m×n . Necht’ matice C ∈ K^m×n vznikne z A provedením jedné ESO. Označme F matici, která vznikne z matice I_n provedením stejné ESO. Potom C = A· F.

Definuj elementární matici.

Jedná se o čtvercovou matici E ∈ K^n×n, které vzniknou z jednotkové matice I_n provedením jediné ERO nebo ESO.

Jaký je rozdíl mezi zleva elementární maticí a zprava elementární maticí?

zleva - vznikla provedením ERO

zprava - vznikla provedením ESO

Jak na výpočet inverzní matice pomocí ERO?

Necht’ A ∈ K^n×n a E₁, E₂, . . . , E_k ∈ K^n×n jsou elementární matice tak, že E_k · . . . · E₂ · E₁ · A = I_n. Potom A⁻¹ = E_k · . . . · E₂ · E₁.

Kdy jsou matice řádkově nebo sloupcově ekvivalentní?

Pro libovolné A, B ∈ K^m×n platí:

• A je řádkově ekvivalentní s B (A ∼ B) právě tehdy, když existuje regulární matice P ∈ K^m×m tak, že A = P · B;

• A je sloupcově ekvivalentní s B (A ≀ B) právě tehdy, když existuje regulární matice Q ∈ K^n×n tak, že A = B · Q.

Definuj LU-rozklad.

LU-rozklad matice A je faktorizace matice na součin dolní trojúhelníkové matice L (Lower) a horní trojúhelníkové matice U (Upper) tak, že platí A = LU, kde:

• A je čtvercová matice řádu n,

• L je dolní trojúhelníková matice s jednotkami na diagonále,

• U je horní trojúhelníková matice.

Jaké je využití LU rozkladu?

Strojové učení:

• Řešení soustav normálních rovnic v metodě nejmenších čtverců

• Výpočet inverzních matic v různých algoritmech

Grafické aplikace:

• Transformace souřadnic

• Řešení problémů souvisejících s geometrií

Inženýrství:

• Analýza konstrukcí

• Simulace proudění tekutin

Ekonomie:

• Ekonomické modelování

• Optimalizace portfolia

Jak zní věta o LU-rozkladu?

Nechť A je regulární matice rádu n, u které při Gaussově eliminaci nemusíme prohazovat řádky. Pak existují regulární matice L a U řádu n, pro které platí A = LU, L je dolní trojúhelníková matice s jednotkami na hlavní diagonále, U je horní trojúhelníková matice s nenulovými prvky na hlavní diagonále. Matice L a U jsou těmito podmínkami určené jednoznačně.

Jak lze řešit soustavu rovnic pomocí LU-rozkladu?

1. Provedení LU-rozkladu matice koeficientů

2. Řešení soustavy Ly = b pro y

3. Řešení soustavy Ux = y pro x

Kdy je užitečné řešit soustavu rovnic LU rozkladem?

Máme soustavu rovnic se stejnými koeficienty, ale s odlišnými pravými stranami.

Jaký je výpočet inverzní matice pomocí LU rozkladu?

1. LU rozklad matice A

2. Řešení soustavy pro každý sloupec jednotkové matice (musíme vyřešit AX = I, to znamená, že Ax_i = e_i, kde x_i je i-tý sloupec A^-1

3. Sestavení inverzní matice

Jaká je geometrická interpretace vektoru?

V prostoru vektory představujeme jako orientované úsečky (s počátečním a koncovým bodem).

Co je potřeba k tomu, aby byla úsečka umístěním nějakého vektoru?

Musí se jednat o stejný vektor, tedy musí být s původním vektorem rovnoběžná, stejně dlouhá a stejně orientovaná.

Jak sčítáme vektory?

Mějme dva vektory v rovině u = (u1, u2 ) ∈ R² , v = (v1, v2 ) ∈ R². Pro jejich součet platí u + v = (u1, u2 ) + (v1, v2 ) = (u1 + v1, u2 + v2 ). Geometricky se jedná o sčítání pomocí vektorového rovnoběžníku.

Jak násobíme vektory skalárem?

cu = c(u1, u2 ) = (cu1, cu2 ) pro c ∈ R, u = (u1, u2 ) ∈ R²

Definuj vlastnosti tělesa (matematickým zápisem).

• {0, 1} ∈ K, 0 ̸= 1

• operace ⊕, ⊙

• (∀a, b ∈ K)(a + b = b + a), (∀a, b ∈ K)(a · b = b · a), (komutativita)

• (∀a, b, c ∈ K)(a + (b + c) = (a + b) + c), (∀a, b, c ∈ K)(a · (b · c) = (a · b) · c), (asociativita)

• (∀a ∈ K)(0 + a = a), (neutrální prvek sčítání)

• (∀a ∈ K)(1 · a = a), (neutrální prvek násobení)

• (∀a ∈ K)(∃ b ∈ K)(a + b = 0), (opačný prvek)

• (∀a ∈ K ∖ {0})(∃ b ∈ K)(a · b = 1), (inverzní prvek)

• (∀a, b, c ∈ K)(a · (b + c) = (a · b) + (a · c)), (distributivita)

Definuj vektorový prostor.

Bud’ K (číselné) těleso. Vektorovým nebo též lineárním prostorem nad K nazýváme množinu V s význačným prvkem 0 a dvěma binárními operacemi – sčítáním +: V × V → V a násobením: K × V → V – takovými, že platí

• (∀x, y, z ∈ V)(x + (y + z) = (x + y) + z)), (asociativita sčítání)

• (∀x, y ∈ V)(x + y = y + x), (komutativita)

• (∀x ∈ V)(x + 0 = x), (neutrální prvek sčítání)

• (∀x ∈ V)(∃y ∈ V)(x + y = 0), (opačný vektor)

• (∀a, b ∈ K)(∀x ∈ V)(a · (b · x) = (ab) · x), (asociativita násobení skalárem)

• (∀x ∈ V)(1 · x = x),

• (∀a ∈ K)(∀x, y ∈ V)(a · (x + y) = (a · x) + (a · y)), (distributivita)

• (∀a, b ∈ K)(∀x ∈ V)((a + b) · x = (a · x) + (b · x)) (distributivita)

Jaký je rozdíl mezi axiómy vektorového prostoru a vlastnostmi (číselného) tělesa?

Násobení v číselném tělese K je binární operací na množině K (tj. zobrazení K x K → K). Násobení ve vektorovém prostoru V nad číselným tělesem K není binární operací na V, ale na K x V → V.

Definuj lineární kombinaci vektorů.

Lineární kombinace představuje postup, jak z určité množiny vektorů sestavit nový vektor jen pomocí sčítání a násobení. Mějme vektory x₁, x₂, …, x_n ∈ V, kde V je vektorový prostor a koeficienty a₁, …, a_n ∈ K. Lineární kombinací získáme vektor v = a₁×₁ + … + a_nx_n.

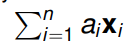
Definuj polynom nad tělesem.

Polynomem f stupně n, kde −1 ≤ n ∈ Z v proměnné x nad tělesem K rozumíme formální výraz tvaru f(x) = a₀ + a₁x + . . . + a_n−1x_n−1 + a_nx_n kde a0, a1, ..., an ∈ K jsou skaláry (koeficienty) polynomu f a an =/= 0.

Definuj lineární zobrazení.

Necht’ U, V jsou vektorové prostory nad tělesem K. Říkáme, že φ: V → U je lineární zobrazení, pokud φ zachovává operace vektorového součtu a skalárního násobku, tj. pokud pro libovolné x, y ∈ V, c ∈ K platí φ(x + y) = φ(x) + φ(y), φ(cx) = cφ(x)

Jaké jsou vlastnosti lineárního zobrazení?

φ: V → U a x ∈ V platí φ(0) = 0, φ(−x) = −φ(x)