MCR3U1 - Unit 1

State the parent function of a linear function

Pf: f(x) = x

Ff: f(x) = mx + b

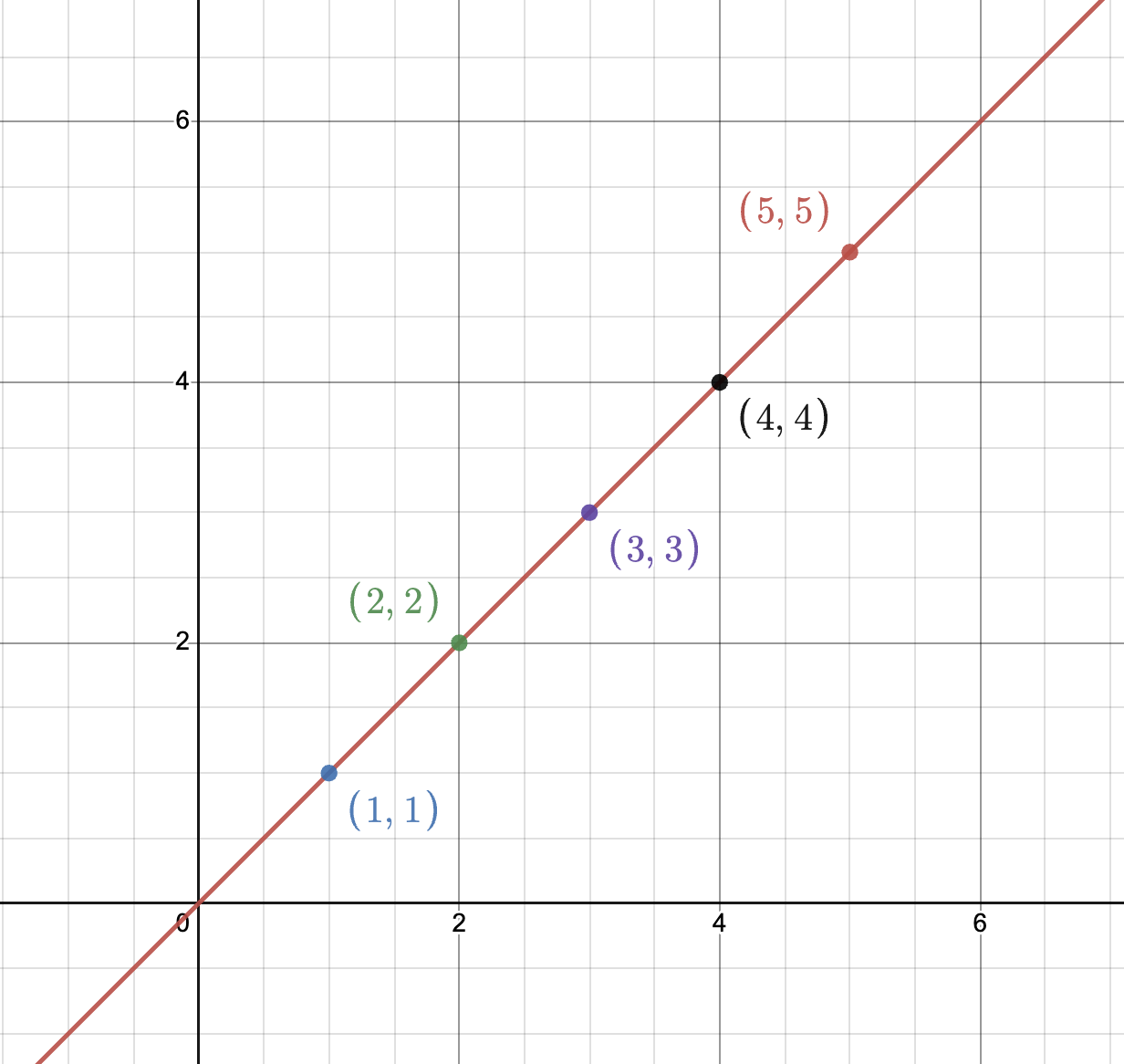
X	Y
1	1
2	2
3	3
4	4
5	5

Sketch out the parent function of a linear function. State the domain and range of the function

D: {XER}

R: {YER}

State the parent function of a Quadratic Function

Pf: f(x) = x²

Ff: f(x) = a(x-h)²+k

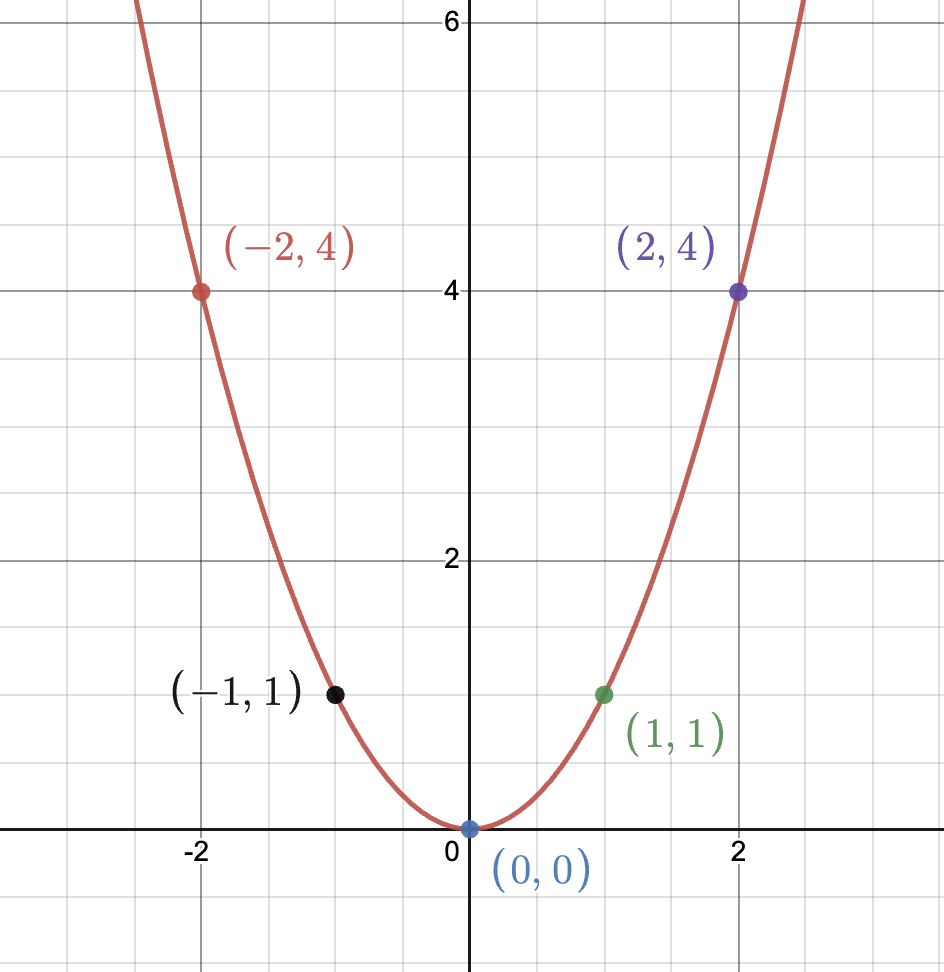
X	Y
-2	4
-1	1
0	0
1	1
2	4

Sketch out the parent function of a Quadratic Function. State the domain and range of the function

D: {XER}

R: {YER | y >= k} - (+a)

R: {YER | y <= k} - (-a)

State the parent function of a Absolute Value Function

Pf: f(x) = |x|

Ff: f(x) = a|k(x-d)| + c

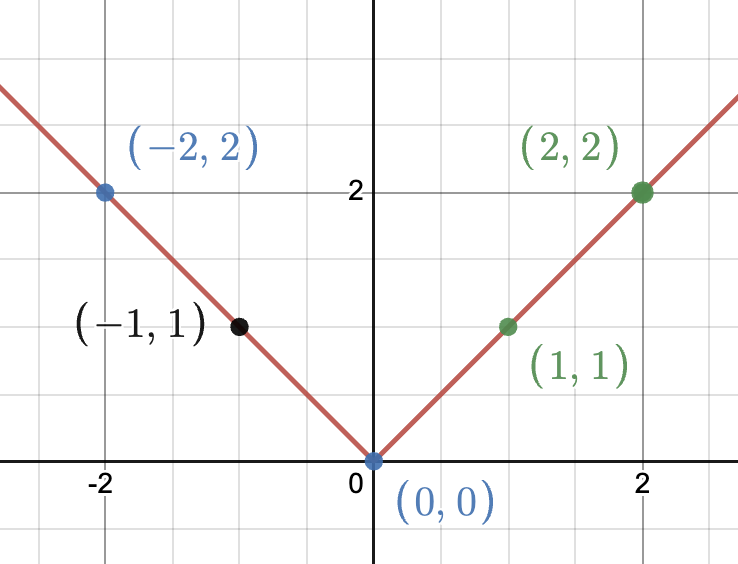
X	Y
-3	3
-2	2
-1	1
0	0
1	1
2	2
3	3

Sketch out the parent function of an Absolute Function. State the domain and range of the function

D: {XER}

R: {YER | y >= c} - (+a)

R: {YER | y <= c} - (-a)

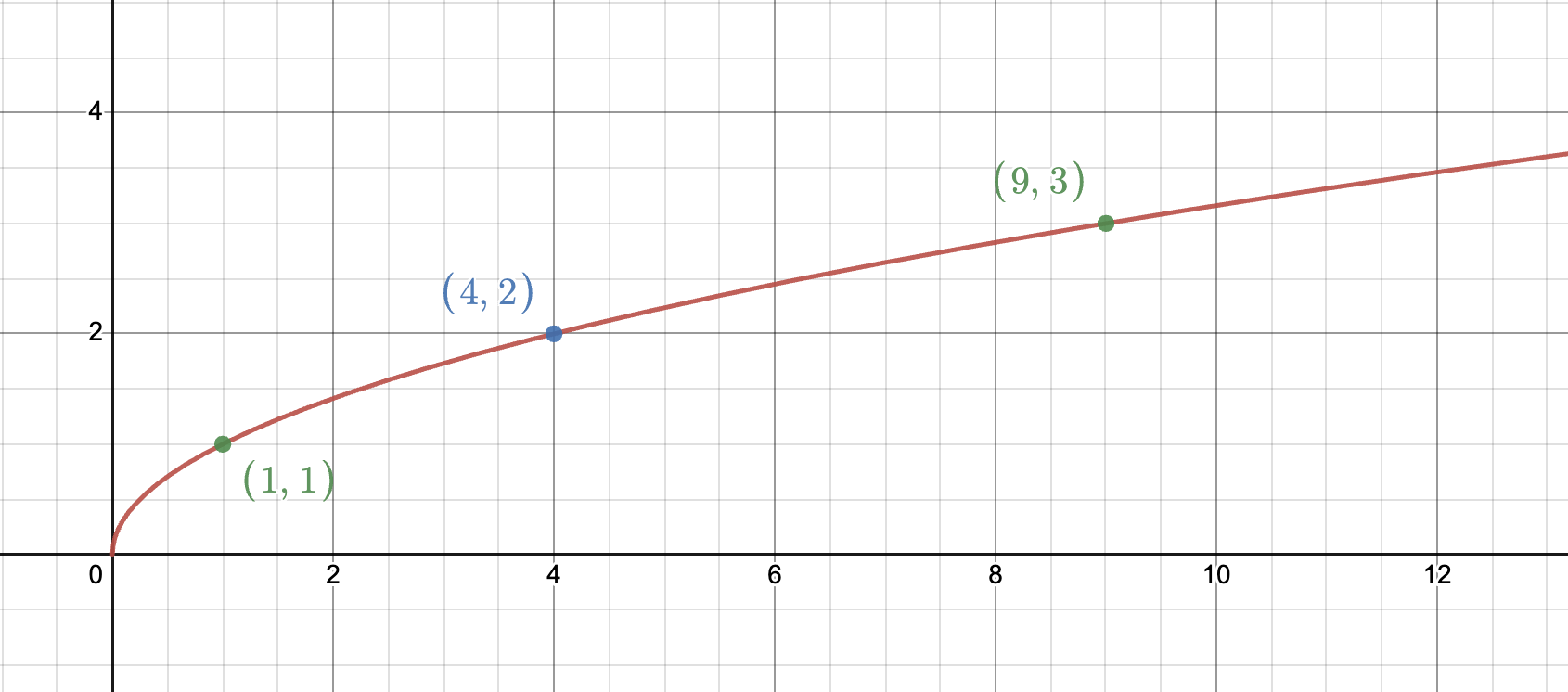
State the parent function of a Square Root Function

Pf: f(x) = √x

Ff: f(x) = a√k(x-d) + c

X	Y
0	0
1	1
4	2
9	3

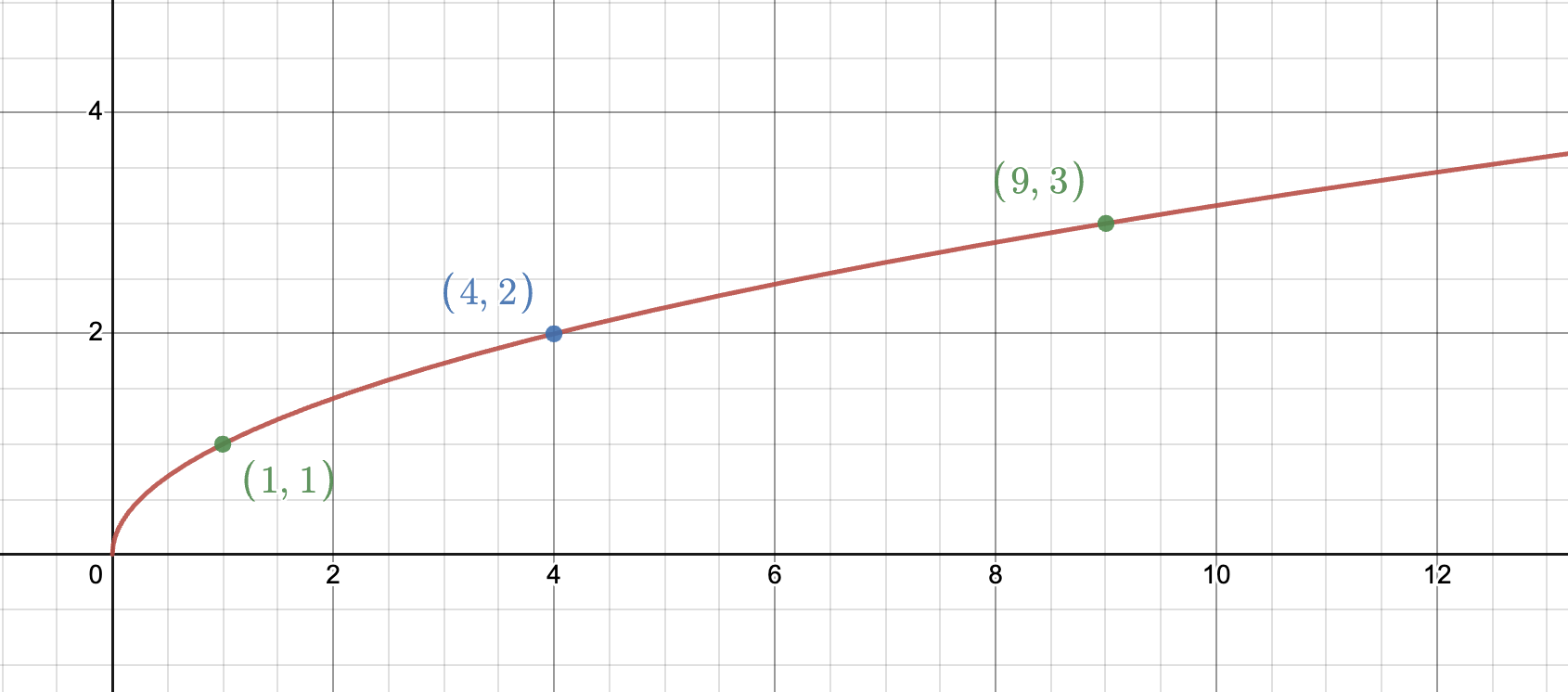
Sketch out the parent function of an Square Root Function. State the domain and range of the funciton

D: {XER | x >= d} if k is (+)

D: {XER | x <= d} if k is (-)

R: {YER | y >= c} if a is (+)

R: {YER | x <= c} if a is (-)

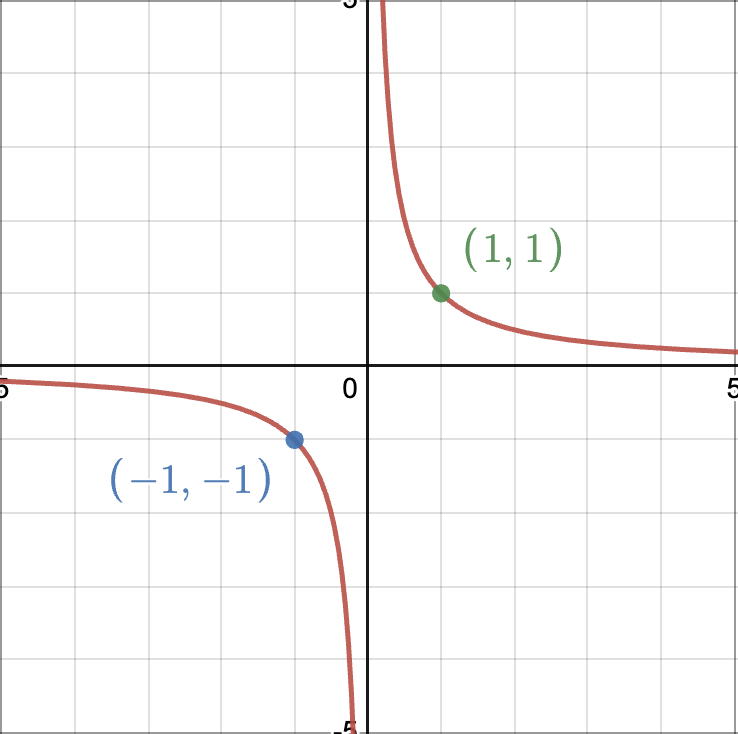
State the parent function of a reciprocal function

Pf: f(x) = 1/x

Ff: f(x) = a(k/x-d) + c

X	Y
1	1
-1	-1

Sketch the parent function of a Reciprocal Function. State the domain and range of the function

D: {XER | x ≠ d}

R: {YER | y ≠ c}

What are the restrictions for a square root function and a reciprocal function

Square Root Function:

• The value inside the square root cannot be less than 0

Reciprocal Function":

• The value in the denominator cannot equal 0

Vertical Compression

0 < a < 1

Vertical Expansion/Stretch

a > 1

Reflection off the x-axis

a = (-)

Horizontal Compression

k > 1 —> graph is horizontally compressed b.a.f.o k/1

Horizontal Expansion/Stretch

0 < k < 1—> graph is horizontally stretched b.a.f.o k/1

Describe the following function:

f(x) = -1[-2(x+5)²]-1/2

a = -1

k = -2

d = -5

c = -1/2

• Reflecting on the x and y axis

• Horizontally compressed by b.a.f.o of ½

• Horizontally translated 5 units to the left

• Vertically translated ½ or 0.5 units down