Normal Distributions and Bivariate Data

bivariate data

Data with two variables, or pairs of numerical observations.

Correlation

A measure of the extent to which two factors vary together, and thus of how well either factor predicts the other.

positive correlation

A correlation where as one variable increases, the other also increases, or as one decreases so does the other. Both variables move in the same direction.

negative correlation

One variable increases while the other decreases.

explanatory variable

A variable that helps explain or influences changes in a response variable (independent variable)

response variable

A variable that measures an outcome of a study (dependent variable)

correlation coefficient

a statistical index of the relationship between two things (from -1 to +1)

Strong r value

closer to 1 or -1

Weak r value

close to 0

coefficient of determination

r^2

What does the coefficient of determination tell you

The percent of the variability in y (response variable) that can be explained by x (the independent variable)

Correlation does NOT imply

causation

What signifies a prediction in a word problem?

A hat ^

Analysis of regression equation

Predicted response variable = slope (coefficient for explanatory variable) + constant

Residual

Margin of error

residual equation

observed y - predicted y

How to find observed y

Find point on scatter plot

How to find predicted y

Plug in x value into y=mx+b

Sum of residuals should always be

0

If a point is above the trend line

It has a positive residual AND the point has been underestimated

If a point is below the trend line

It has a negative residual AND the point has been overestimated

Three Types of Correlation relationships

Causal relationship, common response relationship, confounding relationship

Causal Relationship

Changing x CAUSES y to change. The only way to show causation is through a controlled designed experiment.

Common response relationship

Both x and y respond to changes in a third lurking variable.

Example of a common response relationship

Spelling ability rises as shoe size increases. The lurking variable here is age.

Confounding relationship

A confounded relationship occurs when we can't separate the effects of multiple explanatory (x) variables

Example of a confounding relationship

Someone has calf pain, and after some practices, the pain decreases. We cannot say what explanatory variable actually worked, because the person stretched, decreased running mileage, and bought new shoes.

What does the y intercept or "constant" represent in regression analysis

The predicted value of y when all x variables in the model are equal to 0

Hopelessly confounded variables

X variables that cannot be separated (in a confounding relationship)

What does the line of best fit do?

The line of best fit minimizes the sum of the squared residuals

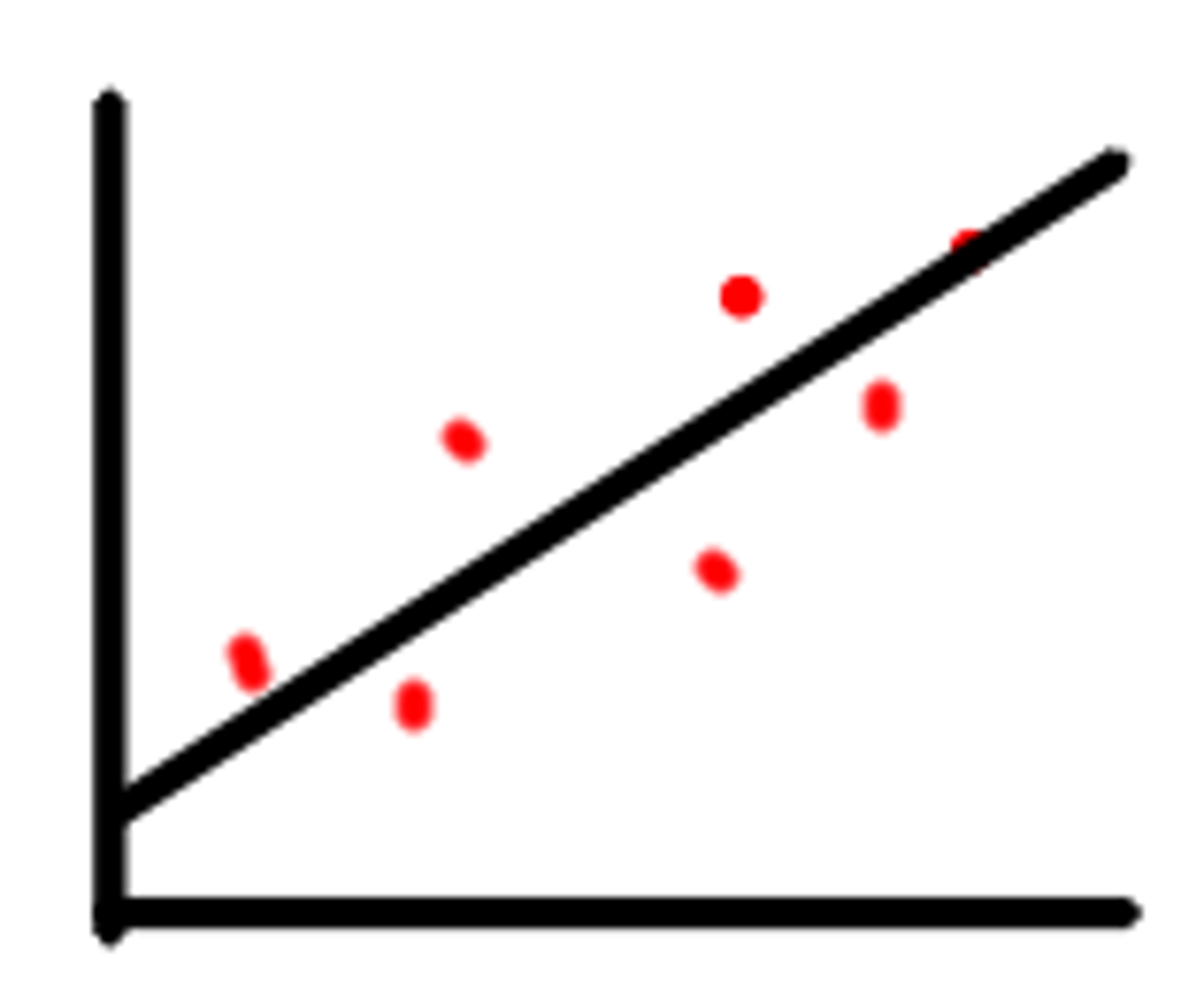
Least squares regression line

Line of best fit

influential observation

The most influential observations or points on a graph are points that are extreme in their x-value

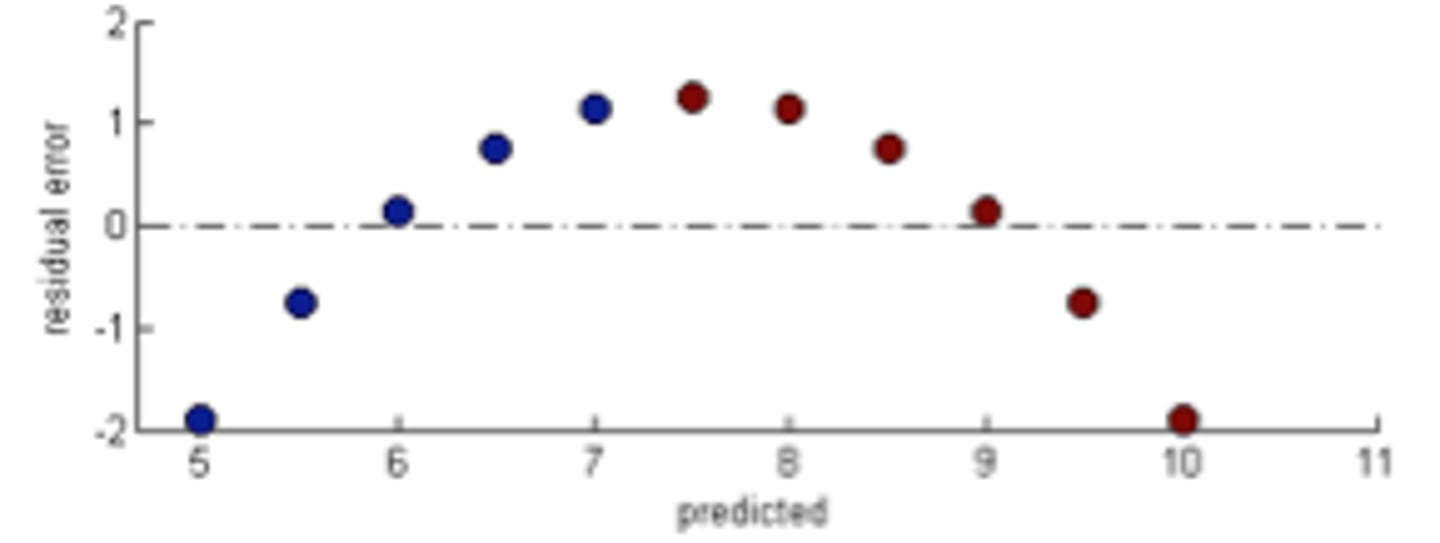
How to interpret a residual plot

For a residual plot, you always want small residuals, and they should be randomly scattered above and below the trendline

What does it mean if you see a pattern in your residual plot?

Another model is better

How to build a non-linear regression model

Transform the response variable using a mathmatical function, and then run a linear regression on the transformed data

Cubic regression model example

Take the cube root of the response (y) variables to shift data. Now your predicted y is the cube root of y instead of regular y. So, when predicting a specific point, make sure to cube both sides.

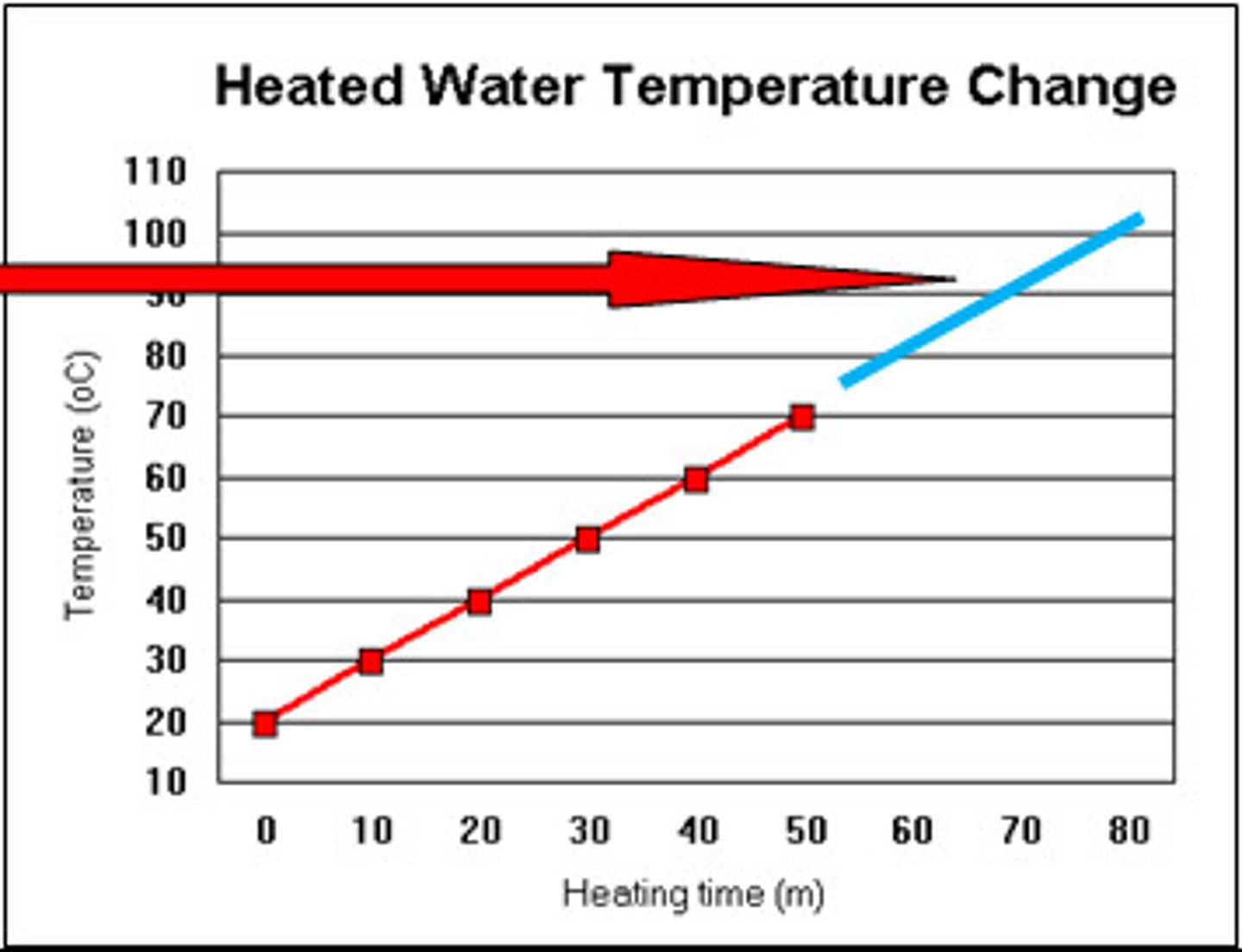
extrapolation

Estimating a value outside the range of measured data.

Can a r value go above 1 or below -1

No

How to find the slope with r

r (sy/sx)