Time Complexity and Algorithm Classifications

what is a selection sort?

Selection Sort algorithm repeatedly finds the smallest element in the unsorted tail region of a list and moves it to the front

what is the time complexity for a selection sort?

With an array of size n, count how many primitive operations are needed:
1st run = n + 2
2nd run = (n -1) elements + 2 operations
3rd run = (n-2) elements + 2 operations
2 is the swapping operations
minus 1 from n each time because biggest value at the end so doesn't need to be swapped

simplified to O(n²)

what is a search algorithm?

check for an element from any data structure where it is stored

what are the 2 main search algorithms?

sequential search
interval search

what is a sequential search + example?

eg. linear search
list traversed sequentially and every element checked
list does not need to be sorted
brute force algorithm

what is an interval search + example?

eg. binary search
divide and conquer algorithm
list must be sorted

what is the time complexity for binary search?

O(log₂n)

what is the time complexity for linear search?

O(n)

is binary search or linear search faster?

binary search

for an unsorted list of millions of elements, is binary or linear search better + why?

* binary search needs an already sorted array so combined with selection sort, time complicity = n² causing overall algorithm slower
* if performing search multiple times, use binary as we only have to sort once
* if performing search once, better to use linear

what is polynomial time?

an algorithm is solvable in polynomial time if the number of steps required to complete the algorithm for a given input is O(nᵏ) for some non-negative integer k, n being the complexity of the input

for algorithms with high computational complexity, how do we know there isn't a better algorithm with a lower time complexity?

we are dividing algorithms into classifications which limits the lowest time complexity it can have

what are the ways a problem can be classified

computable
non-computable

P problems
NP problems
NP-complete problems
NP-Hard problems

what is a computable problem?

problem can be solved using computer

what is a non computable problem?

can't be solved using computer
eg. halting problem

what are P problems?

* solved in polynomial time aka. a reasonable amount of time

what are examples of P problems?

eg. search and sort algorithms

what are NP-Complete problems?

The hardest problems in NP set

* No polynomial-time algorithm is discovered for any NP-complete problem
* Verifiable in polynomial time but time complexity is greater than polynomial time

what are examples of NP-complete problems?

travelling salesperson?

knapsack problem

finding shortest common superstring

Given three positive integers a, b, and c, do there exist positive integers (x and y) such that ax2 + by2 = c

what are NP problems?

* difficult to solve in polynomial time
* easy to verify the solution in polynomial time

\

what are examples of NP problems?

eg. network routing, database problems, scheduling

non-deterministic algorithms

decision-making problems

why are NP-Complete problems the intersection of P and NP problems?

Nobody was able to prove that no polynomial-time algorithm exist for any of the problems even though there currently aren't any

what are NP-Hard problems?

* Difficult to solve problems which cannot be solved in polynomial time
* difficult to verify in polynomial time

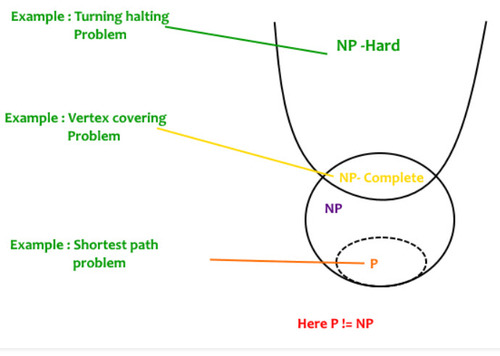
what is the main structure of algorithm classification?

P problems are a subset of NP problems
Non-computable problems are a subset of NP-Hard problems
NP-Complete problems are the intersection of NP and NP-Hard problems

what are the consequences if a polynomial time algorithm is found for any problem in the NP-Complete set?

every problem in NP can be solved in polynomial time
NP-Complete would no longer be in intersection and would be a proper subset of NP

what are the consequences if P problems are equal to NP problems?

all problems we have would be solvable in polynomial time
no security possible as any encryption could be decrypted in polynomial time