Lesson 5.3 Gravitational fields

What is a gravitational field?

The region of space surrounding a body in which another body experiences a force of gravitational attraction. The field mediates (brings about) the gravitational force between objects.

What is the difference between a scalar field and a vector field?

A scalar field has magnitude only at each point (e.g. temperature field). A vector field has both magnitude and direction at each point. Gravitational fields are vector fields because force has direction.

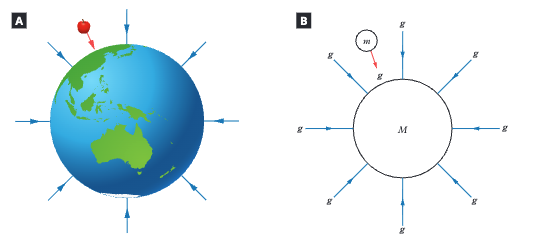
What is the direction of a gravitational field?

The direction of the net gravitational force at that point. For Earth this is toward Earth's centre (what we call "down"). Field lines point radially inward toward the centre of mass.

What is gravitational field strength and what are its two equivalent formulas?

Gravitational field strength (g) is the force per unit mass at a point in the field. Formulas: g = F/m (force per unit mass) and g = GM/r² (from Newton's law). Units: N kg⁻¹ or equivalently m s⁻².

Why does gravitational field strength not depend on the mass of the object in the field?

From g = F/m = (GMm/r²)/m the test mass m cancels giving g = GM/r². Field strength depends only on the mass M creating the field and distance r from its centre. A 1 kg and 100 kg object experience the same g at the same location.

How does gravitational field strength vary with altitude above Earth's surface?

g decreases with altitude following an inverse square relationship. At 2 Earth radii from centre (1 Earth radius above surface) g = 9.8/4 = 2.45 m s⁻². At 3 Earth radii from centre g = 9.8/9 = 1.09 m s⁻².

Why does g vary slightly at different locations on Earth's surface?

Earth's radius varies from equator (6.37 × 10⁶ m) to poles (6.36 × 10⁶ m). Since g = GM/r² smaller radius means larger g. At equator g ≈ 9.76 m s⁻² while at poles g ≈ 9.83 m s⁻². QCAA uses g = 9.8 m s⁻² as average.

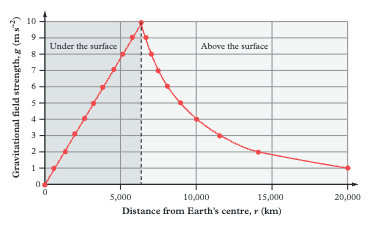
What happens to gravitational field strength inside the Earth?

At Earth's centre g = 0 because gravitational pulls from all directions cancel out. From centre to surface g increases linearly. Above the surface g decreases following the inverse square law.

What does "weightless" actually mean and why are astronauts not truly weightless?

Weight = mg so "weightless" would mean g = 0. Astronauts on the ISS still experience g (about 8.7 m s⁻² at that altitude). They feel weightless because they are in free-fall along with the station. Their weight is not zero - they are just falling.

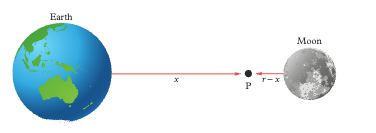
Where between Earth and Moon is the gravitational field strength zero and why?

At point P where gravitational pulls from Earth and Moon are equal and opposite. Since Earth is more massive P is closer to the Moon. Found by setting g_Earth = g_Moon: GM_Earth/x² = GM_Moon/(r-x)² and solving for x.

Calculate the gravitational field strength at a point 100000 km above Earth's centre. (M_Earth = 5.97 × 10²⁴ kg and r_Earth = 6.37 × 10⁶ m)

r = 100000 km = 1.0 × 10⁸ m. g = GM/r² = (6.67 × 10⁻¹¹ × 5.97 × 10²⁴)/(1.0 × 10⁸)² = 3.98 × 10¹⁴/1.0 × 10¹⁶ = 0.040 m s⁻² (2 s.f.). This is about 1/245 of surface gravity showing how rapidly g decreases with distance