Calculus Derivatives

Derivative of a Constant

0

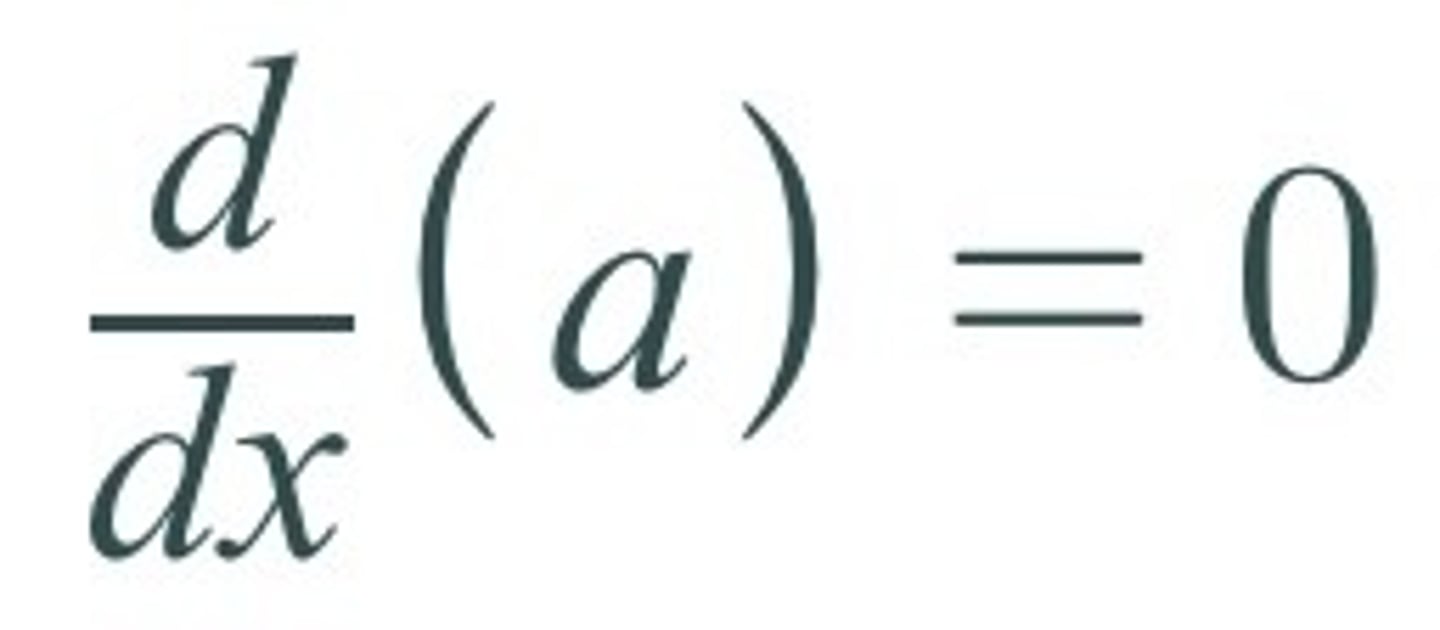
d/dx [ax] =

a

d/dx [√(x+-a)] =

1/2√(x+-a)

Power Rule: d/dx [xᵃ] =

a(xᵃ⁻¹)

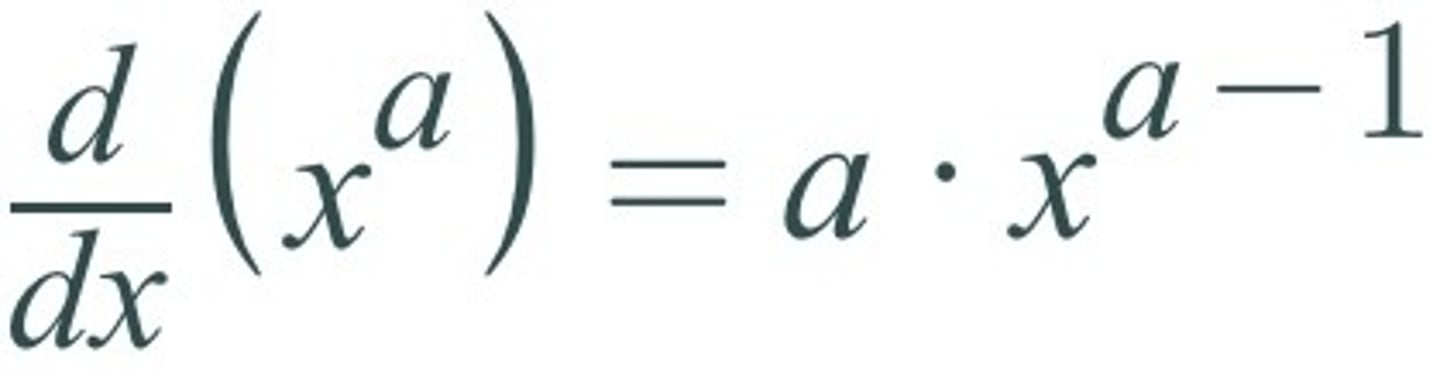
d/dx [eˣ] =

eˣ

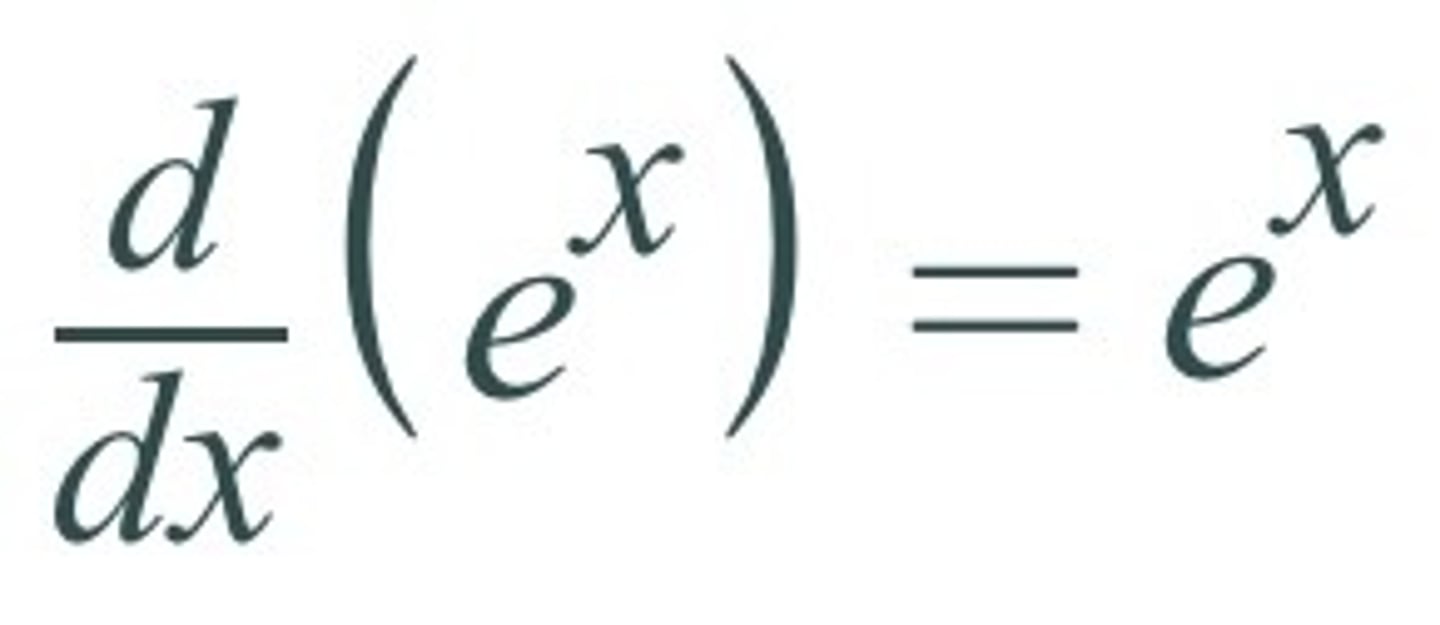
d/dx [eᵃˣ] =

a(eᵃˣ)

d/dx [ln(|x|)] =

1/x

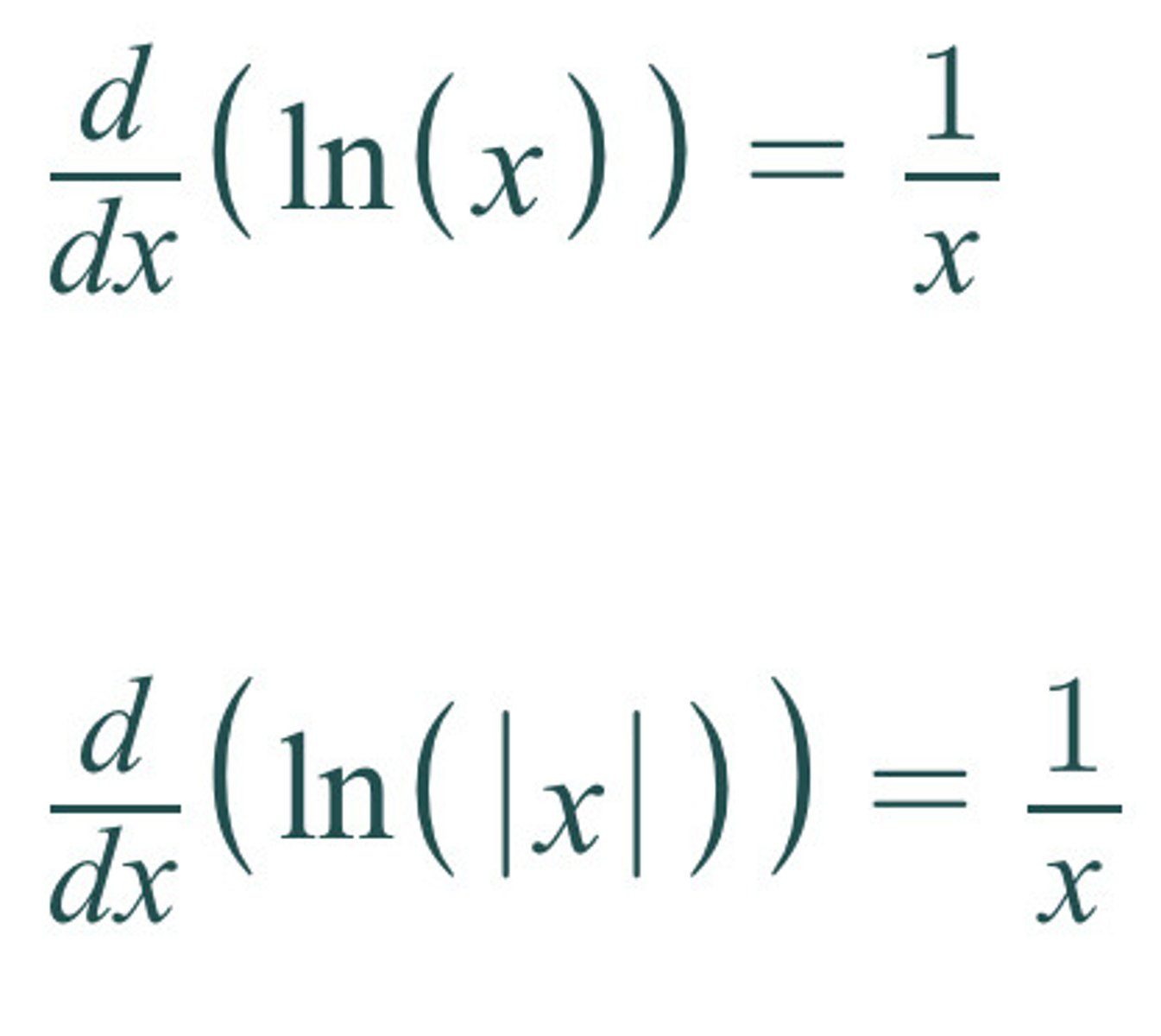
d/dx [aˣ] =

aˣ[ln(a)]

d/dx [sin(x)] =

cos(x)

d/dx [cos(x)] =

-sin(x)

d/dx [tan(x)] =

sec²(x) or (sec x)²

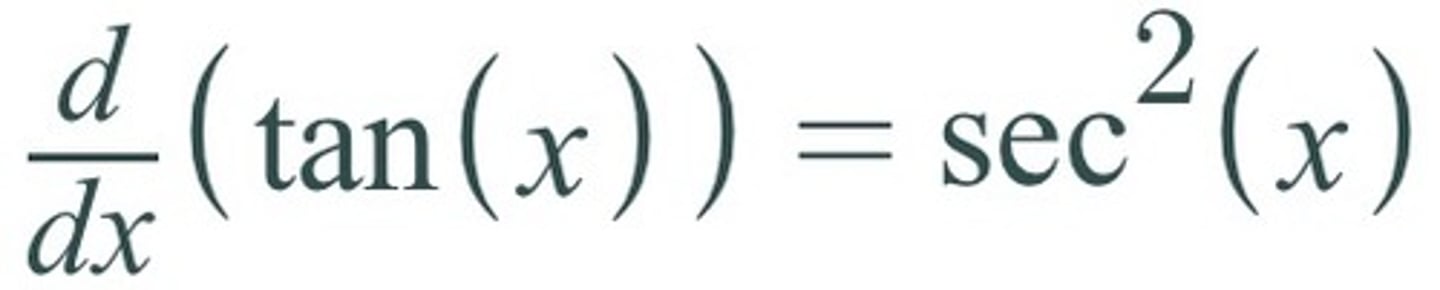
d/dx [cot(x)] =

-csc²(x) or -(csc x)²

d/dx [sec(x)] =

sec(x)tan(x)

d/dx [csc(x)] =

-csc(x)cot(x) or -cot(x)csc(x)

d/dx [arcsin(x)] =

1/√(1-x²)

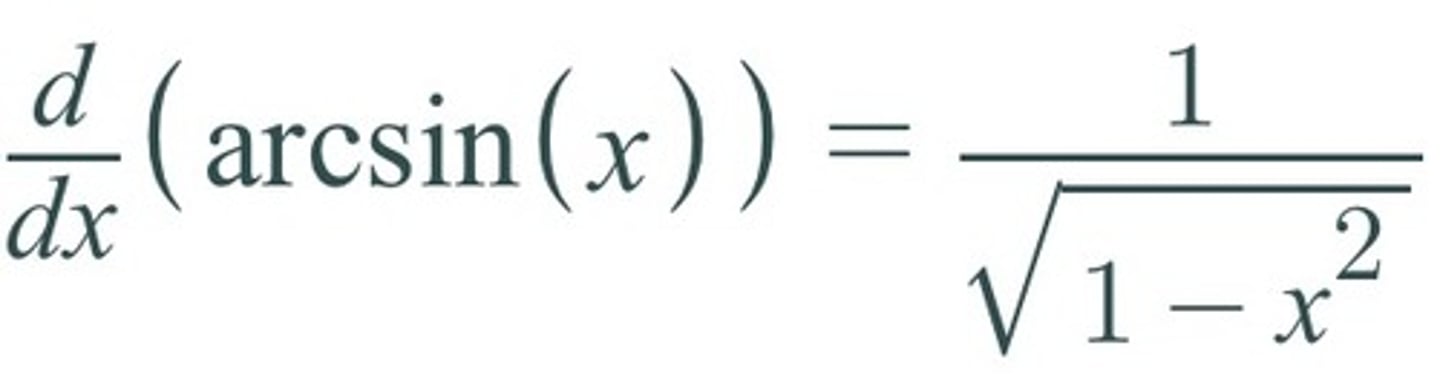
d/dx [arccos(x)] =

-1/√(1-x²)

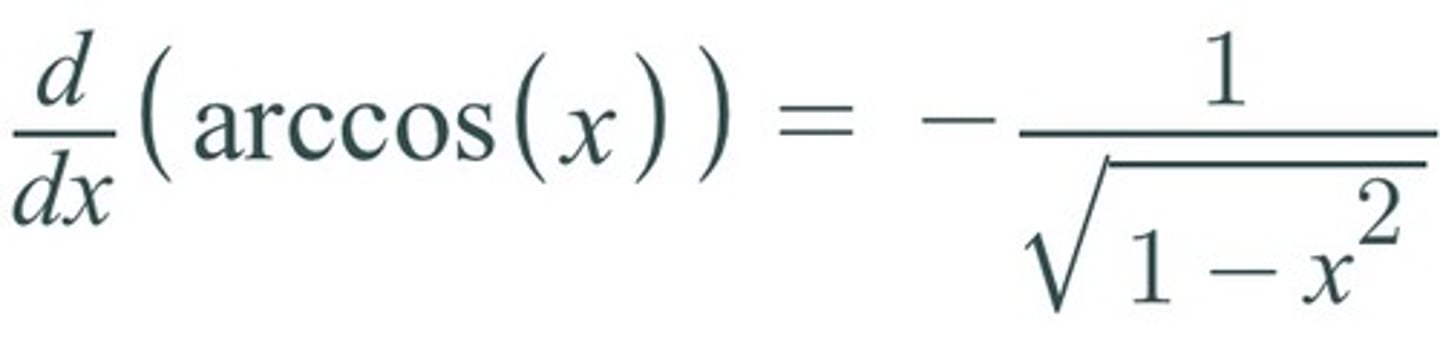
d/dx [arctan(x)] =

1/(1+x²)

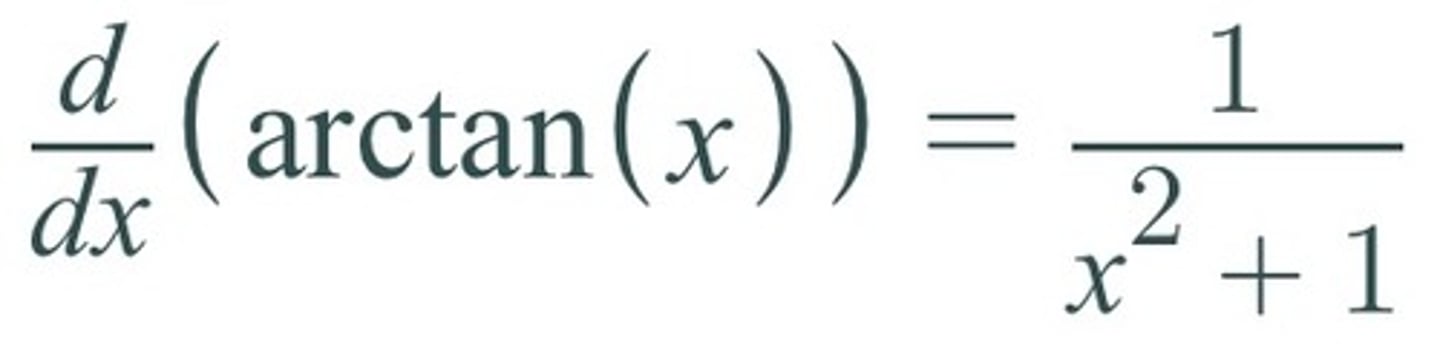
d/dx [arccot(x)] =

-1/(1+x²)

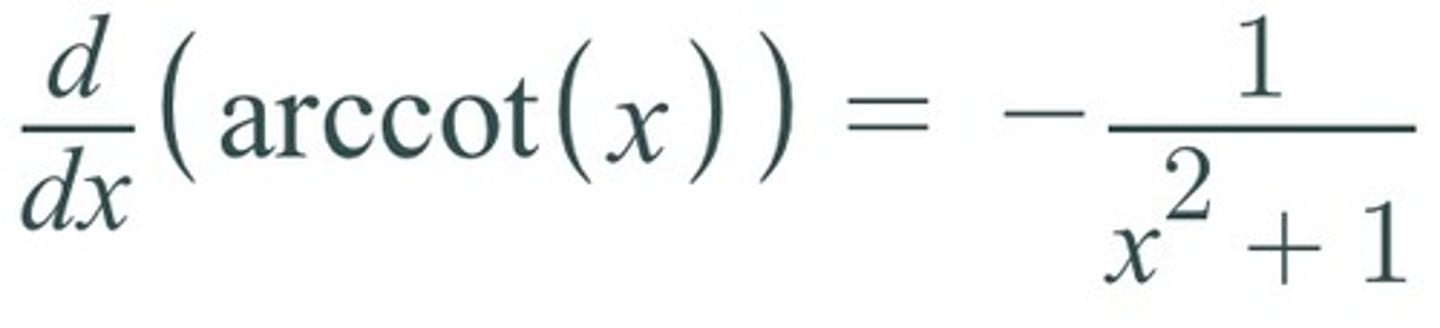
d/dx [arcsec(x)] =

1/x√(x²-1)

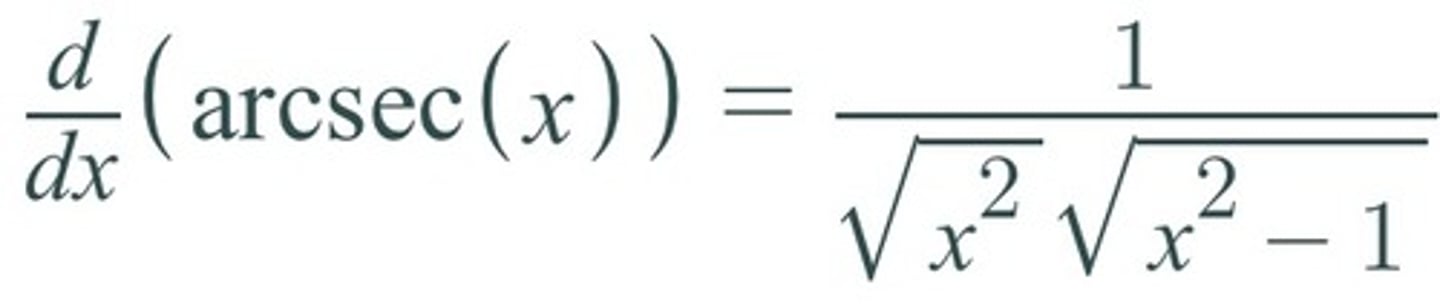
d/dx [arccsc(x)] =

-1/x√(x²-1)

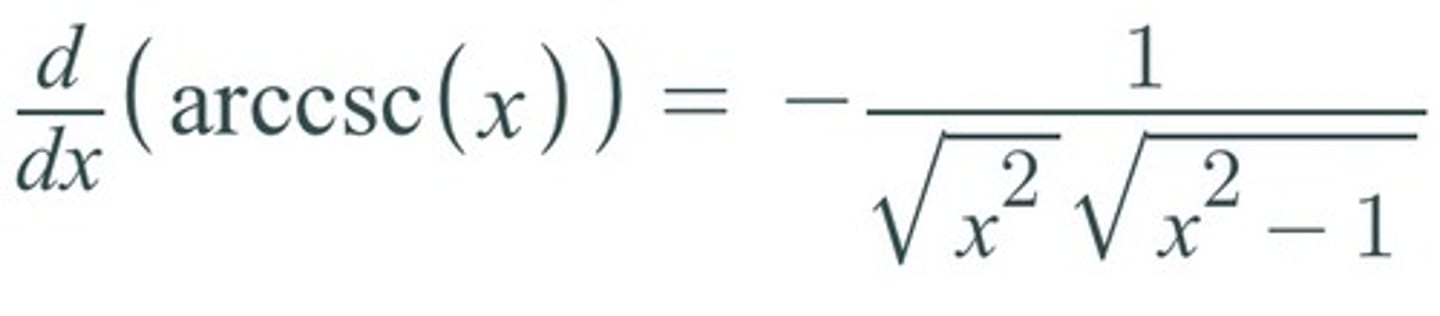
d/dx [logₐ(x)] =

1/xln(a)

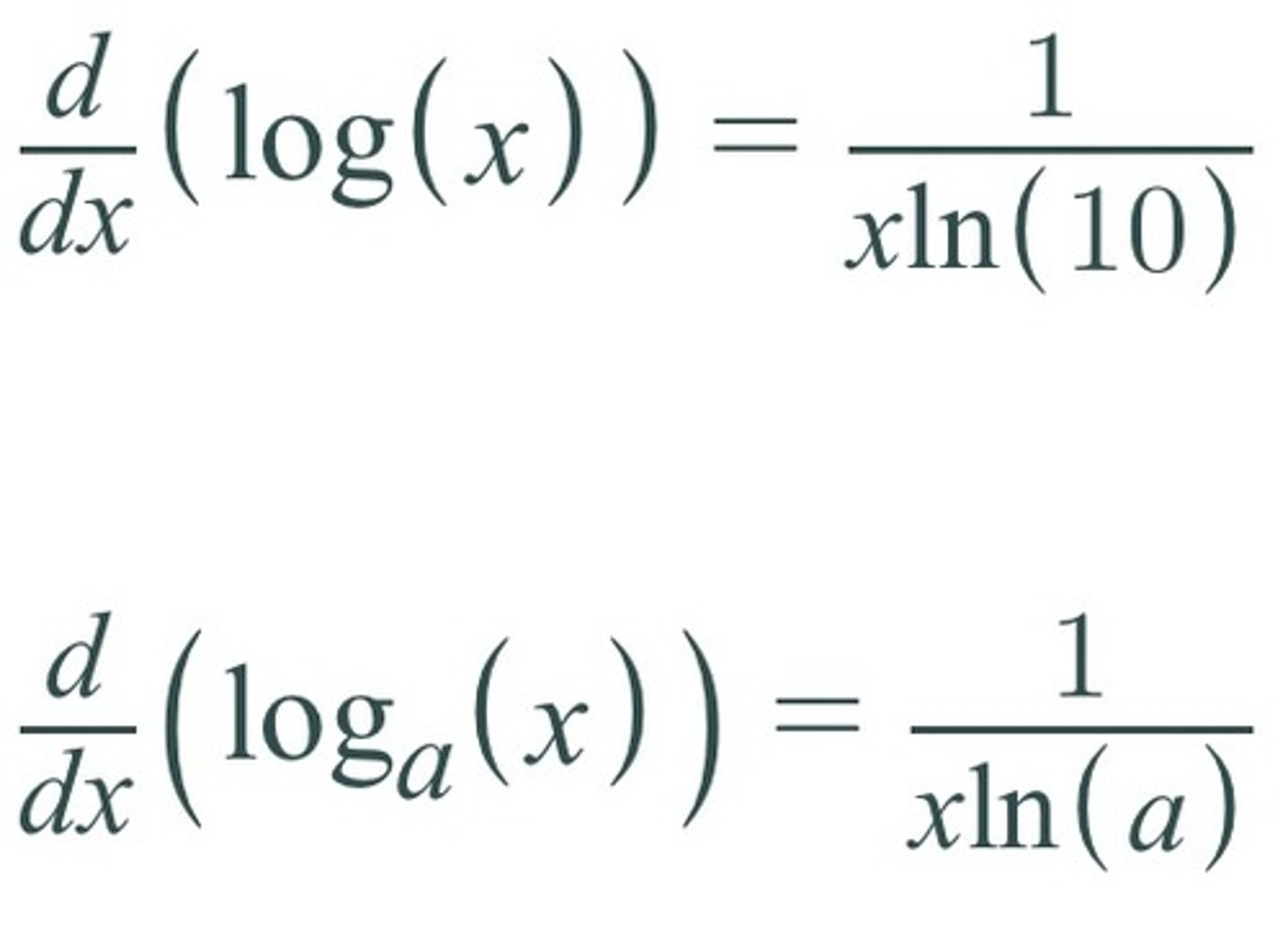
Sum-Difference Rule: d/dx [f(x) +- g(x)] =

f'(x) +- g'(x)

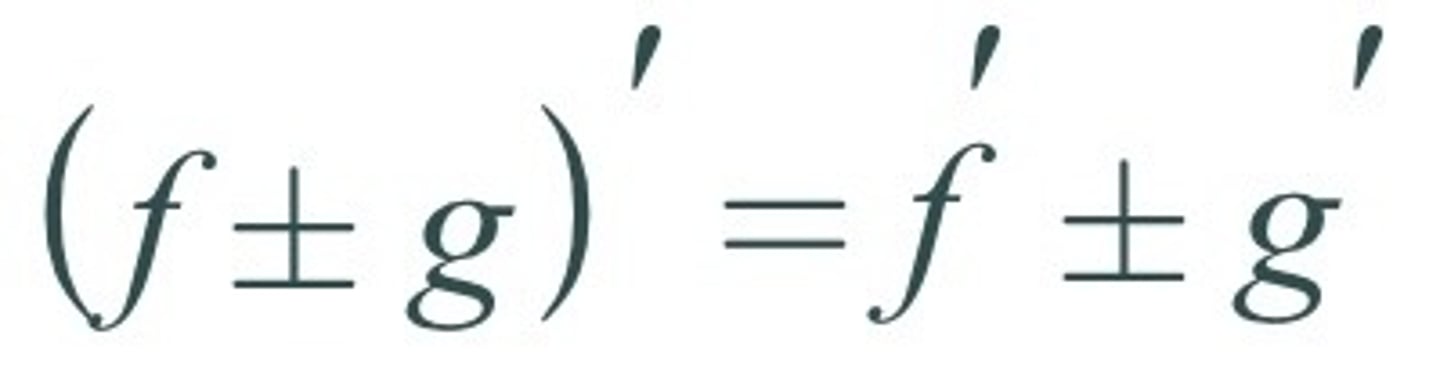
Constant Out Rule: d/dx [a • f(x)] =

a • f'(x)

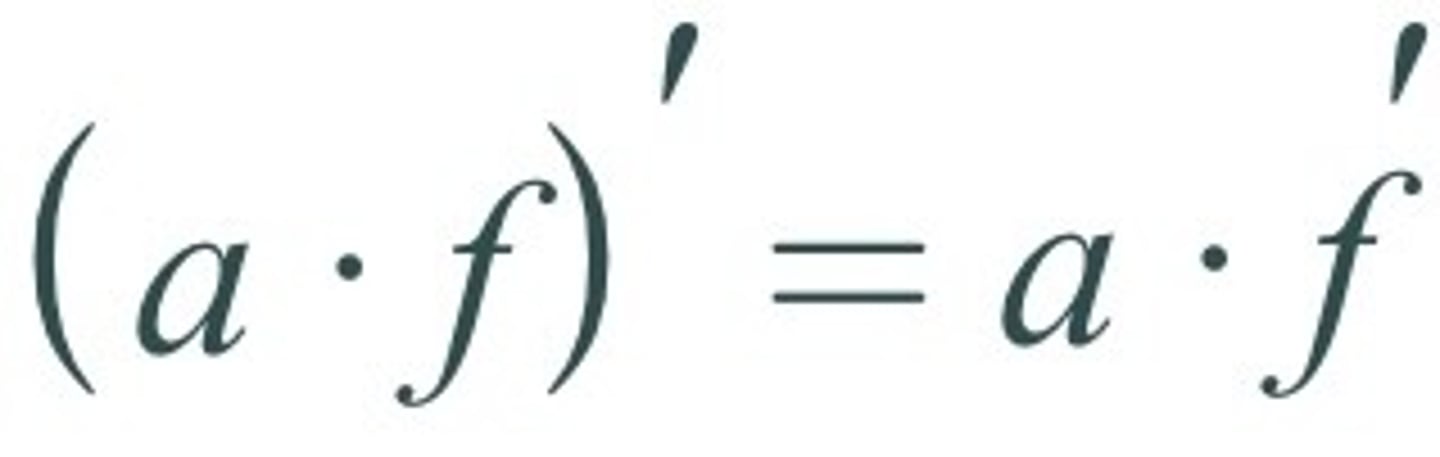
Product Rule: d/dx [f(x)g(x)] =

f'(x)g(x) + f(x)g'(x)

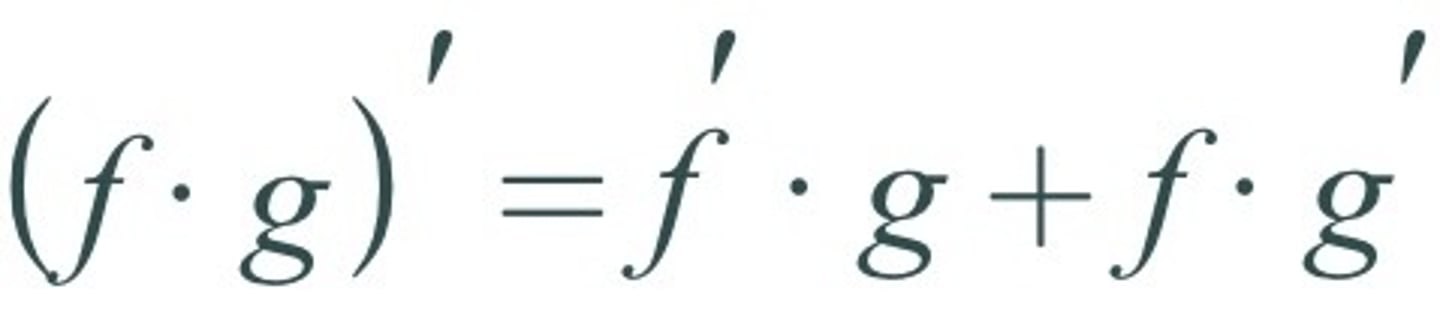
Quotient Rule: d/dx [f(x)/g(x)] =

[f'(x)g(x)-f(x)g'(x)]/[g(x)]²

Chain Rule: df(u)/dx =

df/du • du/dx

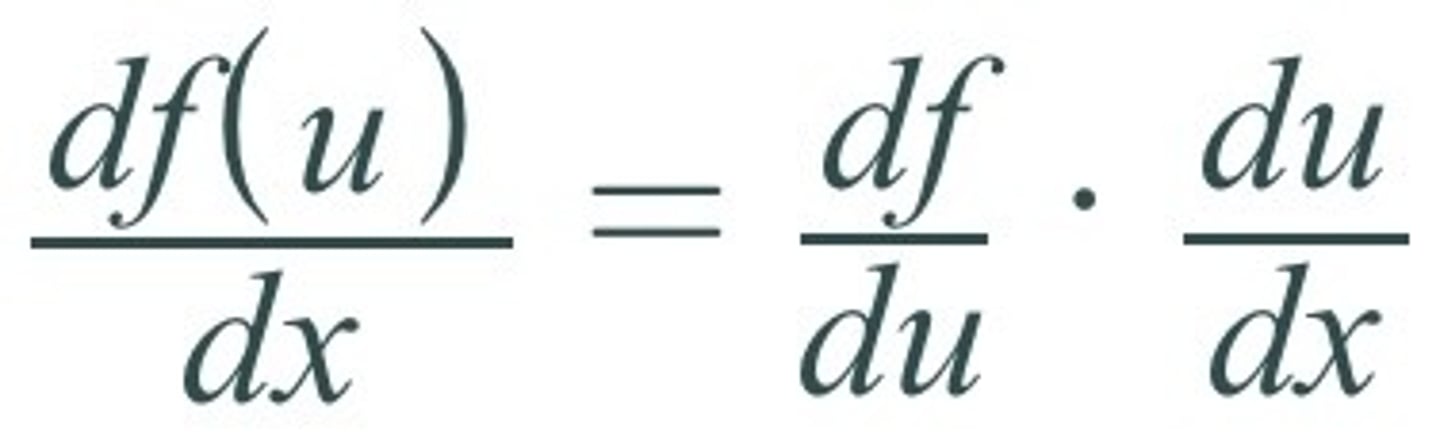
dx =

(1/u')du or x'du