Algorithms for Graphs - Week 7

What is a walk?

A sequence of vertices (𝑣₀, 𝑣₁, … , 𝑣_k
such that (𝑣_i, 𝑣_i+k) ∈ 𝐸. The length of the walk is k (the number of edges used).

How is a path different from a walk?

Forbids us returning to the same vertex again, (all vertices are distinct), so the edges and vertices are all different from one another.

What is a complete graph?

Where there is an edge between all pairs of vertices.

For n vertices, how many edges are there in a complete graph?

n(n-1)/2

How many walks are there for a sequence of vertices starting at u and ending at v?

Infinite

How many walks are there for a sequence of vertices starting at u, ending at v with length k+1?

Walks of length k: so n^k-1 number of walks

How many numbers of paths are there?

(n-2)!/(n-k-1)!

What do:

sp(𝑢, 𝑣) and l(sp(𝑢, 𝑣)) represent?

sp(𝑢, 𝑣) → The shortest path between u and v

l(sp(𝑢, 𝑣)) → The length of the path

If 𝑤 ∈ sp(𝑢, 𝑣) then what is sp(𝑢, 𝑣) equivalent to?

𝑠𝑝(𝑢, 𝑤) + 𝑠𝑝(𝑤, 𝑣)

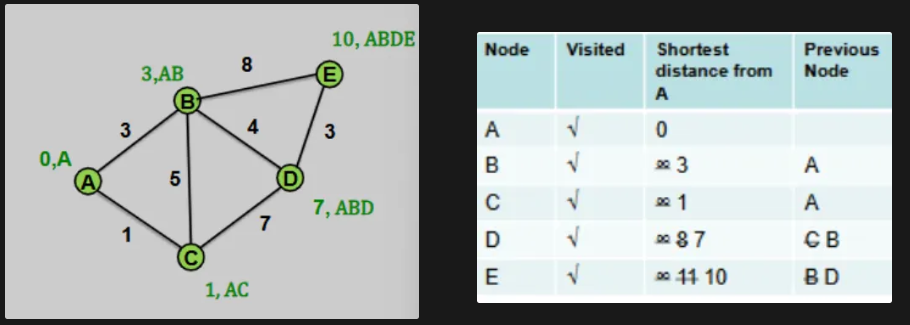
What is the algorithm for Dijkstras?

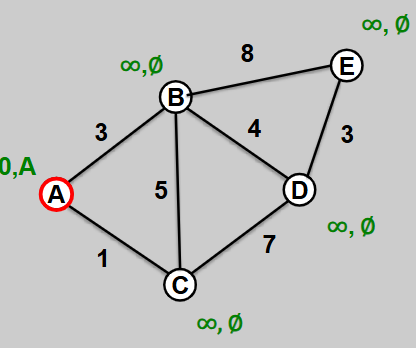
Perform Dijkstra’s on this graph:

What is the difference between the A* algorithm and Dijkstras?

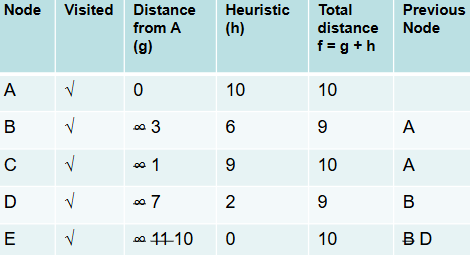
Uses the sum of the actual value and the heuristic value.

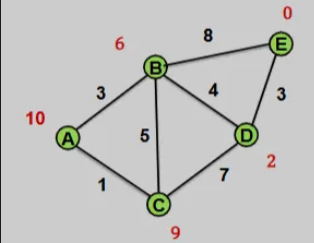
Perform the A* algorithm on this graph (given the red values are the heuristic values)

What is a spanning tree?

Is a tree which includes all vertices and uses only the minimum number of edges in the graph. All connected graphs have at least one spanning tree.

How many edges are in a spanning tree, given the number of vertices is n?

n-1

What is the minimum spanning tree?

The tree with the smallest weight

What is the pseudocode for the minimum spanning tree (Prim’s algorithm).

What is a greedy algorithm?

A problem-solving approach that makes the locally optimal choice at each step, hoping to find the global optimum, without considering the long-term implications of those choices

What is the complexity of Prim’s algorithm?

O(n³) as there are potentially O(n²) edges.

What is an intractable problem?

A problem where the best algorithm is Ω(n^c)∀c is super-polynomial in complexity

What is a tractable problem?

A problem where there is an algorithm that takes polynomial time O(n^c) time for constant c

What is a Hamiltonian path?

A path in the graph which visits all vertices exactly once.

Why is a Hamiltonian path intractable?

The best-known algorithms are Ω n^c ∀c, i.e. there is no polynomial time algorithm.

What is the travelling salesman problem (TSP)?

a travelling salesman must visit a set of cities and return to the start, while minimising the distance travelled. This problem can be represented on a graph – the cities are the vertices, and the edge weights represent travelling distances between cities. The problem is then to find a closed path (called a cycle) with minimum cost.
This is another NP-hard problem with all known
solutions having super-polynomial complexity.