Stacks Algorithms

the two steps of analysis of a source program (ex. an arithmetic expression)

1. lexical

2. syntactical

lexical analysis (scanning)

the source code is read from left to right (LR scan) and the characters are regrouped into tokens, which are successive characters that constitute numbers or identifiers.

• spaces are also supposed to be removed from the input during lexical analysis

• see example in image

syntactical analysis (parsing)

consists in regrouping the tokens into grammatical units, for example the sub-expressions of RPN expressions

scan() (for left-to-right scan)

eval (tokens from left to right)

evaluating an arithmetic expression: LR scan

• only works if every operator is sandwiched b/w nums

• ex: 3 + 4 - 5

• first round would have L = 3, OP = +, and R = 4

• L = result, so from the first round, L = 7

• next round would have L = 7, OP = -, and R = 5

• L is set = to result, so from the second round, L = 2

• now that you have reached the end of the expression, the while loop is exited from and the evaluation ends with 2 being the result

• however, L-to-R evaluation does not account for parentheses in arithmetic expressions OR the proper order of operations (ex. 2 + 4 × 7)

• so we need to either use diff notation or develop more complex algos, both of which necessitates stacks

notations: 3 ways to rep the expression L OP R

1. infix

2. postfix

3. prefix

notation: infix

this is the usual notation, the operator is sandwiched in between its operands: L OP R

ex. 8 + 4 × 6

notation: postfix

• operands (generally numbers) are placed BEFORE the operators

• ex. 7 - (3 - 2) → 7 3 2 - -

• ex. (7 - 3) - 2 → 7 3 - 2 - (notice how parentheses are interpreted)

• L R OP

notation: prefix

• consists of placing the operator before the operands

• OP L R

• ex. : (- 7 (* 3 2))

convert from infix → postfix (the idea / process)

• starting with the innermost bracket, L OP R is converted to L R OP

• postfix means the operator comes after the numbers

• then, brackets that contain their own expressions are treated like either L or R

• process repeats until you reach the whole expression

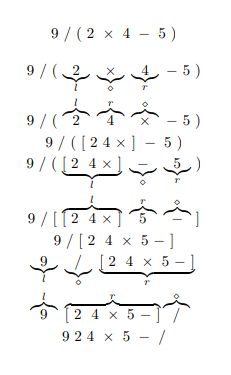
evaluating a postfix expression

1. from left to right *until the first operator*

2. apply the operator to the two preceding operands

3. replace the operator and its operands by the result

infix vs postfix

• infix requires the explicit handling of operators precedence and parenthesis

• but for postfix, those two concepts are embedded in the expression

• since like in the image, the expression is converted to postfix notation starting from inside the innermost bracket and working outwards

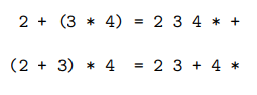
algo for evaluating postfix arithmetic expression

• the last statement is when all the operands have been eval’d and the result is stored in the operands array

• pop out RIGHT before left

postfix → infix