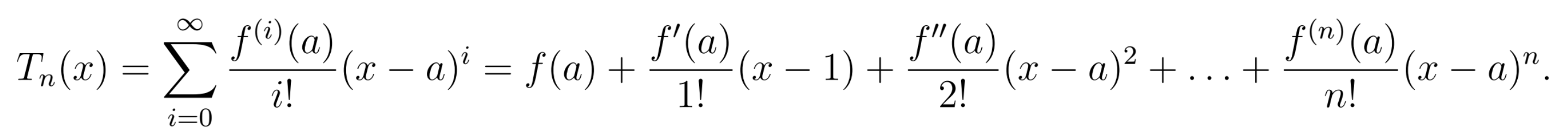Power Series, Taylor Series, Maclaurin Series

Power Series

A power series centered at a is a series of the form

a is some number
when a is zero the form just looks like c_n xⁿ

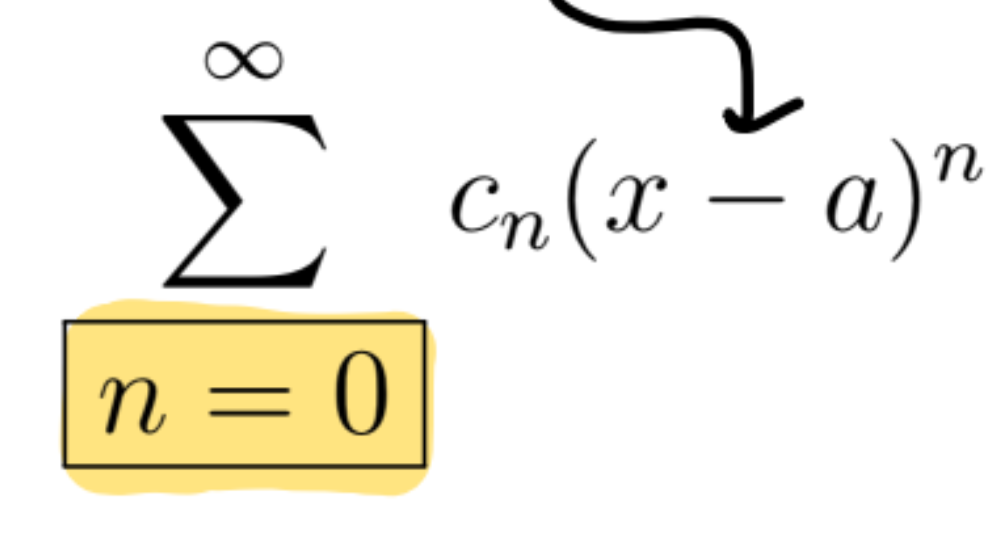
Power Series

A power series may…

1. converge for all x

2. converge for | x - a | < R, diverge for | x - a | > R

3. converge only for x = a, diverge for all other values of x.

R = radius of convergence

Power Series

The interval of convergence may be…

1. I = (-∞, ∞)

2. I = [a - R, a + R] or [a - R, a + R) or (a - R, a + R] or (a -R, a + R)

3. Just a point I = {a}, radius of convergence R = 0

Power Series

To determine convergence…

STEP 1: Determine the radius of convergence (by the ratio test).

STEP 2: Determine what happens at the endpoints (by tests other than the ratio test). Plug in endpoints (x-values) into the original series.

Taylor Series Expansion

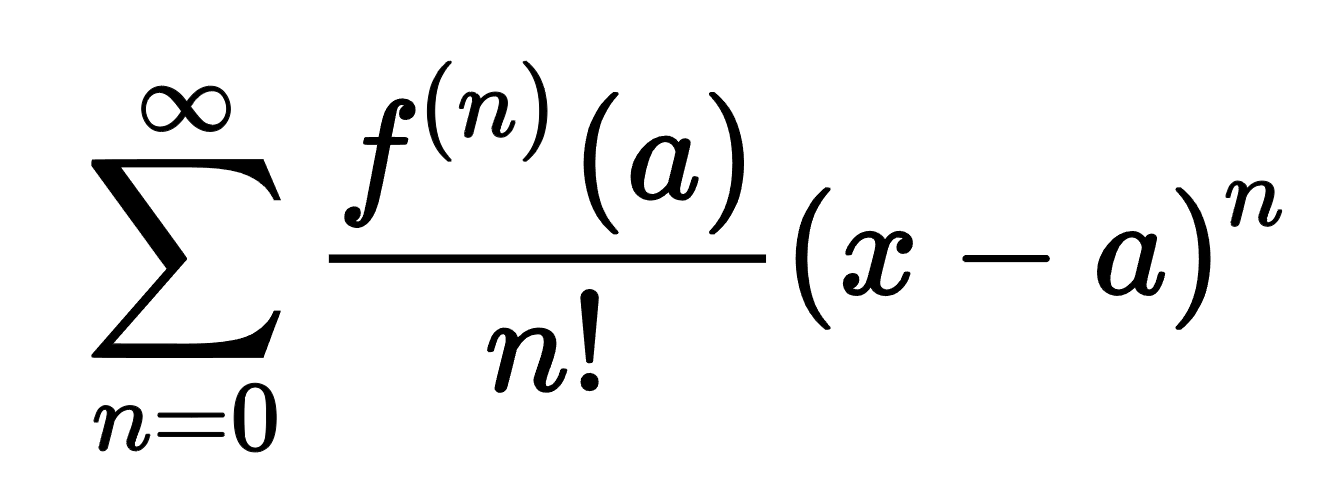
Maclaurin Series Expansion

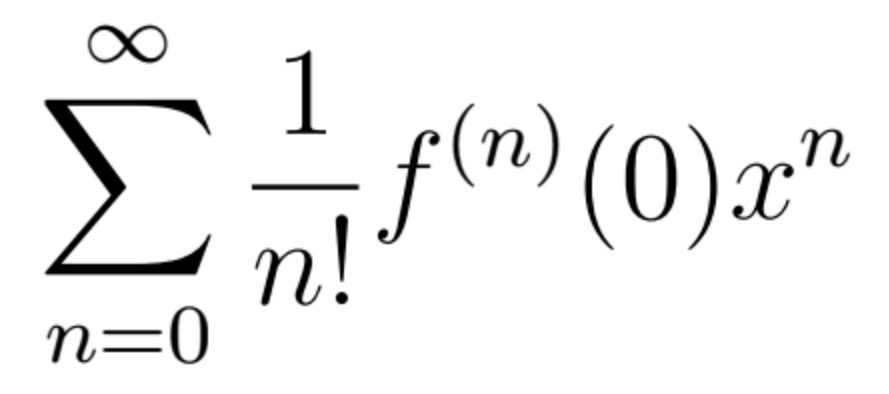
Method for expanding series from funcitons

Determine if you are making a Taylor Series or Maclaurin Series

Write out f(x) = series expansion of Taylor or Maclaurin around a

Find derivatives of function usually up to 5th derivative (n=5). Then plug in a to the derivatives.

Write out the sum of the series with found derivatives

Find pattern to determine series for the function

Taylor Polynomial

Taylor Approximation

Partial sum = Taylor polynomial
Find T_n(x) by computing derivatives and writing out partial sum up to the n^th degree