Charged Particle’s Motion in a Magnetic Field

force

A charged particle experiences a _____ when moving through a magnetic field

perpendicular

The simplest case occurs when the charged particle moves ____________ to a uniform magnetic field.

Magnetic field

What is the dominant factor on the charge determining its motion if the field is in a vacuum?

curved path, circle

When the magnetic force is perpendicular to the particle’s direction of travel, a charge particle follows a ___________ in a magnetic field, and continues util it forms a complete _____

Magnetic force does no work on the charged particle.

The magnetic force is always perpendicular to the velocity of the charge, therefore…

Particle’s kinetic energy and speed.

Things about the particle that remain constant when a charged particle moves perpendicular to a uniform magnetic field.

Particle’s direction of motion

Thing about the particle that does gets affected when it moves perpendicular to a uniform magnetic field.

Uniform circular motion

The result of the magnetic force being perpendicular to the velocity of the particle where the particle’s velocity is changing only in direction but not in the magnitude.

Negative

The charge on which when we apply the RHR-1, its force will be opposite in direction to our RHR-1’s prediction.

Fc = (m*(v^2))/r

Mathematical representation of the Centripetal force

F = q*v*B

Formula for the magnitude of the magnetic force

qvB = (m*(v^2))/r

Equation to write when a magnetic force is the one that is supplying the centripetal force.

r = (mv)/(qB)

Formula for the radius of the circle created by that charged particle traveling where the magnetic force is perpendicular to the particle’s velocity.

Period

The time for the charged particle to go around the circular path, which is same as the distance travelled (circumference) divided by the speed

T = (2πr)/v = (2π/v)*(mv/qB) = (2πm/qB)

Formula of the Period with its derivation when the particle’s velocity is perpendicular to the magnetic field.

Particle’s velocity is not perpendicular to the magnetic field

To compare each component of the velocity separately with the magnetic field if…

vperp = v*sin(θ)

Formula to calculate the velocity component perpendicular to magnetic field

vpara = v*cos(θ)

Formula to calculate the velocity component perpendicular to magnetic field

θ

Symbol that represents the angle between the particle’s velocity and the magnetic field

vperp

The component of the velocity that creates the constant motion along the same direction as the magnetic field.

Helix

Represents a rolled curve on a 3-D graph

Pitch (p)

The distance between the adjacent turns in the helix.

Basically a horizontal distance between two consecutive circles.

vpara

The velocity component that determines the pitch of the helix.

Basically moves the particle along a straight line.

Helical motion

The type of motion made by the charged particle when its velocity is not perpendicular to the magnetic field

p = vpara*T

Formula to calculate the pitch of helix

The particle is trapped in a magnetic bottle

While the charged particle travels in a helical path, it may enter a region where the magnetic field isn’t uniform.

Traveling from strong B region to weak B region and then back again to strong B region

Particle may reflect back before entering the stronger magnetic field

In this case the reflection happens at both ends.

North Pole

(1)

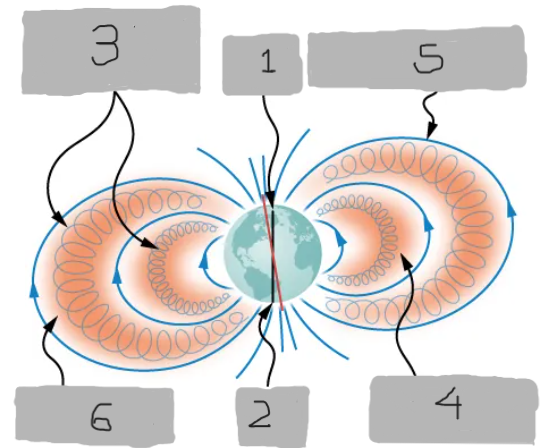
South Pole

(2)

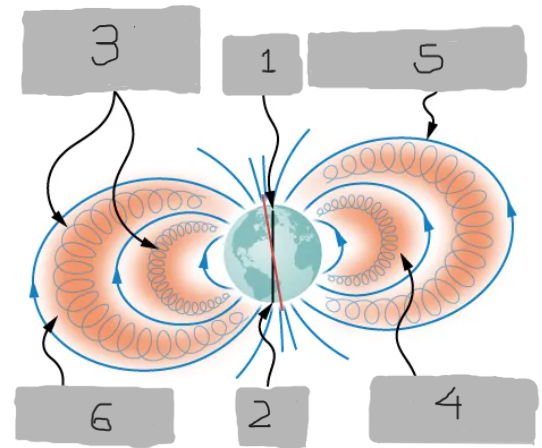
Charged particles trapped within van Allen belts

(3)

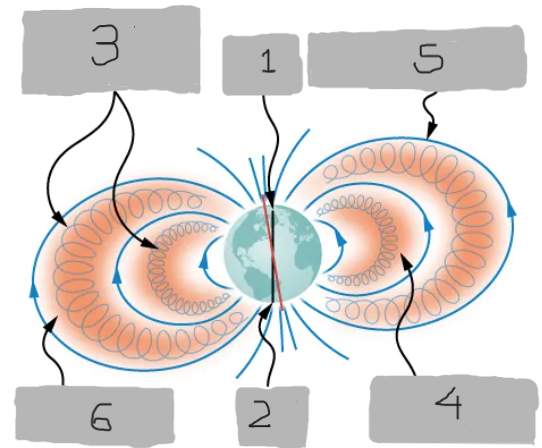
Inner van Allen belt

(4)

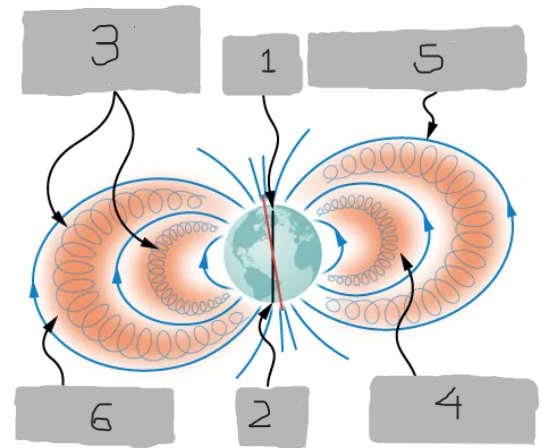
Earth’s magnetic field

(5)

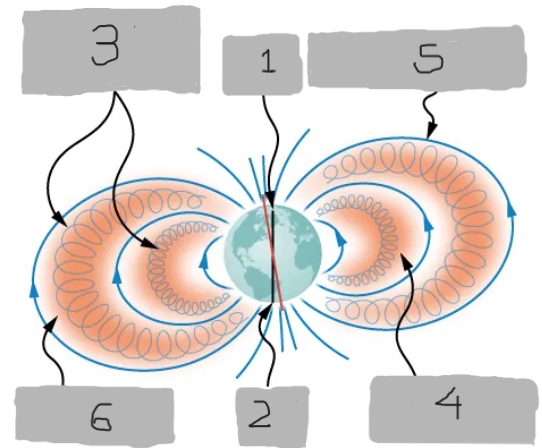
Outer van Allen belt

(6)

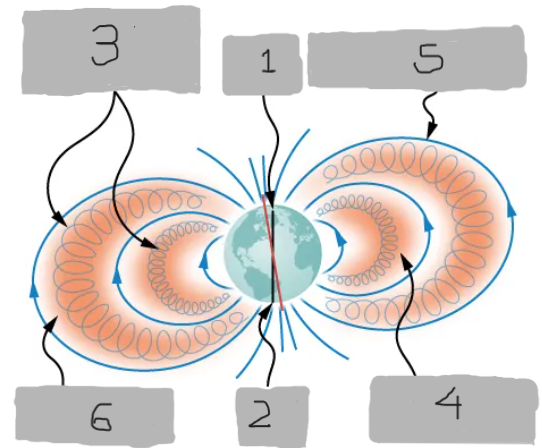
Van Allen radiation belts

Zones of charged particles trapped by Earth’s magnetic field, discovered around Earth.

James Van Allen

An American physicist who discovered the Van Allen radiation belts while trying to measure the flux of cosmic rays on Earth to see whether this was similar to the flux measured on Earth.

Cosmic Rays

High-energy particles originating from outside the solar system that enter Earth’s atmosphere.

higher, outer space, trapped

The flux of cosmic rays measured on Earth is much ______ than in __________ because of the contribution of particles _______ in Earth’s magnetic field.

Aurorae

Natural light displays such as (Northern Lights i.e Aurora Borealis)

They are caused when ions recombine with electrons as they move along the Earth’s Magnetic Field lines.

Oxygen and Nitrogen

Which elements’ atoms are primarily ionized by the energy particle collisions in the Earth’s atmosphere, leading to the formation of Aurorae.

Aurora

The Roman goddess of dawn

Boreas

The Greek god of north wind.