OCR A A Level Chemistry Module 5
1/286
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
287 Terms
Equivalence point
The volume of one solution that reacts excatly with the volume of the other solution
End point of a titration
When [HIn] = [In-] (colour is a mixture of two colours in indicator equation)
Nitric acid formula
HNO3
Nitrous acid formula
HNO2
Zero order
When the concentration of a reactant has no effect on the rate
First order
When the rate depends on its concentration raised to the power of one (if x doubles, y doubles)
Second order
When the rate depends on its concentration raised to the power of two (if x tripled, y increases by nine) x2
Rate equation
Rate = k [A]^m [B]^n
rate constant (k)
Number that mathematically converts between rate of reaction and concentrations
Overall order of reaction
Overall effect of the concentrations of all reactants on the rate of reaction (sum of powers in equation)
Units for overall order = 0
Mol dm-3 s-1
Units for overall order = 1
S-1
Units for overall order = 2
Dm3 mol-1 s-1
Units for rate
Mol dm-3 s-1
Initial rate of reaction
Rate when t = 0 (draw tangent to curve at t = 0)
Two methods for continuous monitoring of reactions
Gas collection
Mass loss
Colour change
concentration time graph gradient
rate of reaction
zero order line on conc time graph
straight line, negative gradient
value of gradient = rate constant k
first order line on a conc time graph
downward curve with decreasing gradient over time
time taken for conc of reactant to half is constant (confirm first order using half lives)
second order line on a conc time graph
downward curve with a steeper gradient at start which tails off more slowly
hard to distinguish between first and second order so use value of half lives
if constant its first order if they're not constant its second order
half life (t1/2)
time taken for half of a reactant to be used up
exponential decay
when first order reactions have a constant half life with the concentration of reactant halving every half life
[x]0
initial concentration of x when t = 0
use can use a tangent on a conc-time graph to measure...
rate
how to calculate rate constant k from using tangents on a conc-time graph
rearrange equation
substitute value for rate and the conc at which this rate was measured
k rate constant units
s-1
calculating k using half life equations
k = ln2/t1/2
why are rate conc graphs so important
offer a route into the direct link between rate and conc in the rate equation
zero order line on a rate conc graph
horizontal straight line with zero gradient
rate = k
intercept on y axis gives k
first order line on a rate conc graph
straight line graph through origin
rate directly proportional to conc
rate constant = gradient of straight line
second order line on a rate conc graph
upward curve with increasing gradient
rate constant cannot be obtained directly from graph
plot second graph of rate against concentration squared - straight line through orgin
gradient of this second graph is equal to rate constant k
initial rate
instantaneous rate at the start of a reaction when time = 0
clock reaction
more convenient way of obtaining initial rate of a reaction by taking single measurement
time (t) from start of experiment is measured for a visual change to be observed e.g. colour/precipitate
assumed that average rate of reaction over this time is equal to initial rate
initial rate proportional to 1/t
repeated several times at different concentrations and values of 1/t calculated
iodine clock
formation of iodine
starch usually added as gives more distinct colour change from orange to black
sodium thiosulfate Na2S2O3 removes iodine as it forms then when used up iodine forms
graph of 1/t against conc plotted
thiosulfate ions react with iodine forming I- ions which are not coloured when all thiosulphate reactions I- will build up in solution cauing colour change as i2 is formed
accuracy of clock reactions
in these reations you are measuring average rate during first part of the reaction
over this time you can assume that average rate of reaction is constant and thus same as initial rate
the shorter the period of time measured the less the rate changes and hence more accurate
reasonably accurate providing less than 15% of reaction has taken place
reaction mechanism
series of steps that make up overall reaction
rate determining step
slowest step in a multi step reaction
rules for rate equation/rate determining step
rate equation only involves species involved in the rate determining step
orders in the rate equation match the number of species involved in the rate determining step
effect of temperature on rate constant
as temp increases, rate increases and so k will increase
each 10 degrees rise in temp rate constant doubles
two factors which contribute to higher rate constant at higher temps
Boltzmann distribution shifted to the right increasing proportion of particles that exceed Ea
particles move faster and collide more frequently (higher ke) this factor is comparatively small compared with right shift so change in rate mainly governed by Ea
the Arrhenius equation
k = Ae-eA/RT
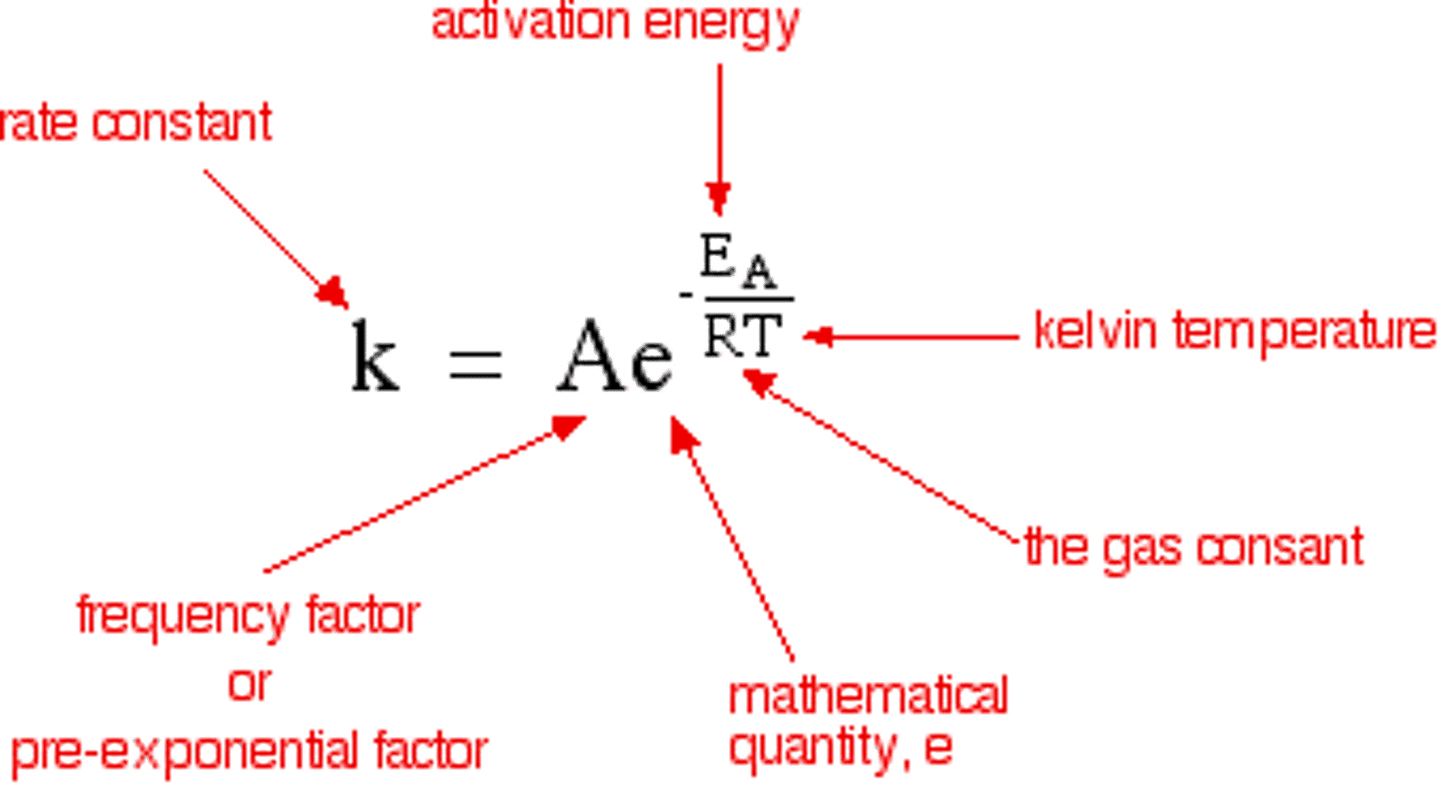
exponential factor e-Ea/RT represents ...
the proportion of molecules that exceed Ea and have sufficient energy for a reaction to take place
pre exponential term A
takes into account the frequency of collisions with the correct orientation gives rate if there was no activation energy
Logarithmic form of the Arrhenius equation
lnk = -Ea/RT + lnA
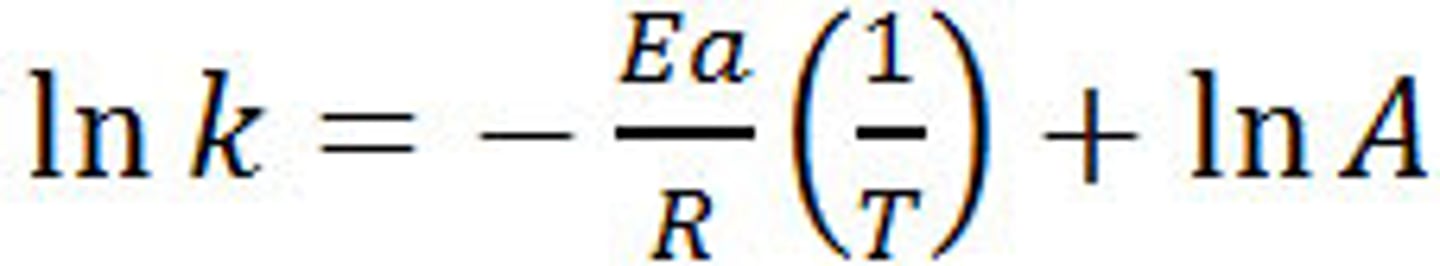
Arrhenius equation graph
plot ln k against 1/t
straight line graph
gradient = -Ea/R
intercept = ln A
equation for Kc
conc of products/conc of reactants
raised to the power of their stoichiometric numbers
value of kc and position of equilibrium
larger the value, the further the position of equilibrium to the products
smaller the value, the further the position of equilibrium towards the reactants
units of kc
substitute units into expression for kc
cancel common units
homogenous equilibria
equilibrium species that all have the same phase e.g. gas
heterogeneous equilibria
equilibrium species that have different phases
any species that are solid or aqueous are omitted from the Kc expression
calculating equilibrium concentrations
equilibrium amounts in mol / total volume
Kp used in
equilibria involving gases
easier to measure pressure than conc of gases
mole fraction
number of moles of gas x/total number of moles in gas mixture
sum of mole fractions always =...
1
partial pressure
mole fraction x total pressure
sum of partial pressures always = ...
total pressure in question
what values are used in Kp expression?
small p(x) is equilibrium partial pressure
calculating Kp steps
calculate total number of gas moles
calculate mole fractions of each gas
calculate partial pressure of each gas
substitute into kp expression use units given in question
Value of equilibrium constant K gives ...
exact position of equilibrium
at a set temp... does conc, pressure or catalyst change value of K?
no
what is the only condition which changes value of k
temperature change
effect of temp on k explained
if forwards reaction is exothermic an increase in temp will decrease value of k as raising temp decreases eqm yield of products/pos of e shifts to the left
if the fwd reaction is endothermic the eqm constant k increases with increasing temp as raising temp increases eqm yield of products as partial pressure of products must increase to match kp
explain the non change to kp/kc with changing conc/pressure
kp/kc stays constant but ratio doesn't match so must change to restore eqm
effect of catalyst on p.o.e
catalysts affect/alter the rate of a chemical reaction but not the p.o.e
catalysts speed up both forward and backward reactions by same factor to reach eqm quicker
bronsted lowry acid
proton donor
bronsted lowry base
proton acceptor
alkali
soluble base that releases OH- ions in aqueous solution
Strong base
Alkali that completely dissociates in aq solution
conjugate acid base pair
two species interconverted by transfer of a proton
hydronium ion
H30+
conjugate acid of H2O
Monobasic acid
an acid that has only one hydrogen ion to donate to a base in an acid-base reaction. Therefore, a monobasic molecule has only one replaceable hydrogen atom
Dibasic acid
2x h+ ions can be replaced
how to tell if an acid is mono etc
count number of hydrogen atoms in formula not including organic carbon chains
writing equations for complete neutralisation
determine whether mono di or tri
write equation using as many base units needed to neutralise number of h
these can be used to calculate volume needed to neutralise a set volume of acid
if mono then same
if di then double
if tri then triple
spectator ions
ions that do not change over course of reaction they are removed when constructing ionic equations
redox reactions between acids and metals
produces salts and hydrogen gas
neutralisation of acids with carbonates
forms salt water and carbon dioxide
neutralisation of acids with metal oxides
forms salt and water only
neutralisation of acids with alkalis
same for metal oxides forms salt and water only just in solution
why is a negative logarithm used when measuring ph
makes scale more manageable
pH =
-log[H+]
[H+] =
10^-pH
ph of one has ... the conc of h+ ions than a solution of ph 2
10x
strong acid ph calculation
[H+] = [HA]
Stong acids
Nitric (HNO3)
HCL
H2SO4
Stong acid
completely dissociated in aqueous solution
weak acid
partially dissociates in aqueous solution
acid dissociation constant Ka
[H+][A-]/[HA]
Factors affecting Ka
Temperature
pKa =
-log(Ka)
Ka =
10^-pKa
low pka =
stronger acid
Weak acid equilibrium
ha <-> h+ + a-
[H+] depends on ..
concentration of acid
acid dissociation constant ka
When HA dissociates, H+ and A- are formed in ...
Equal quantities
Approximations for calc Ph of weak acids
1) H+ conc from dissociation of water very small compared to H+ from HA and so neglected
2) HA start much much greater than H+ at eqm due to partial dissociation so neglect any decrease in conc of HA so HA start = HA eqm
Simplified Ka expression after approximations
Ka = [H+]2/[HA]start
Finding H+ /ph of weak acid (expression)
[H+] = square root of Ka x [HA]
Experimentally determining Ka for weak acid
Prepare standard solution of weak acid at a known concentration
Measure ph of standard solution using ph meter
Breakdown of approximations involving weak acids
1) if pH is greater than 6 then dissociation of water will be significant compared with dissociation of weak acid so approximation breaks down for very weak acids or very dilute solutions
2) when [H+] becomes significant with stronger weak acids you cannot assume that [HA] is much much greater than [H+] as there is more dissociation (approx doesn't hold for acids with Ka over 10-2 or dilute solutions