COSC401 5: Generative Models & Feature Maps

Difference between discriminative and generative algorithms?

Discriminative models try to learn p(y|x) directly, or mappings from input space to output space {0,1}

Generative models try to model p(x|y) and p(y).

How to get p(y|x) from p(x|y) and p(y)

Bayes rule, where p(x) is also calculatable given what we know:

p(x) = p(x|y=1)p(y=1) + p(x|y=0)p(y=0)

Also, we don’t actually need to calculate p(x) when we are making a prediction since we can just find the y argmax of p(x|y)p(y)

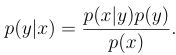
Motivation for feature maps

We sometimes need a more expressive family of models than linear models.

Feature maps phi allow us to view a cubic function of x for example, as a linear function over the variables phi(x)

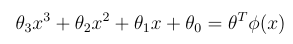
LMS with features

The exact same but replacing x(i) with phi(x(i))

Benefits of kernel trick

• no need to store large theta explicitly

• significant runtime improvement

When can theta be represented as a linear combination of the vectors phi(x(1)), … phi(x(n))?

At any time.

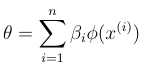
Explain:

We assume that at some point, theta can be represented as the image shows, for some beta_1, … , beta_n.

We claim in the next iteration, that theta is still a linear combination of phi(x(1)), … phi(x(n)), and then do some math magic to implicitly represent theta by the betas.

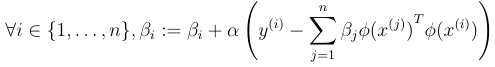
Two important properties of using the betas

1) we can pre-compute the pairwise inner products of the phis, for all pairs.

2) computing phi inner products can be efficient and does not require explicitly computing the phi(.) values.

• e.g. for up to 3 dimensions: the inner product of phi(x) and phi(z) is just 1 + the inner product of x and z + the inner product of x and z squared + same thing cubed.

• this take O(d) time (efficient as)

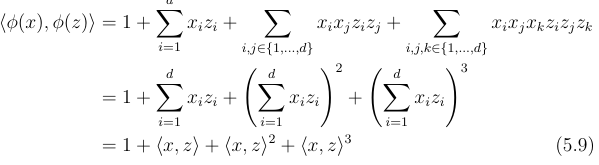
Final kernel trick algorithm?

1) compute all values K(x(i), x(j)) for all i, j in range(1, n + 1)

2) set initial beta to 0

3) loop beta update formula.

Time complexity for updating beta representation of theta?

O(n) per update.

What can kernels kind of be thought of?

A similarity metric.

• if phi(x) and phi(z) are close together, we might expect K(x, z) to be quite large

What 2 things must a kernel (matrix) be?

• symmetric

• positive semidefinite (all entries are >= 0)

What is the main assumption of Gaussian Discriminant Analysis GDA?

We assume p(x|y) is distributed multivariate normal

Parameters of GDA?

mean vector mu, and covariance matrix sigma.

What are the three assumed distributions?

y ~ Bernoulli(sigma)

x|y=0 ~ Normal(mu_0, SIGMA)

x|y=1 ~ Normal(mu_1, SIGMA)

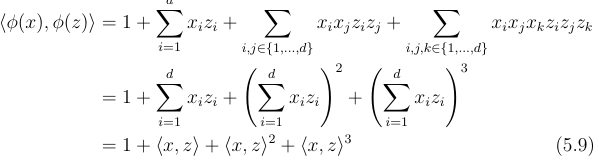
Do we maximise lof likelihood to estimate sigma, mu_0, mu_1, and SIGMA?

Yes.

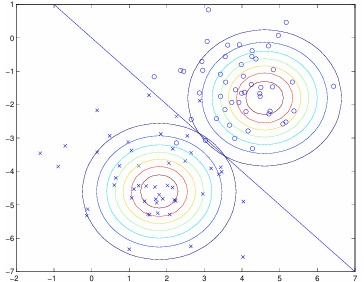
Compare GDA and logistic regression

Viewing p(y=1|x; sigma, mu_0, mu_1, SIGMA) as a function of x reveals a form exactly that of logistic regression (which is a DISCRIMINATIVE algorithm).

GDA implies log.reg., but the inverse is not true. Therefor, GDA makes stronger assumptions about the data, and when these assumptions are correct, it will find better fits with the data, and with less data required to do so.

Logistic regression making weaker assumptions makes it more robust and less sensitive to incorrect assumptions. In other words, there are different distributions that can also be modelled by log.reg. (e.g. Poisson(lambda)) that GDA cannot model.

In practice, log.reg. is used more.