The Rest of the Course (after Midterm 2)

cross product formula using cofactor row expansion

• don’t forget the minus sign written before the j (vertical component of the vector)

• rmbr: ai + bj + ck = (a, b, c)

formula for the curl of a vector field

• remember: ∇ × F (order is important)

• expand the top row via cofactor determinant expansion

curl of a vector field F = (P, Q, R): input and output

• computing the curl gives you another vector field

• the input of a curl = any point in space

• the output of a curl = a vector where the direction is the axis that the point is “spinning around” and the magnitude is how fast it is spinning

curl of a vector field: defn

• curl measures the infinitesimal circulation per unit area at a point

• imagine a tiny closed loop around a point in a vector field, computer the circulation (line integral of the vector field around that loop), divide by the area of the loop, and shrink the loop to size → 0, and the vector that you get is the curl at that point

right hand rule for curl

right hand rule for stokes theorem

the curl of a gradient, which is a type of vector field, is equal to ___

zero.

• gives criterion for determining whether a vector field is the gradient of some function

• so if you are given some vector field F, and you compute the curl with ∇ × F and it eqiuals to 0, then F = the gradient of some function and you can use the

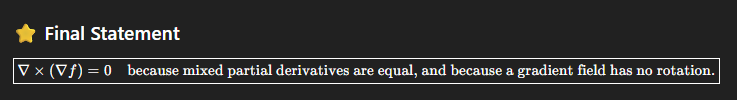
formula for the divergence of a vector field (in 2D)

just remember this dot product: DIV(F) = ∇ ⋅ F

formula for the divergence of a vector field (in 3D)

or just remember: DIV(F) = ∇ ⋅ F

divergence of a vector field: defn

• the computation of the divergence gives you a real number, not a vector

• if you imagine the vector field as a pool of water, divergence at a point tells you whether water is spreading out (called a source) or converging in (sink)

  • if divergence result at some point = positive → source

  • negative → sink

  • zero → neither source or sink

what is the computation of the divergence of a curl of a vector field equal to?

ZERO.

∇⋅ (∇ × F) = 0, because the dot product between perpen vecs = 0, and ∇ is perpen to (∇ × F) by defn of cross product

formula for green’s flux theorem

so instead of computing the left hand side, you can compute the right hand side IF green’s flux theorem applies, and the equation just becomes a normal double integral

• this theorem is only for 2D

• R = D = domain

• (∇ ⋅ F) = DIV(F)

criterion for the green’s flux theorem

1. the curve C that bounds the domain D just be a simple closed curve (it doesn’t cross itself)

2. C must be positively oriented (when traversed counterclockwise, D is always on your left)

3. D should be simply connected. if there are holes, it must be computed separately

what is the formula for flux of a parametric surface

flux of a surface: defn

formula for the normal vector in the flux formula

if you have a tangent vector <a,b>, what would the normal vector be?

n = <b, -a>

• only works for vectors that only have two components

if a curve is negatively oriented, what should you do?

include a minus sign in the formula

formula to find the unit normal

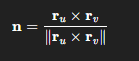
formula to finding the area of a surface

formula for integrating a function over a surface

if you were given the parametrization of a cylinder → (Rcosθ, Rsinθ, z), how do you make it a surface

make one of the variables a fixed number

• the most common is to make R into a fixed number → if R = 2, then you’d get the surface parametrization of r(u,v) = (2cos(u), 2sin(u), v) where u = θ and v = z….

formula for integrating a vector field over a surface

a shortcut when computing the integral of a vector field over a surface

• for when u = F (vector field)

• and v and w are the partial derivs of the parametrization of the surface

formula for stokes theorem

turns a complicated line integral into a simpler to compute surface integral

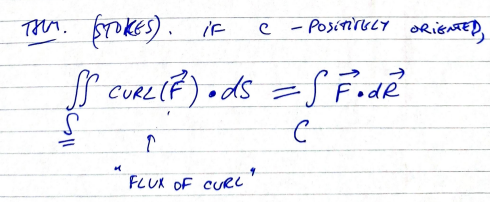
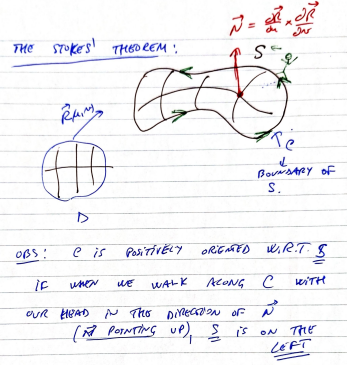
criterion for applying stokes theorem

when you look from the direction of the normal vector, you must walk around the boundary counterclockwise

formula for divergence theorem

this theorem makes it so you don’t have to compute a complicated surface integral, and you just have to compute a regular triple integral by treating the surface as the boundary of some volume

• best for surfaces with hard corners, like a cube

• the surface must be a CLOSED SMOOTH surface

• the normal vec (n) must be pointing outwards out of the surface. if it’s pointing inwards, you have to apply -1 to the integral