COM1009 Algorithms and Data Structures

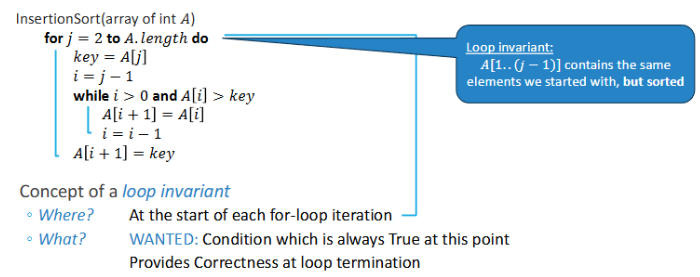
Insertion Sort Algorithm

Runtime:

• Best case: Sorted ascending => n-1

• Worst case: Sorted descending =>

Merge Sort

A divide and conquer algorithm that sorts an array by recursively dividing it into halves, sorting each half, and then merging the sorted halves back together.

Priority Queue Naïve Implementation

Each element x of a set M, has priority x.key. Array position containing the highest priority is at A[iM] which is checked each time an element is inserted into an array with a priority (Insert(priority p)), FindMax() returns A[iM]. ExtractMax() removes the element with highest priority and sets the new maximum as needed.

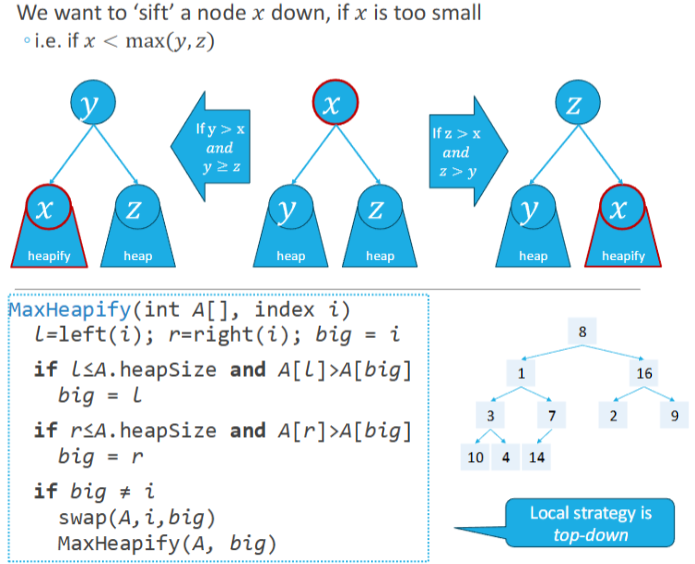
Heap

A heap is an array corresponding to a binary tree, for which all levels are full except the last and is filled left to right.

A heap ‘A’

• Has the max-heap property,, if…

• For every node i > 1

• A[parent(i)] >= A[i]

• Called a max-heap

• Has the min-heap property if…

• For every node i > 1

• A[parent(i)] <= A[i]

• Called a min-heap

MaxHeapify

Is a procedure to maintain the max-heap property in a binary heap. It ensures that the subtree rooted at a given node follows the property by comparing the node with its children and swapping if necessary.

Trees are stored in arrays where the child nodes of an element are at index x2 and index x2 +1

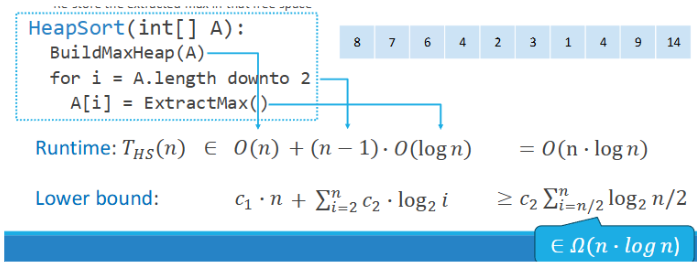
Heap Sort Algorithm

A comparison-based sorting algorithm that utilizes a binary heap data structure to sort elements. It first builds a max-heap from the input data and then repeatedly extracts the maximum element from the heap, placing it at the end of the sorted array.

Probability Modelling Trick

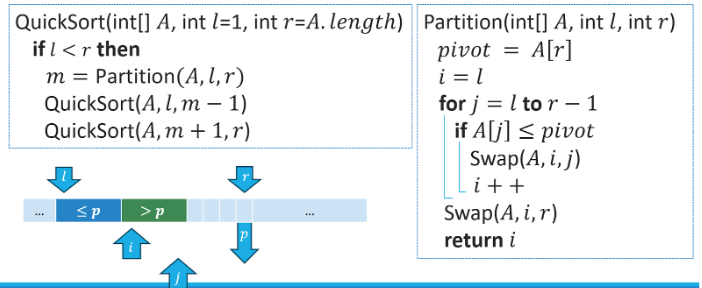
Quicksort

Growth Orders

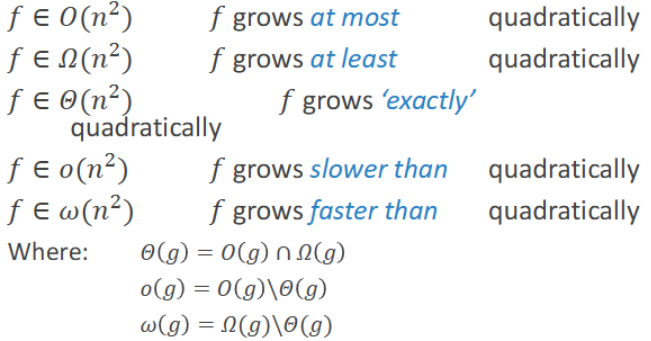
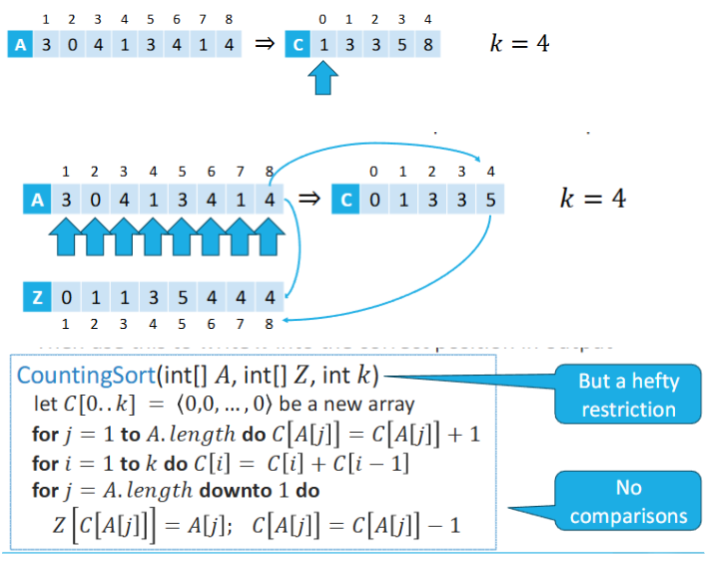
CountingSort

A linear time algorithm

• For every x of the input, count numbers <= x

• Use this to write x into correct position in output

• A - input array

• Z - output arrat

• C - work array (where we count)

• K - limit of the universe: {0,..,K}

Runtime for n numbers: O(n + k)

In-Order Traversal

• Recursively travel left subtree of the root

• Output value of the root

• Recursively traverse the right subtree of the root