Math Revision

point-slope form

(y -y) = m(x - x)

Vertex formula

x = -b/2a

completed square form

y = a(x - h)² + k, where vertex = (h,k)

factorized form

a(x - p)(x - q) = y, where p and q are x-intercepts

the axis of symmetry is x = (p + q)/2

completing the square

when y = bx + c

completed square: y = (x + b/2)² - (b/2)² + c

cutting

2 points of intersection, if the line touches the curve at least once, it is a tangent to the curve

touching

1 point of intersection, if the line touches the curve at least once, it is a tangent to the curve

missing

0 points of intersection

natural domain of f(x) = x²

x ∈ R

natural domain of f(x) = √x

x ≥ 0

natural domain of f(x) = 1/x

x ≠ 0

natural domain of f(x) = 1/√x

x > 0

many to one function

there are multiple inputs to the same output (e.g. parabola), does not pass horizontal line test

inverse is not a function

one to one function

every x goes to a unique y (e.g. straight line), passes horizontal line test.

inverse is a function

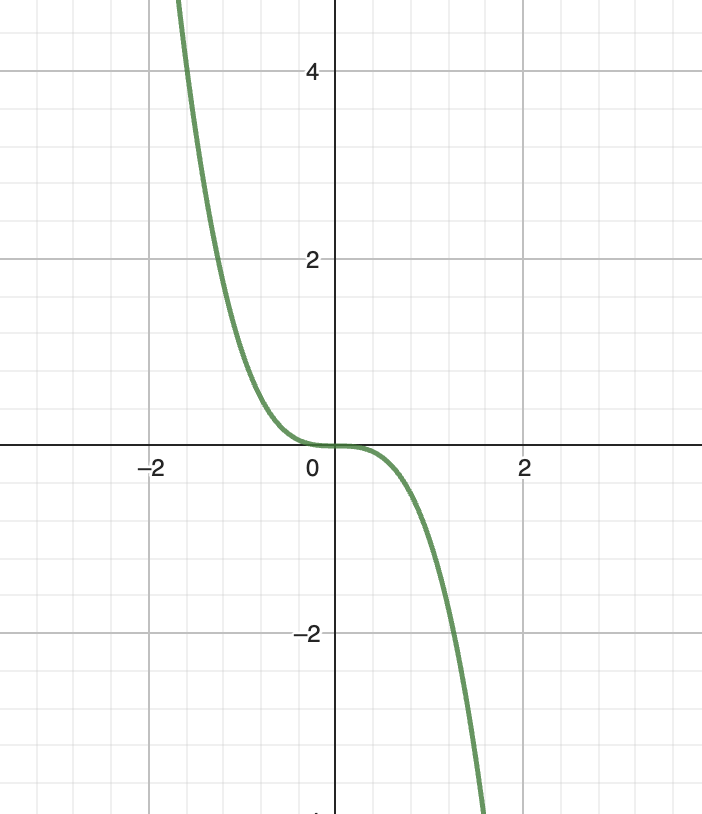
graph of f(x) = x³

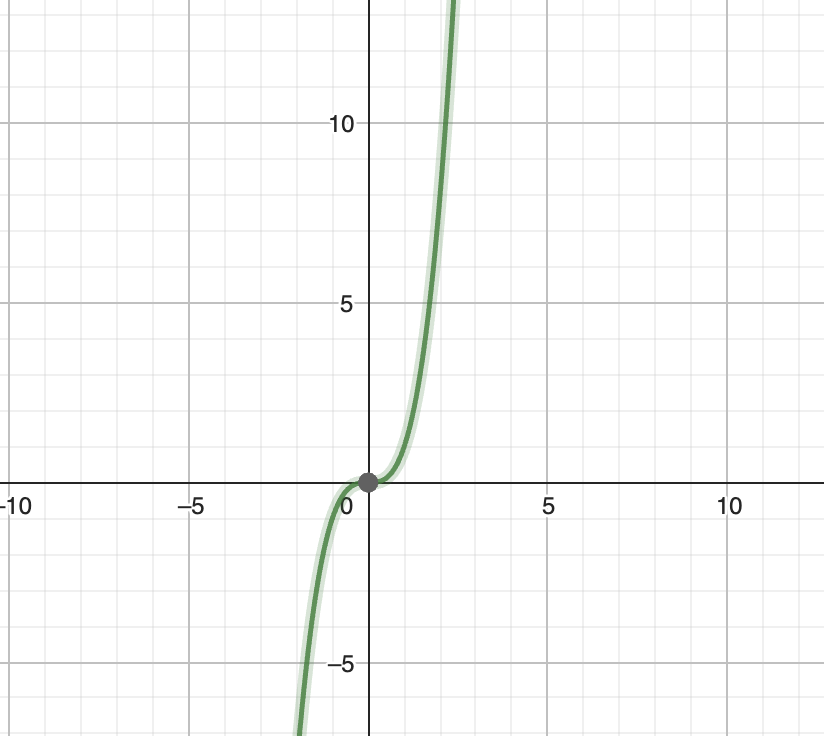
graph of f(x) = -x³

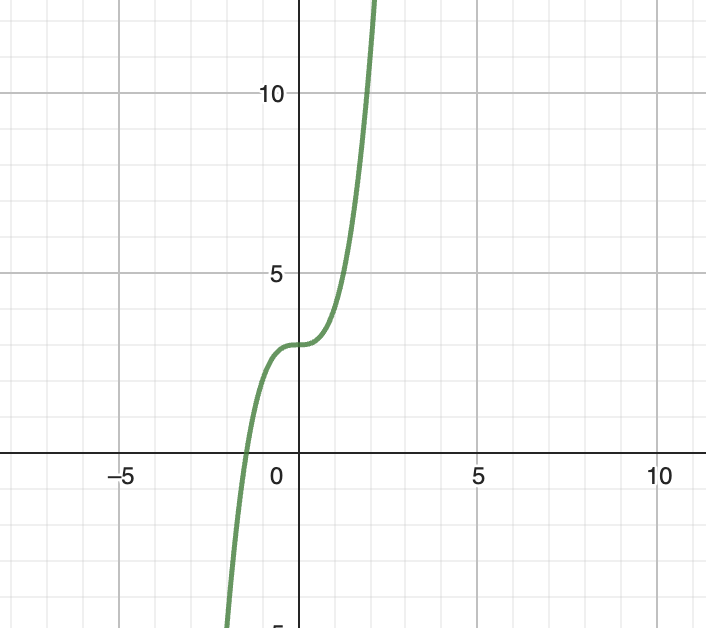
graph of f(x) = x³ + anything

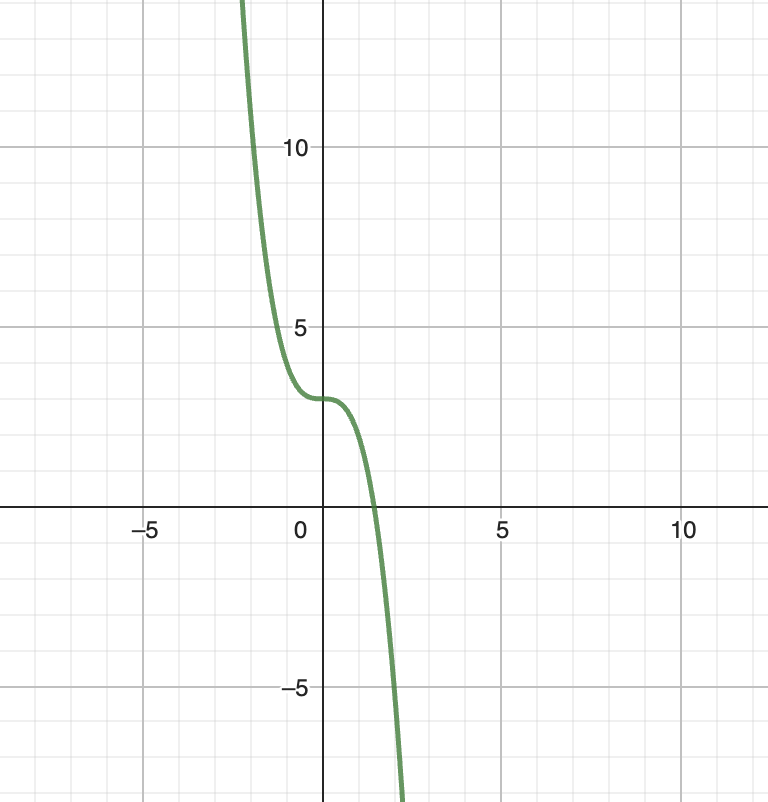
graph of f(x) = -x³ + anything

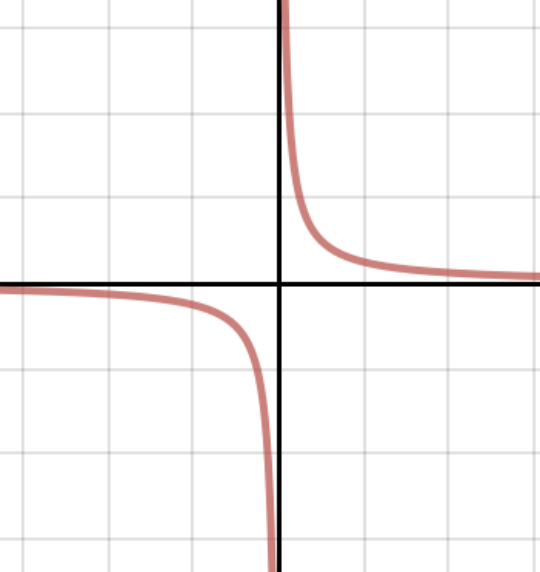
reciprocal function

a function of the form y = k/x, where k ≠ 0

graph is a rectangular hyperbola which has…

• 2 branches

• a horizontal and vertical asymptote

• the coordinates of points on the asymptotes are (1,k), (k,1), and (-k,-1), (-1,-k)

• if you increase k, the curve becomes flatter as the graph moves further from the origin

asymptotes for function in form y = b/(cx + d) + a, where b & c ≠ 0

vertical asymptote: x = -d/c

horizontal asymptote: y = a

asymptotes for function in form y = (ax + b)/(cx + d), where c ≠ 0

vertical asymptote: -d/c

horizontal asymptote: a/c

if y = undefined for the domain in f^-1(x)…

y = ∞

to solve 3^x = 10…

find the intersection between f₁(x) = 3^x and f₂(x) = 10. The x-coordinate is the answer.

Characteristics of exponent graphs…

• Go through (0,1)

• On either side of (0,1) the biggest/smallest values switch

• If the exponent is negative (e.g. 2^-x) the graph is a reflection

Exponent graph formula

y = pa^x-h + k

• k controls vertical movement (+ve = up)

• h controls horizontal movement (+ve = left)

• a controls how steeply the graph ascends

• if p > 0, the function is increasing (reverse is true)

Area of a trapezoid

A = (a + b) / 2 x h

Area of a sector

A = θ/2 x r²

where θ is in radians

Ambiguous case

2 angles that add up to 180 have the same sin value

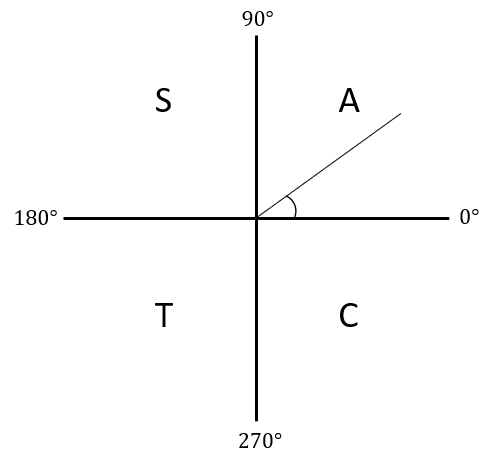
CAST diagram

• Cos ratios positive

• All ratios positive

• Sin ratios positive

• Tan ratios positive

Hand trick

sin(angle) = √(number of fingers remaining)/2

sin = fingers on the left

cos = fingers on the right

Translation down by 1 unit

f(x) - 1 = x + 4

Translation left by 1 unit

f(x + 1) = x + 4

Reflection in the x-axis

y = -f(x)

Reflection in the y-axis

y = f(-x)

Enlargement in the x-direction

y = f(ax), enlargement b scale factor a

Enlargement in the y-direction

y = af(x), enlargement by scale factor a