Graph Theory Cont'd

defn of a bipartite graph

A graph G is bipartite when their vertex set can be divided into two disjoint sets U and V such that no two vertices within the same set are adjacent.

• no vertices in set U are adjacent in the orig graph and same goes for set V

• vertices in set U are adjacent to vertices in set V

a graph G is bipartite if and only if ___

none of the subgraphs of G are isomorphic to a cycle of odd length.

• no odd cycle (C1, C3, C5.. etc) is bipartite

• ALL even cycles are bipartite

• any graph that HAS AN ODD CYCLE AS A SUBGRAPH is NOT bipartite

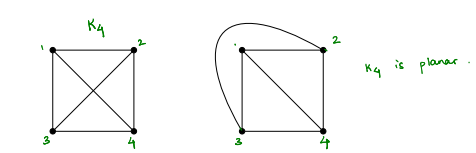
defn of a planar graph

A graph G is planar if it can be drawn on the plane without any intersecting edges. Such a drawing is called a planar embedding of G.

example of a planar graph and a planar embedding of a graph

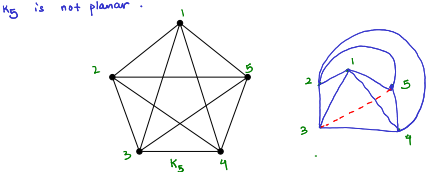
example of a non-planar graph

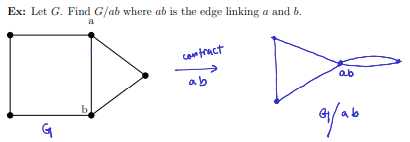
defn of “contract”

to contract an edge e of a graph G is to remove e, and fuse together the vertices incident to e.

• the resulting graph is denoted G/e.

visual of contracting an edge

if G is planar and v is a vertex of G, then G - v is ____

planar

• G - v means to delete the vertex v AND ALL edges incident to it

If G is planar and ab is an edge of G, then G - ab is ______

planar

• G - ab means to remove the edge ab (not contracting it)

If G is planar and ab is an edge of G, then G/ab is _______

planar

• G/ab means to contract the edge ab

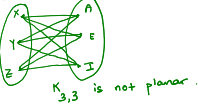
A graph G is not planar if and only if:

K5 or K3,3 can be obtained from G via a sequence of vertex deletions, edge deletions and edge contractions.

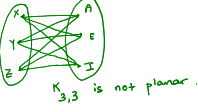
K3,3

K5

defn of “colouring a graph”

let G be a graph. A colouring of G is a way of assigning a colour to every vertex of G such that any two adjacent vertices receive different colours.

• the min num of colours needed to colour G (and satisfy the above stipulation) is the CHROMATIC number of G

chromatic number

the minimum number of colours needed to colour G is the chromatic number of G, denoted by χ(G).

how to obtain the chromatic number of a graph G

a colouring of G = (V, E) (which is (# of vertices, # of edges)) with n colours is a function f : V (set of vertices in G) → {1, 2, ..., n} (set of natural numbers up to n) such that if a is adjacent to b, then f(a) ̸= f(b) (they don’t share the same colour)

• the set of natural numbers are the numbers assigned to distinct colours (ex: 1 = red)

if H is a subgraph of G, then

χ(H) ≤ χ(G). (the # of colours needed to colour H is less than the # of colours needed to colour G)

• Any colouring of G with χ(G) colours generates a colouring of H with at most χ(G) colours.

χ(Kn) =

n

χ(Cn) = ___ if n is ____, and χ(Cn) = ___ if n is ____

2; even; 3; odd

method to colour a graph (2 steps)

1. Sort the vertices of G in an arbitrary order v1, v2, v3, ..., vn.

2. Colour the vertices of G, one by one, in the given order, by assigning to v_i the smallest possible colour (colour 1, for example) at each step

let G = (V,E) be a graph, and let ∆ = max{deg(v) | v ∈ V}, then

χ(G) ≤ ∆ + 1

meaning the chromatic num of the graph <= biggest deg + 1

chromatic poly

→ gives the ways to colour a graph with [symbol] colours in a formula