Theory of Computation

computer systems, abstraction, decomposition, pattern recognition, algorithms, information hiding

define computation

processing something through mathematical/ logical/ interactive methods

define computability

measures what can/ can’t be processed

(non-computable programs = programs that can NEVER be processed)

define logical reasoning

using a set of facts to determine if new facts are true/ false

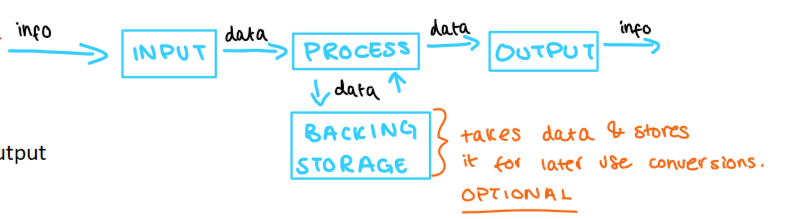
what are the basic components of a computer system?

• convert human input to binary

• computer processes binary data

• binary data converted to ascii output

what are the 4 components that make up computational thinking

abstraction

decomposition

pattern recognition

algorithm

define abstraction

taking most important components needed to solve problem & separating them from rest

define decomposition

breaking down problem into smaller (easier to solve) sub programs

define pattern recognition

finding similar approaches to solve problem and adapt them to solve current one

define algorithm

representing solution as a sequence of steps (step by step instructions needed to solve problem)

how do computers work? basic

an algorithm is run on a computer by translating it into a sequence of computer instructions

this is converted to binary (uses switches for 1s and 0s) where computer reacts to voltages on wires

what does it mean to automate a program?

automation: idea that computer programmer turns algorithm into computer program for computer to execute

e.g. paint onto car

three types of abstraction

• representational abstraction

• abstraction by generalisation

• problem abstraction

what is abstraction by generalisation

reducing problem by putting similar aspects of the problem into hierarchical categories

explain problem abstraction and give an example

removing unnecessary details until underlying problem is identified to see if it has already been solved

e.g. pigeon hole principle

what is representation abstraction

removing details from problem until it becomes possible to represent problem in a way that it is possible to solve

what is the purpose of user interface?

• hides complexity of program

• easily operate computer

• users are satisfied

• makes program more popular

define information hiding and describe its uses in programming

• hides details of object which do not contribute to essential characteristics

• In programming:

  • Well designed program has a solution in which source code is divided into self-contained modules. Programmer works on module so do not need to know all detail contained in other programmer modules. This makes it easier as they are local rather than global changes.

  • Function age(DofB as date, today as date) as integer

describe decomposition with an example

top-down design: modular approach where main system is at top and then broken down into smaller & smaller units

procedural decomposition: problem is divided into smaller parts and then solved independently. they are then written and tested separately before being integrated into the larger problem

benefits of using decomposition:

• starting point in the aim of a project

  • helps users and the system analysts reach an early agreement about what the major functions should be

• works through ‘logical’ design

  • not restricted by ‘physical’ attributes of programming language

  • result is more portable designs

why is procedural decomposition helpful?

• makes programs more modular

• easier to:

  • understand

  • debug

  • maintain

outline modular design:

• number of small modules are written

• each module has a clear objective/ specific function

• each module may be a complete system in itself/ an executable file or subroutine

• they are independently designed, programmed and maintained

• modules are then put together in a larger structure

• each module will have a single entry-entry and exit point

• + can be easier to program

• - may result in an inefficient system

• - project can veer towards a bottom-up design

clear advantages for using modular design

• separate programmers can be working on modules individually

• programmer is only concerned for their part of the system so programming is easier

• flow of data can be traced far more easily through program

• debugging is made easier as errors can be traced back to a single module

define computational complexity

how economic the algorithm is with time and space

why is computational complexity used?

allows us to compare algorithms as there may be multiple algorithms for achieving a solution to a problem and they may vary considerably in their speed and use of memory

time complexity

algorithm indicates how fast it runs

space complexity

algorithm indicates how much memory algorithm needs (memory footprint)

worst case complexity

algorithm takes longest time or greatest workload

best case complexity

algorithm takes shortest time or smallest workload

how is average case complexity calculated

calculating arithmetic mean for all possible inputs

describe the 2 ways of measuring complexity of algorithm and evaluate

• algorithm written in programming language an then run on computer and timed

  • CRUDE way because it is dependent on:

    • speed of computer

    • efficiency of programming language

    • length of list

• measure speed of algorithm

  • better because it’s based on number of operations it requires to be carried out

how come the length of list (data) and algorithm is important factor of time complexity?

if we have a bubble sort for 5 numbers, it's efficient. If we have a bubble sort for 1 million numbers, it's not efficient.

therefore, the length of the list is an important factor.

how to calculate execution time in algorithms: BASIC RULES

number of times loops repeat relates to size of input, denoted by n

when statements are simply evaluated sequentially by computer, it takes constant amount of time to execute, denoted by k

• easy to count few instructions but when it becomes more complex we calculate time complexity using operation of algorithm

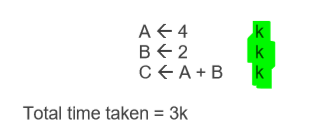
how to calculate execution time in algorithms: FOR LOOPS

For loop condition is executed n+1 times since it requires one extra check to see whether terminating condition has been satisfied

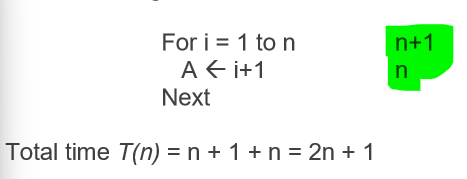
how to calculate execution time in algorithms: FOR LOOPS

execution times within inner FOR loop will be multiplied by those of outer loop. this produces a polynomial

Basic operation

operation contributing most total running time

asymptotic behaviour

idea that as amount of data changes, difference between two algorithms increases

in mathsy terms: behaviour of function f(n) for very large values of n

what is Big O notation

analysis of an time complexity considering worst-case scenario and provides notation for upper bound running of a function

state the functions & Big O notation for:

• linear

• polynomial

• exponential

• logarithmic

exponential:

• function: y = 2^x

• Big O notation: O (aⁿ) e.g. O (3ⁿ)

polynomial:

• function: y = 2x²

• Big O notation: O (n^a) e.g. O (n³)

linear:

• function: y = 2x

• Big O notation: O (n)

logarithmic:

• function: y = log₁₀ x

• Big O notation: O (log n)

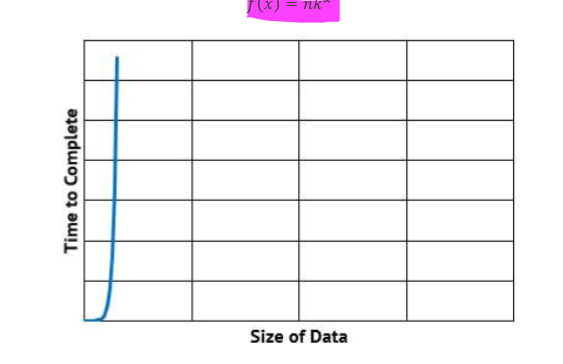
exponential time algorithms:

• take very long time to compute

• growth takes form K^x, where K is constant and x = 1,2,3….

• e.g. recursive Fibonacci numbers & recursive factorial calculations

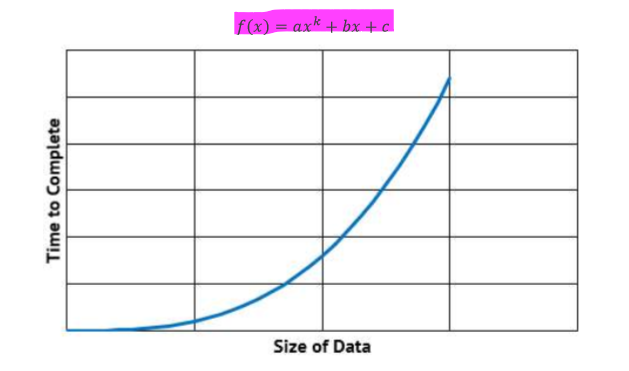
polynomial time algorithms

• mostly use nested loops

• growth has form x^k where K is a constant and x = 1,2,3…

• e.g. bubble and insertion sorts

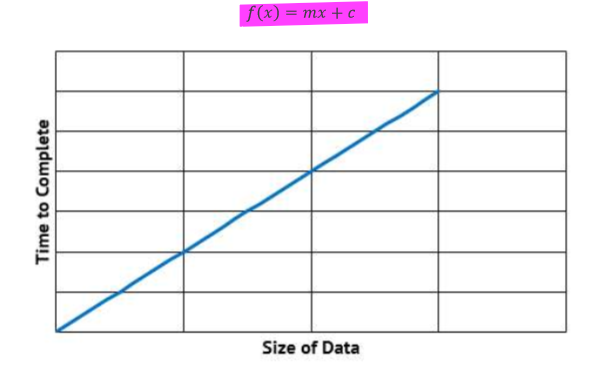
linear time algorithms

• go through data step by step

• growth has mx + c (← normal calculation for gradient of line we learnt in gcse math)

• e.g. linear search

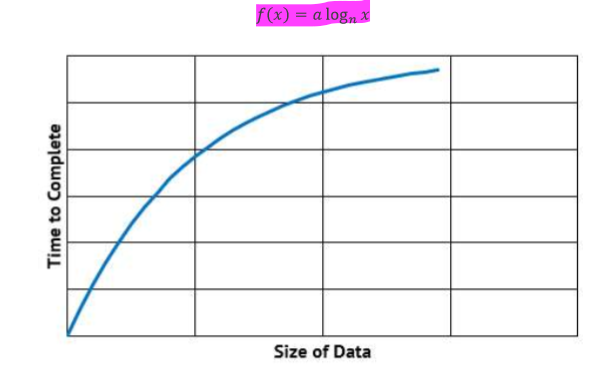
logarithmic time algorithms

• EXECUTION time does NOT increase as fast as IPUT size

• n is halved each cycle since log2 is used to see how many times we can multiply number by 2 until answer is reached

• e.g. binary search & binary tree search

constant time algorithm

• time complexity remains same regardless of number of inputs

• e.g. finding first item in list

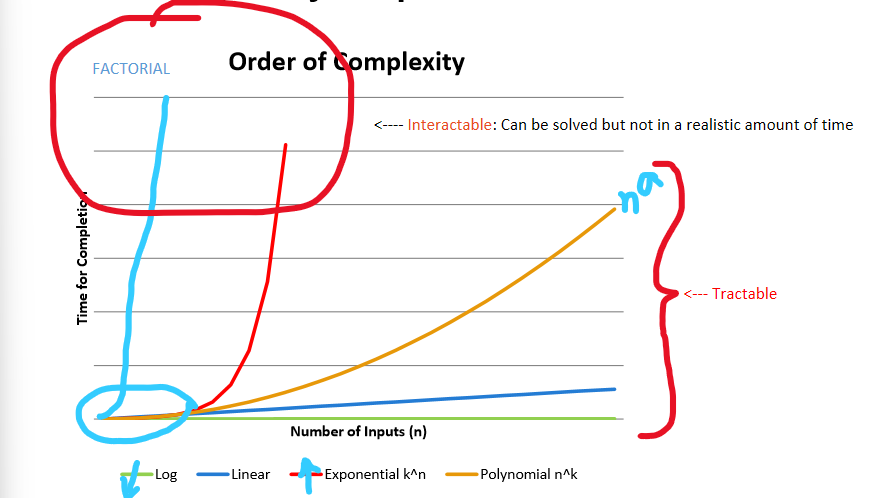
draw the order of complexity graph:

most time consuming/ worst case scenario

• factorial

• exponential

• polynomial

• linear

• logarithmic

least time consuming/ best case scenario

Big-O Rules:

how to express functions as Big-O

• only look at section that changes most significantly, make rest redundant

  • take off term from function which would give largest number

state the best/ave./wost case time complexity for searching algorithms

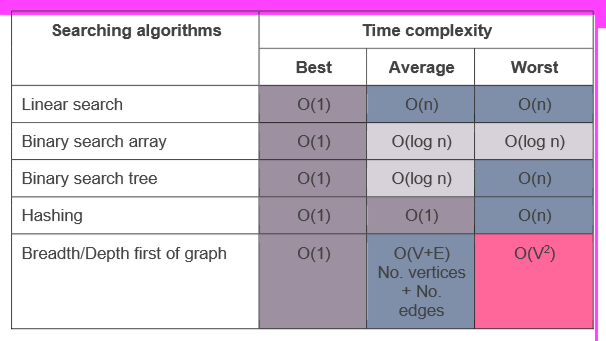
state the best/ave./wost case time complexity for sorting algorithms

define tractable problems + state an example

problem that can be solved in acceptable amount of time

• e.g. searching ordered list

define intractable problems + state an example

problems that can be solved but not in an acceptable time frame

• e.g. travelling salesman (has to travel between cities. distance between each pair of cities is known. he must visit each city once and return to start point. must calculate shortest route)

how are interactable problems tackled?

programmer produces heuristic algorithm

what are heuristic algorithms

method for producing a “rule of thumb“ to produce an acceptable solution to common sets of data and interactable programs within acceptable time frame

• unlikely to produce optimal results but can produce results which are satisfactory in acceptable time frame

computable problems

problems that have effective procedure/ algorithm to solve them. contain finite set of instructions

non computable problems

never be able to be solved using a computer, irrespective of processing power

e.g. halting problem