Chapter 9: Differential Equations
A. Basic Definitions
- A differential equation (d.e.) is any equation involving a derivative.
- A solution of a d.e. is any function that satisfies it. We see from (2) above that the d.e. (1) has an infinite number of solutions—one for each real value of C. We call the family of functions (2) the general solution of the d.e. (1). With the given initial condition x(0) = 3, we determined C, thus finding the unique solution (3).
- This is called the particular solution.
- Note that the particular solution must not only satisfy the differential equation and the initial condition, but the function must also be differentiable on an interval that contains the initial point.
- Features such as vertical tangents or asymptotes restrict the domain of the solution.
- Therefore, even when they are defined by the same algebraic representation, particular solutions with different initial points may have different domains. Determining the proper domain is an important part of finding the particular solution.
Rate of Change
A differential equation contains derivatives.
- A derivative gives information about the rate of change of a function.
Example:
- If P is the size of a population at time t, then we can interpret the d.e.
dP/dt=0.0325P
as saying that at any time t the rate at which the population is growing is proportional (3.25%) to its size at that time.
- The d.e. dQ/dt=−(0.000275)Q tells us that at any time t the rate at which the quantity Q is decreasing is proportional (0.0275%) to the quantity existing at that time.
- In psychology, one typical stimulus-response situation, known as logarithmic response, is that in which the response y changes at a rate inversely proportional to the strength of the stimulus x. This is expressed neatly by the differential equation
dy/dx=k/x (k is a constant
If we suppose, further, that there is no response when x = x0, then we have the condition y = 0 when x = x0.
- We are familiar with the d.e.
a=d^2s/dt^2=−32 ft/sec2
for the acceleration due to gravity acting on an object at a height s above ground level at time t. The acceleration is the rate of change of the object’s velocity.
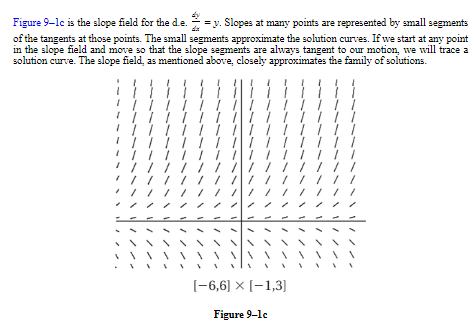
B. Slope Fields
- In this section we investigate differential equations by obtaining a slope field or calculator picture that approximates the general solution.
- We call the graph of a solution of a d.e. a solution curve.
- The slope field of a d.e. is based on the fact that the d.e. can be inter preted as a statement about the slopes of its solution curves.
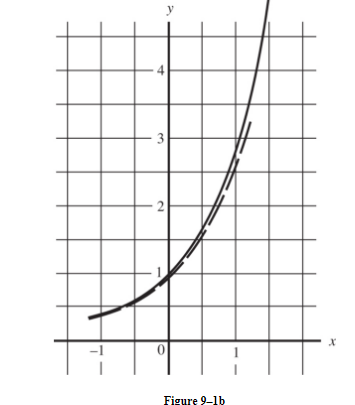
Example:
 \n
\n
 \n C. Euler’s Method
\n C. Euler’s Method
- When we use a slope field we start at an initial point, then move step by step so the slope segments are always tangent to the solution curve.
- With Euler’s method we again select a starting point; but now we calculate the slope at that point (from the given d.e.), use the initial point and that slope to locate a new point, use the new point and calculate the slope at it (again from the d.e.) to locate still another point, and so on.
Example 7
Given the d.e. dy/dx=x+y with initial condition y(0) = 0, use Euler’s method with Δx = 0.1 to estimate y when x = 0.5.
SOLUTION: Here are the relevant computations:
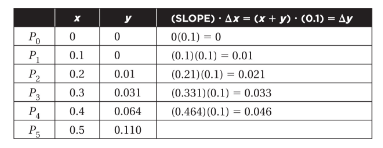
D. Solving First-Order Differential Equations Analytically
In the preceding sections we solved differential equations graphically, using slope fields, and numerically, using Euler’s method. Both methods yield approximations. In this section we review how to solve some differential equations exactly.
Separating Variables
A first-order d.e. in x and y is separable if it can be written so that all the terms involving y are on one side and all the terms involving x are on the other.
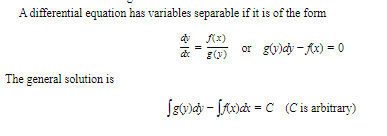
Example :
Solve the d.e. dy/dx=−xy, given the initial condition y(0) = 2.
SOLUTION:
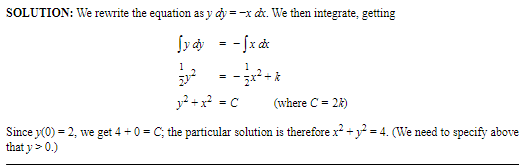
E. Exponential Growth and Decay
I. Exponential Growth
An interesting special differential equation with wide applications is defined by the following statement: “A positive quantity y increases (or decreases) at a rate that at any time t is proportional to the amount present.” It follows that the quantity y satisfies the d.e.
dy/dt=ky (1)
where k > 0 if y is increasing and k < 0 if y is decreasing.
From (1) it follows that
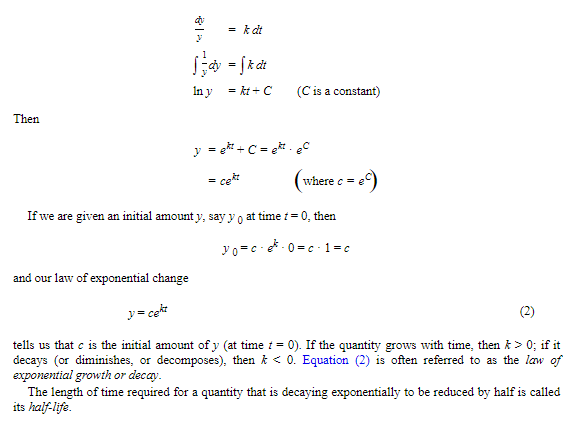
Example:
The population of a country is growing at a rate proportional to its population. If the growth rate per year is 4% of the current population, how long will it take for the population to double?
SOLUTION:
If the population at time t is P, then we are given that dP/dt=0.04 Substituting in equation (2), we see that the solution is
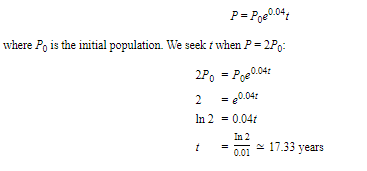
Applications of Exponential Growth
- A colony of bacteria may grow at a rate proportional to its size.
- Other populations, such as those of humans, rodents, or fruit flies, whose supply of food is unlimited may also grow at a rate proportional to the size of the population.
- Money invested at interest that is compounded continuously accumulates at a rate proportional to the amount present. The constant of proportionality is the interest rate.
- The demand for certain precious commodities (gas, oil, electricity, valuable metals) has been growing in recent decades at a rate proportional to the existing demand.
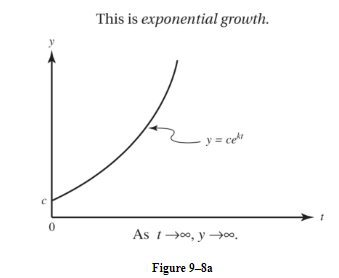
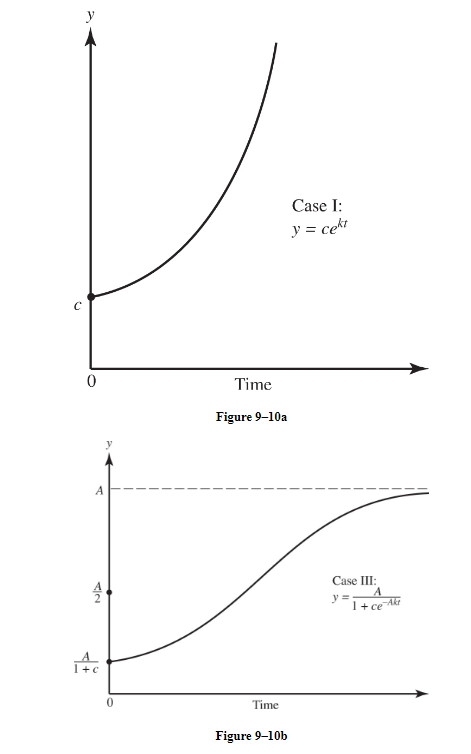
Each of the above quantities (population, amount, demand) is a function of the form cekt (with k > 0). (See Figure 9-8a.)
- Radioactive isotopes, such as uranium-235, strontium-90, iodine-131, and carbon-14, decay at a rate proportional to the amount still present.
- If P is the present value of a fixed sum of money A due t years from now, where the interest is compounded continuously, then P decreases at a rate proportional to the value of the investment.
- It is common for the concentration of a drug in the bloodstream to drop at a rate proportional to the existing concentration.
- As a beam of light passes through murky water or air, its intensity at any depth (or distance) decreases at a rate proportional to the intensity at that depth.
Each of the above four quantities (5 through 8) is a function of the form ce−kt (k > 0). (See Figure 9-8b.)
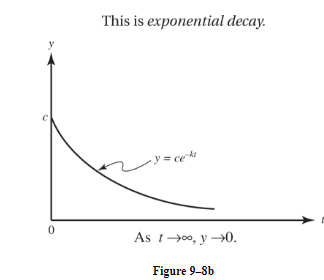
II. Restricted Growth
The rate of change of a quantity y = f(t) may be proportional, not to the amount present, but to a difference between that amount and a fixed constant. Two situations are to be distinguished: The rate of change is proportional to
(a)a fixed constant A minus the amount of the quantity present:
f′(t) = k [A − f(t)]
(b)the amount of the quantity present minus a fixed constant A:
f′(t) = −k [f(t) − A]
where (in both) f(t) is the amount at time t and k and A are both positive. We may conclude that
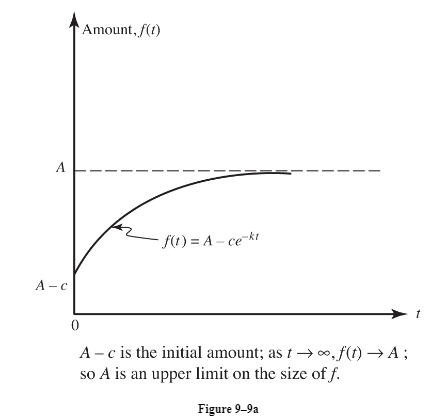
(a)f(t) is increasing (figure 9-9a):
f(t) = A − ce−kt
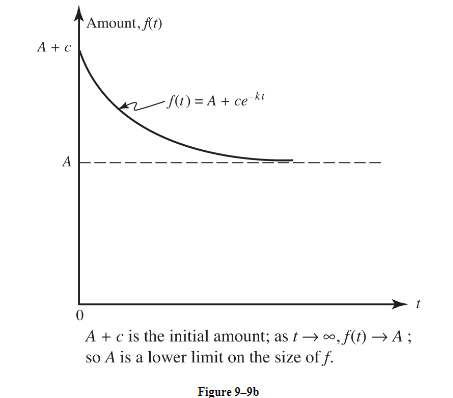
(b)f(t) is decreasing (figure 9-9b):
f(t) = A + ce−kt
for some positive constant c.
 \n Here is how we solve the d.e. for Case II(a), whereA − y > 0. If the quantity at time t is denoted by y and k is the positive constant of proportionality, then
\n Here is how we solve the d.e. for Case II(a), whereA − y > 0. If the quantity at time t is denoted by y and k is the positive constant of proportionality, then
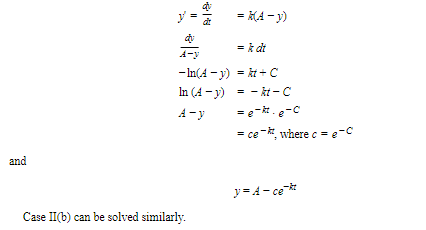
Example :
Advertisers generally assume that the rate at which people hear about a product is proportional to the number of people who have not yet heard about it. Suppose that the size of a community is 15,000, that to begin with no one has heard about a product, but that after 6 days 1500 people know about it. How long will it take for 2700 people to have heard of it?
SOLUTION:

Applications of Restricted Growth
(1) Newton’s law of heating says that a cold object warms up at a rate proportional to the difference between its temperature and that of its environment. If you put a roast at 68°F into an oven of 400°F, then the temperature at time t is R(t) = 400 − 332e−kt.
(2) Because of air friction, the velocity of a falling object approaches a limiting value L (rather than increasing without bound). The acceleration (rate of change of velocity) is proportional to the difference between the limiting velocity and the object’s velocity. If initial velocity is zero, then at time t the object’s velocity V(t) = L (1 − e−kt).
(3) If a tire has a small leak, then the air pressure inside drops at a rate proportional to the difference between the inside pressure and the fixed outside pressure O. At time t the inside pressure P(t) = O + ce−kt.
III. Logistic Growth
The rate of change of a quantity (for example, a population) may be proportional both to the amount (size) of the quantity and to the difference between a fixed constant A and its amount (size). If y = f(t) is the amount, then
| y′ = ky(A − y) | (1) |
|---|
where k and A are both positive. Equation (1) is called the logistic differential equation; it is used to model logistic growth.
The solution of the d.e. (1) is
| y=A/1+ce^−Akt | (2) |
|---|
for some positive constant c.
In most applications, c > 1. In these cases, the initial amount A/(1 + c) is less than A/2. In all applications, since the exponent of e in the expression for f(t) is negative for all positive t, therefore, as t → ∞,
(1)ce^−Akt → 0
(2)the denominator of f(t) → 1
(3)f(t) → A
Thus, A is an upper limit of f in this growth model. When applied to populations, A is called the carrying capacity or the maximum sustainable population.
Shortly we will solve specific examples of the logistic d.e. (1), instead of obtaining the general solution (2), since the latter is algebraically rather messy. (It is somewhat less complicated to verify that y′ in (1) can be obtained by taking the derivative of (2).)
Unrestricted Versus Restricted Growth
In Figure 9-10a and Figure 9-10b, we see the graphs of the growth functions of Cases I and III. The growth function of Case I is known as the unrestricted (or uninhibited or unchecked) model. It is not a very realistic one for most populations. It is clear, for example, that human populations cannot continue endlessly to grow exponentially. Not only is Earth’s land area fixed, but also there are limited supplies of food, energy, and other natural resources. The growth function in Case III allows for such factors, which serve to check growth. It is therefore referred to as the restricted (or inhibited) model.
- The two graphs are quite similar close to 0. This similarity implies that logistic growth is exponential at the start—a reasonable conclusion, since populations are small at the outset.
- The S-shaped curve in Case III is often called a logistic curve. It shows that the rate of growth y′:
(1)increases slowly for a while; i.e., y″ > 0
(2)attains a maximum when y = A/2, at half the upper limit to growth
(3)then decreases (y″ < 0), approaching 0 as y approaches its upper limit
It is not difficult to verify these statements.
Applications of Logistic Growth
Some diseases spread through a (finite) population P at a rate proportional to the number of people, N(t), infected by time t and the number, P − N(t), not yet infected. Thus N ′(t) = kN(P − N) and, for some positive c and k,
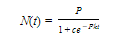
A rumor often spreads through a population P according to the formula in (1), where N(t) is the number of people who have heard the rumor and P − N(t) is the number who have not.
Bacteria in a culture on a Petri dish grow at a rate proportional to the product of the existing population and the difference between the maximum sustainable population and the existing population. (Replace bacteria on a Petri dish by fish in a small lake, ants confined to a small receptacle, fruit flies supplied with only a limited amount of food, yeast cells, and so on.)
Advertisers sometimes assume that sales of a particular product depend on the number of TV commercials for the product and that the rate of increase in sales is proportional both to the existing sales and to the additional sales conjectured as possible.
In an autocatalytic reaction a substance changes into a new one at a rate proportional to the product of the amount of the new substance present and the amount of the original substance still unchanged.
Example:
Suppose a flu-like virus is spreading through a population of 50,000 at a rate proportional both to the number of people already infected and to the number still uninfected. If 100 people were infected yesterday and 130 are infected today:
(a) write an expression for the number of people N(t) infected after t days
(b) determine how many will be infected a week from today
(c) indicate when the virus will be spreading the fastest
SOLUTIONS:
