Hashing

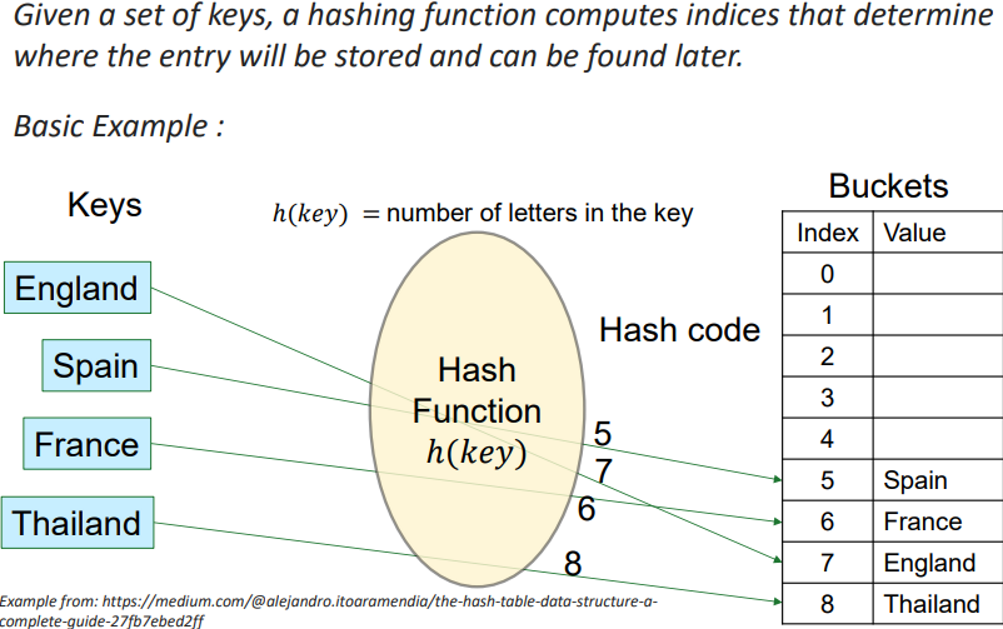
Hashing Function

Converts a key (often a string) to an integer

Integer is used for indexing a storage array

• The same deterministic function is used for storing and retrieving data

Index integer is not just restricted to 0 to 25

• Hence, data can be spread across a much longer array

How do we Deal with Collisions?

chaining

Hash Table

data structure that is designed to be fast to work with

Hash Function

takes the key of an element to generate a hash code

maps keys to array indices

Hash Code

says what bucket the element belongs to, so we can now find it assuming no collisions

Buckets

array indices

where the elements are stored

What is the Unique Part of an Element?

the key

How does Hashing Work? (diagram)

Increasing Range of Indexes

• For more objects (more keys), need longer array to minimise collisions

• Hashing function needs to produce a large range of integers

• Use more information from each key

  • e.g. all letters, and perhaps length

• But, just adding these together, a 15-letter key will rarely give an index, say, over 300

Designing a Good Hashing Function

• minimise collisions

• get a wide range of index values

Minimising Collisions

• a wide range of index values and

• unform hashing (each key is equally likely to map to an array location)

Getting a Wide Range of Index Values

use multiplication as well as addition

Dealing with Large Indices

If we want to use an array of length size, we can use: 

• index = rawIndex%size: 

where % is the integer remainder operation (modulo)

• e.g. to store 50 or so words, choose size = 100: 

  • key = "pace", rawIndex = 71671 

    • index = 71671%100 = 71 

  • key = "cart", rawIndex = 345438 

    • index = 345438%100 = 38

The Hashing Pitfall

Note that hash retrieval has two stages: 

1. Use hashing function to compute index

2. Search chain in array element to see if there is a match 

With a good hashing function and a large array, Stage 2 can be close to O(1), but, Stage 1 should also be fast

Real-World Hashing Functions…

• avoid slow multiplication and division operations 

• use fast logical shift and ‘OR’ operations

Multiplication vs Bit Shifting

• Multiplication is a slow operation

• Where the multiplier is a power of 2, we can left shift the bits in the multiplicand (X) by the power of 2 instead, and get exactly the same answer

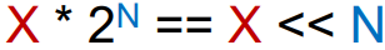
Why do we use Key-Value Pairs?

to distinguish between key-value pairs with the same hash

Key

unique input to hash function that is translated by hash function

Value

what we put in the bucket associated with the key

Hash Table ADT

• Stores key-value pairs

• Keys are unique and a handle to the associated value

• Operations

  • put(t, k) stores k in the table t

  • get(t, k) returns if k is in t else nil

  • delete(t, k) removes k from t

Hash Table ADT Pseudocode

//chains are lists; A is hash table array

put(t, <k,v>) {
	chain = t.A[hash(k)]
	//C doesn't have to be sorted
	add(chain, <k,v>)
}

get(t, k) {
	chain = t.A[hash(k)]
	return search(chain,k)
}

delete(t, k) {
	chain = t.A[hash(k)]
	remove(chain,k)
}

What Happens if Chains Grow too Long

• Hash tables become less efficient

Avoiding Chains Growing too Long

hash table allocates double the size of current array

then puts each in current array into larger array

expensive operation

invisible to the user of the ADT