3.1 Derivatives of Polynomials and Exponential Functions

In this section we learn how to differentiate constant functions, power functions, polyno- mials, and exponential functions.

What is the derivative of a Constant Function ?

The derivative of a constant function is always zero because a constant function has a constant value, meaning its rate of change is zero.

Derivative of a constant Function

A formal proof, from the definition of a derivative, is also easy:

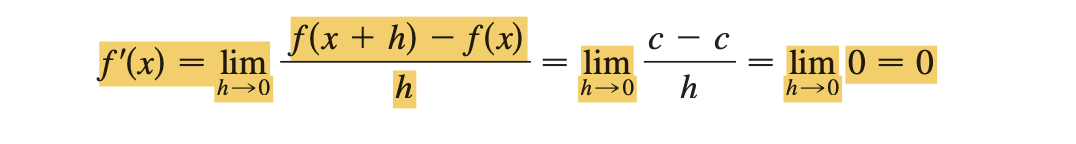
Definition of a Constant Function in Leibniz notation:

Power Functions 

We look at the functions F(x) =x^n, where n is a positive integer. 

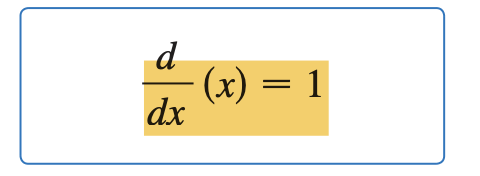
The Power Rule 

This is a shortcut for finding the derivative of a variable raised to a power. 

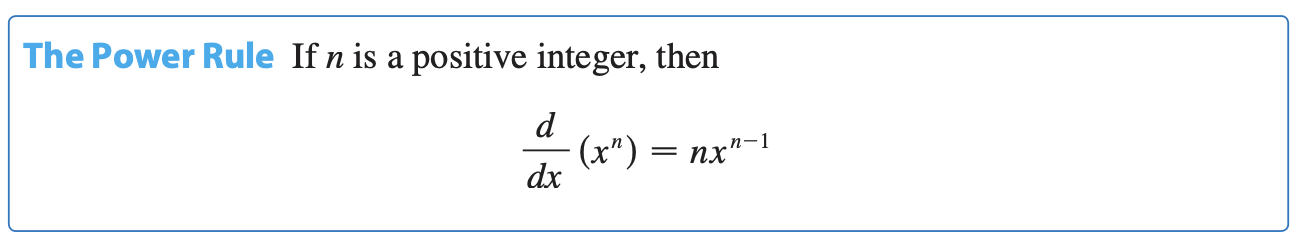
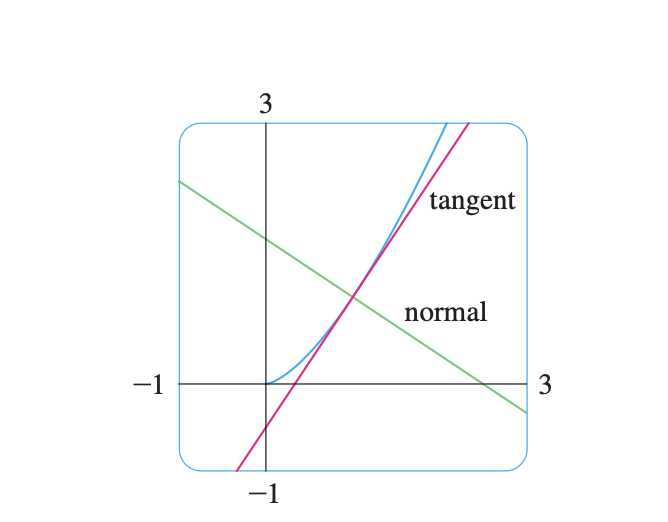
How does the Power Rule enable us to find tangent lines without having to resort to the definition derivative? 

It also enables us to find normal lines. The normal line to a curve

C at a point P is the line through P that is perpendicular to the tangent line at P.

New Derivatives from Old

When new functions are formed from old functions by addition, subtraction, or multiplication by a constant, their derivatives can be calculated in terms of derivatives of the old

functions.

The Constant Multiple Rule

If c is a constant and f is a differentiable function, then the derivative of a constant times a function is the constant times the derivative of the function.

The Sum Rule

The next rule tells us that the derivative of a sum of functions is the sum of the

derivatives.

The Difference Rule 

By writing f- g as f + (-1)g  and applying the Sum Rule and the Constant Multiple

Rule, we get the following formula.

Horizontal Tangents Derivative 

Horizontal tangents occur where the derivative is zero.

What is an Exponential Function?

An exponential function is a mathematical function where a constant base is raised to a variable exponent.

Definition of the Number e

f(x)= e^x

Geometrically, this means that of all the possible exponential functions y b^ x, the

function f (x) = e^x is the one whose tangent line at (0, 1) has a slope f’(0) that is exactly

1.

Derivative of the Natural Exponential Function

This exponential Function has the property that it is it’s own derivative.

The geometrical significance of this fact is that the slope of a tangent line to the curve y=e^x is equal to the y-coordinate of the point.