CH 4 Derivatives (DONE)
1/31
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
32 Terms
Consumption vs Investment Assets
Investment assets are assets held by significant numbers of people purely for investment purposes (Examples: gold, silver)
Consumption assets are assets held primarily for consumption (Examples: copper, oil)
Short Selling
Short selling involves selling securities you do not own
Your broker borrows the securities from another client and sells them in the market in the usual way
Short Selling (continued)
At some stage you must buy the securities so they can be replaced in the account of the client
You must pay dividends and other benefits the owner of the securities receives
There may be a small fee for borrowing the securities
You short 100 shares when the price is $100 and close out the short position three months later when the price is $90
During the three months a dividend of $3 per share is paid
What is your profit?
What would be your loss if you had bought 100 shares?
Profit = $100 per share - $90 per share = $10 - $3 dividend = $7 profit
Bought 100 shares: $90 - $100 = -$10 + $3 dividend = -$7 loss
Notation for Valuing Futures and Forward Contracts

Suppose that:
The spot price of a non-dividend-paying stock is $40
The 3-month forward price is $43
The 3-month US$ interest rate is 5% per annum
Is there an arbitrage opportunity?
*(Good Example)*
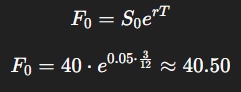
Compare prices:
Market forward = $43
Fair forward = $40.50
Since $43 > $40.50, the forward is overpriced → arbitrage exists
Arbitrage strategy:
Borrow $40 at 5%
Buy the stock
Sell (short) the forward at $43
Profit at maturity:
43 - 40.50 = 2.50
Buy the Stock, Sell the Forward
Suppose that:
The spot price of non-dividend-paying stock is $40
The 3-month forward price is US $39
The 1-year US$ interest rate is 5% per annum (continuously compounded)
Is there an arbitrage opportunity?
*(Good Example)*
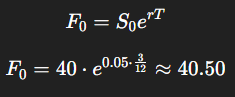
Compare prices:
Market forward = $39
Fair forward = $40.50
Since $39 < $40.50, the forward is underpriced → arbitrage exists
Arbitrage strategy:
Short sell the stock at $40
Invest $40 at 5%
Buy (go long) the forward at $39
Profit at maturity:
40.50 − 39 = 1.50
Short the Stock, Buy the Forward
If the spot price of an investment asset that provides no income is S0 and the futures price for a contract deliverable in T years is F0, then
F0 = S0erT
where r is the T-year risk-free rate of interest.
In our examples, S0 =40, T=0.25, and r=0.05 so that
F0 = 40e0.05×0.25 = 40.50
If Short Sales Are Not Possible..
Formula still works for an investment asset because investors who hold the asset will sell it and buy forward contracts when the forward price is too low
When an Investment Asset Provides a Known Income (equation 5.2)

When an Investment Asset Provides a Known Yield (equation 5.3)
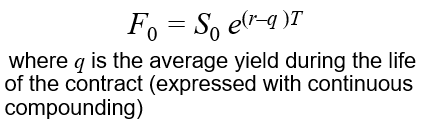
Valuing a Forward Contract
A forward contract is worth zero (except for bid-offer spread effects) when it is first negotiated
Later it may have a positive or negative value
Suppose that K is the delivery price and F0 is the forward price for a contract that would be negotiated today
By considering the difference between a contract with delivery price K and a contract with delivery price F0 we can deduce that:
the value of a long forward contract is
(F0 – K )e–rT
the value of a short forward contract is
(K – F0 )e–rT
Forward vs Futures Prices
When the maturity and asset price are the same, forward and futures prices are usually assumed to be equal. (Eurodollar futures are an exception)
In theory, when interest rates are uncertain, they are slightly different:
A strong positive correlation between interest rates and the asset price implies the futures price is slightly higher than the forward price
A strong negative correlation implies the reverse
Stock Index (equation 5.8)
Can be viewed as an investment asset paying a dividend yield
The futures price and spot price relationship is therefore
F0 = S0 e(r–q )T
where q is the average dividend yield on the portfolio represented by the index during life of contract
Stock Index (continued)
For the formula to be true it is important that the index represent an investment asset
In other words, changes in the index must correspond to changes in the value of a tradable portfolio
The Nikkei index viewed as a dollar number does not represent an investment asset (See Business Snapshot 5.3)
Index Arbitrage
When F0 > S0e(r-q)T an arbitrageur buys the stocks underlying the index and sells futures
When F0 < S0e(r-q)T an arbitrageur buys futures and shorts or sells the stocks underlying the index
Index Arbitrage
(continued)
Index arbitrage involves simultaneous trades in futures and many different stocks
Very often a computer is used to generate the trades
Occasionally simultaneous trades are not possible and the theoretical no-arbitrage relationship between F0 and S0 does not hold (see Business Snapshot 5.4)
Futures and Forwards on Currencies (equation 5.9)
A foreign currency is analogous to a security providing a yield
The yield is the foreign risk-free interest rate
It follows that if rf is the foreign risk-free interest rate
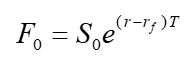
Explanation of the Relationship Between Spot and Forward (Figure 5.1)
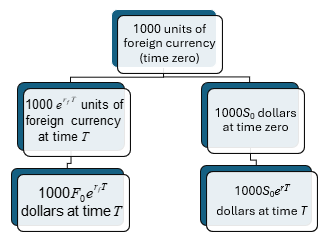
Consumption Assets: Storage is Negative Income (equations 5.11 and 5.12)
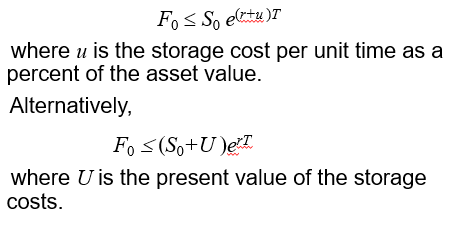
The Cost of Carry (equation 5.19)
The cost of carry, c, is the storage cost plus the interest costs less the income earned
For an investment asset F0 = S0ecT
For a consumption asset F0 ≤ S0ecT
The convenience yield on the consumption asset, y, is defined so that F0 = S0 e(c–y )T
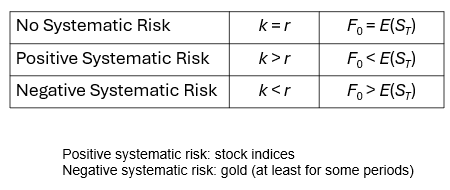
Futures Prices & Expected Future Spot Prices (equation 5.20)
Suppose k is the expected return required by investors in an asset
We can invest F0e–r T at the risk-free rate and enter into a long futures contract to create a cash inflow of ST at maturity
This shows that
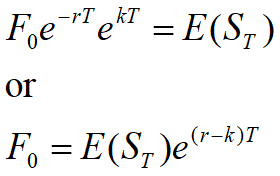
Futures Prices & Future Spot Prices (continued)
Price Forecasting
A large number of factors drive the price of any given futures contract. Chief among these factors is the price of the underlying cash commodity or financial instrument.
As the price of the underlying commodity or instrument changes, the price of the futures contract will change.
The price of the futures contract has a direct correlation to the price of the underlying commodity or instrument upon which the contract is based.
The relationship between the price of the futures contract and the price of the underlying commodity or instrument is kept in a tight range, as the forces of an efficient market continually monitor the relationship.
Sophisticated traders and funds are constantly running the prices of the cash and futures markets through advanced pricing models, seeking out opportunities that result from pricing inefficiencies.
Futures Market Pricing Structure
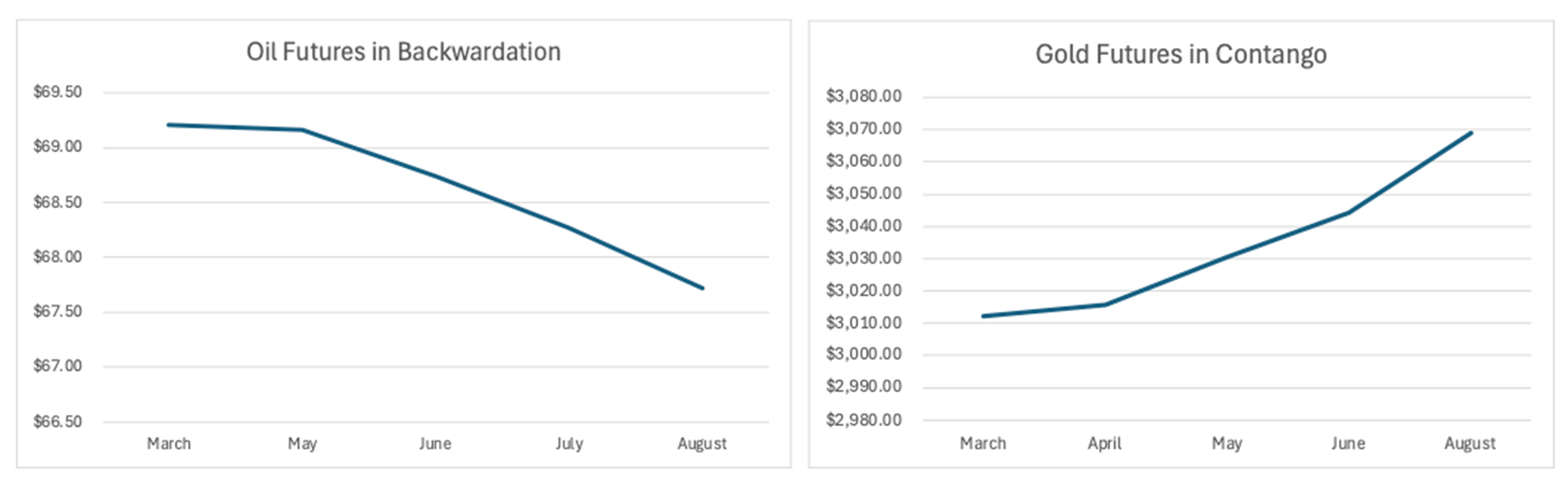
The pricing structure of the futures market in relationship to the physical cash commodity in normal market conditions is upward sloping. That is to say that the price of the futures trades above the price of the cash commodity and that futures contracts have successively higher prices the further the delivery date extends.
A market that has distant contract months trading at prices higher than near-term contract months is said to be contango, a premium market, a carrying charge market, or a normal market.
The price of the cash commodity and near and distant futures contracts will all tend to move in the same direction. If the price of the underlying commodity rises, the price of the near and distant futures contracts will rise. The opposite is true when the price of the underlying commodity falls.
As the delivery month approaches, the price of the cash commodity and spot futures contract will converge, effectively pricing the contract during the delivery period as if it was equal to the cash commodity.
A market that has distant contract months trading at prices higher than near-term contract months is said to be __________, a premium market, a carrying charge market, or a normal market.
contango
Futures Market Pricing Structure
Contango is when the futures price of an asset is higher than its current (spot) price. Backwardation is the opposite, when the current price is higher than the asset’s futures price.
Contango is considered a normal market condition because assets generally rise in value over time, and physical commodities have carrying costs.
Contango can also tell us that the market is bullish. When the spot price is lower than that in the future, investors expect the asset to be worth more as time passes, which is what is seen in most markets. This also indicates confidence in economic growth and favorable future supply-demand dynamics, the main driver of commodity prices.
________ is when the futures price of an asset is higher than its current (spot) price. ________________ is the opposite, when the current price is higher than the asset’s futures price.
Contango | Backwardation
However, different markets are affected by various different factors. Mainly, contango is caused by the following:
Carrying costs
Inflation
Supply/demand disruptions
Market uncertainty and sentiment
Over time, futures prices converge with the spot price as their contract expiration date gets closer. As the expiry date draws closer, the price is more reflective of the actual value of the commodity. The closer the delivery date, the smaller the window for a drastic change in price.
Backwardation can occur if the market foresees prices falling and in markets that experience seasonal changes in supply and demand.
Contango vs Backwardation of Commodities