MMW Flashcards

Patterns

foundation of mathematics and are present all around us. They give us the ability to discover new ideas, make predictions, and even influence the future.

Patterns of Visuals

often unpredictable, never quite repeatable, and often contain fractals, appealing to the eyes.

Patterns of Flow

flow of liquids, sense of direction, repeatable, recurring.

Patterns of Movement

regular rhythm just like the walk of humans; left right left right rhythm

Patterns of Rhythm

uses beat and is the most basic pattern in nature

Patterns of Texture

uses the sense of touch; literal surface that we can feel, see, and imagine.

Geometric Patterns

consists of a series of shapes/tiles that are typically repeated.

Reflection Symmetry

when the left half of a pattern is the same as the right half.

Line Symmetry or Mirror Symmetry

Other terms for reflection symmetry

Rotational Symmetry

captures symmetries when it still looks the same after some rotation of less than one full turn.

Translational Symmetry

exists in patterns that we see in nature and in man-made objects. Translations acquire symmetries when units are repeated and turn out having identical figures

Fibonacci

numbers appear throughout nature, from the smallest to the largest forms.

Sequence

refers to an ordered list of numbers called terms, that may have repeated values. The arrangement of these terms is set by a definite rule.

Arithmetic Sequence

A sequence that follows a definite pattern; pattern that uses a common difference

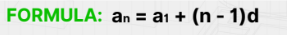
Formula for Arithmetic Sequence

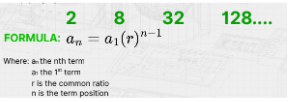
Formula for Geometric Sequence

Geometric Sequence

A sequence of numbers that follows a pattern where the next term is found by multiplying a constant called the common ratio.

Harmonic Sequence

The reciprocal of the terms behave like arithmetic sequence.

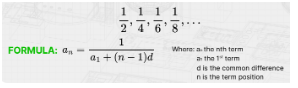
formula for Harmonic Sequence

Fibonacci Sequence

is an integer in the infinite sequence 1,1, 2, 3, 5, 8, 13,.. of which the first two terms are 1 and 1 and each succeeding term is the sum of the two immediately preceding.

1.618

What is the value of the golden ratio?

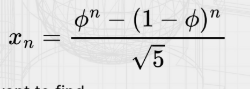
What is the formula of Fibonacci Sequence?

Precise, Concise, Powerful

Characteristics of a mathematical language

What symbol is a connective?

+/ plus sign

Expression

mathematical equivalent of an english noun

N sub 0

natural numbers / whole numbers set with zero

N sub 1

natural numbers / whole numbers set without zero

Z

integer numbers set

Q

rational numbers set

R

real numbers set. all rational or irrational numbers mostly are decimal.

C

complex number set, usually in the form a+bi

Unit set

set that contains only one element

Empty set

set that has no element

Finite set

set that the elements in a given set is countable

Infinite set

set that elements has no end or not countable

Cardinal Number

denoted by n; used to measure the number of elements in a given set.

Equal set

said to be equal if both cardinality and the elements are identical

Equivalent set

exact number of element or same cardinal numbers ; 1 to 1 correspendonce

Universal set

set of all elements under discussion

Joint sets

said to be blank if and only if they have common element/s

Disjoint sets

if and only if they are mutually exclusive or if they don’t have common element/s

Roster or tabular method

method of describing a set; done by listing or tabulating the elements of the set

Rule or set-builder method

stating or describing the common characteristics of the elements of the set. a {x|x…}

Proof

rigorous mathematical argument which unequivocally demonstrate the truth of a given proposition.

Proposition

declarative statement that is true or false but not both.

corollary

proposition that follows with little or no proof required from one already proven

Lemma

Lemma short theorem used in proving a larger theorem

Conjecture

conclusion drawn from inductive reasoning; a proposition which is consistent with known data, but has neither been verified nor shown to be false. synonymous to hypothesis also known as an educated guess

Inductive Reasoning

drawing a general conclusion from a repeated observation or limited sets of observation of specific examples.

counterexample

proves the conjecture to be false.

deductive reasoning

drawing general to specific examples or simply from general case to specific case; starts with a general statement or hypothesis and examines to reach a specific conclusion.

Intuition

reliable mathematical belief without being formalized and be proven directly and serves as an essential part of mathematics.

Proof

inferential argument for a mathematical statement

Direct Proof

a mathematical argument that uses rules of inference to derive the conclusion from the premises. if p then q.

Indirect proof

or contrapositive proof; type of proof in which a statement to be proved is assumed false

Proof by counterexample

disproving universal statements

Proof by contradiction

assuming your implication is not true, then deriving a contradiction.