MMW FIRST SEM

PRELIMS

PATTERNS

are regular, repeated or recurring visual forms or designs.

ALAN TURNING

is the first to explain patterns of animals.

CRISTOBAL VILA

made a video about “Nature’s Number”

IAN STEWART

made a book about “Nature’s Numbers”

SYMMETRY

indicates that you can draw an imaginary line across an object and the resulting parts are mirror images of each other.

REFLECTION OR LINE

means on half of image is mirror image of the other half.

ROTATIONAL

means that when you rotate an object by specified measures of degrees.

ANGLE OF ROTATION

smallest angle that a figure can be rotated and still preserving the original formation. 360/n

BILATERAL

one plane divide into 2 mirror images

PENTARADIAL

Five planes divided the organism evenly.

RADIAL

more than 2 planes are divided into identical pieces.

SPHERICAL

the ability to draw an endless, or great but finite, number of symmetrical axes through the body.

FRACTALS

A never-ending pattern that are infinitely complex.

BENOIT MANDELBROT

“Father of Fractals”

SPIRALS

curve formed by point revolving around a fixed axis an ever-increasing distance.

MEANDERS

a series of regular sinuous curves, bends and loops, turns or windings in channel of river stream or another watercourse.

TESSELLATIONS

pattern made of identical shapes that fit together with no gaps and do not overlap.

APPLIED MATHEMATICS

deals with real - world problems and phenomena and try to model them by equations and formulas.

PURE MATHEMATICS

deals with abstract entities and tries to find relations between them and patterns and structures for them and generalize when possible.

SEQUENCE

is an ordered list of numbers.

TERM

refers to each number in a sequence.

NTH TERM FORMULA OF A SEQUENCE

A_n = 3n² + n

A_n = a₁ + (n —1) d

FIBONACCI SEQUENCE

series of numbers such that the next number is found by adding up two numbers before it.

F

is term number "n”

F_(n-1)

is the previous term (n-1)

F_(n-2)

is the term before that (n-2)

LEONARDO BIGOLLO PISANO/ LEONARDO BONACCI

known as “Fibonacci” an itallian mathematician.

FIBONACCI NUMBER GENERAL FORMULA

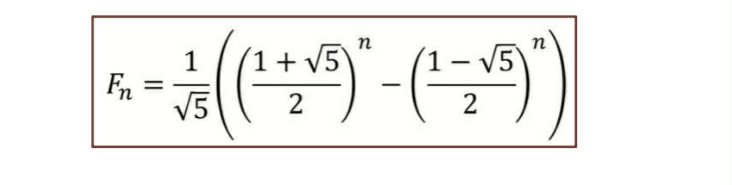
GOLDEN RATIO

based on Divine Proportion, the measurements of the Divine Proportion will look aesthetically pleasing.

GEOMETRY

fundamental science of forms and their order. It ensures the right proportions or using the golden ratio produces a well balanced furniture design.

GEOMETIRC FIGURES

forms and transformation build the material of architectural design.

GEOMTERIC PATTERNS

combine different shapes whether a repeated or altered to create a cohesive design.

ISOMETRY

in two parts Iso means same and metry means meter or measure, it is a transformation without a change  to a figure’s shape or size.

TRANSFORMATION

means change

TRANSLATION

move a shape in each direction by sliding it up, down, sideways or diagonally.

REFLECTION

without changing shape and size by flipping it along the reflection line creating a mirror image of it.

ROTATION

rotated about a fixed point (center of rotation) through a given angle.

DILATION

resized by scale factor about point

ROSSETE PATTERNS

consist of taking a motif or an element and rotating and/or reflecting that element.

FRIEZE PATTERNS

infinitely long strip imprinted with a design given by a repeating pattern motif.

WALLPAPER PATTERNS

covers the plane and can be mapped onto itself by translation in more than one direction.

TESSELLATIONS PATTERNS

when we cover a surface with pattern of flat shapes fitted together so that there are no overlaps or gaps.

M.C. ESCHER

famous tessellation artist Netherlands.

CHARACTERISTICS OF LANGUAGE OF MATHEMATICS

precise, concise, powerful.

IF ITS A NOUN/ SIMPLE EXPRESSION

• Cavite, Book

• 28, 4+3, 5>4

SENTENCE

• DLSU-D is a prime University

• x+y = z

CARDINAL

to express quantity

ORDINAL

to indicate order

NOMINAL

a label

GENERAL FERDINAND LUDWIG

was German mathematician. He created set theory.

SET

a well-defined collection of distinct objects.

LISTING

it has a curly brackets, Elements and Comma on repeat.

repea

SET BUILDER

Set of, All, such that, X less than four, Belongs to, Natural Numbers.

Na

VENN DIAGRAM

shows all possible logical relationships between a finite collection of different sets.

COMPLEMENT (n’)

subtracting the elements set from union, if the universal set is the numbers 1 through 8 and set A is the even numbers (2, 4, 6, 8), then the blank would be the odd numbers (1, 3, 5, 7). 

INTERSECTION (⋂)

similar element in both set combined, The intersection of two sets, A and B, is the set of all elements that belong to both A and B.
In set-builder notation, this is written as: A ∩ B = {x | x ∈ A and x ∈ B} 

Example 1:

• Set A = {2, 4, 6, 8} 

• Set B = {4, 8, 12, 16, 20} 

• A ∩ B = {4, 8} (because 4 and 8 are in both sets) 

UNION (⋃)

combination of all similar elements from both sets, a fundamental set operation that creates a new set containing all elements from two or more original sets, combining them into a single set. if set A is {1, 2, 3} and set B is {3, 4, 5}, then the union of A and B (A ∪ B) is {1, 2, 3, 4, 5}, with the common element '3' appearing only once. 

CARDINAL NUMBER

refers to number of elements in a set.

EQUIVALENT SETS

Set that has the same cardinal number regardless of its same elements.

regardless of its element.

EQUAL SETS

Precisely the same elements

NULL SETS (Ø)

no elements

N (NATURAL NUMBERS)

the counting numbers, meaning they are the positive integers 1, 2, 3, and so on, extending infinitely

W (WHOLE NUMBERS)

the non-negative integers {0, 1, 2, 3, ...}, including zero and all positive counting numbers.

Z (INTEGERS)

a number that can be written without a fractional or decimal component, meaning it is a whole number that can be positive, negative, or zero.

Q (RATIONAL)

any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers and 'q' is not zero, ncludes all whole numbers, integers, fractions, terminating decimals (like 0.5), and repeating decimals (like 0.333...).

Q’ IRRATIONAL

When written as decimals, they go on forever without a repeating pattern or a terminating point. 

R (REAL NUMBERS)

any numbers that can be found on a number line, and they encompass all rational numbers (integers, fractions, terminating decimals) and all irrational numbers (non-terminating, non-repeating decimals).

C (COMPLEX NUMBERS)

an extension of real numbers, written as a + bi, where 'a' is the real part, 'b' is the imaginary part, and 'i' is the imaginary unit defined as the square root of -1 (i² = -1).

⊂

subset

⊃

superset

NAUTILUS SHELL

the film Nature by Numbers, sea shell was used in the film to show the concept of Fibonacci spiral and golden ratio.

CRISTOBAL VILA

created the film" Nature by Numbers"

LOGICAL STATEMENT

a declarative sentence which conveys factual information. If the information is correct then we say the statement is true; and if the information is incorrect, then we say the statement is false

PROPOSITION

a statement that is either true or false (usually a declarative sentence.

SIMPLE STATEMENT

logical statement carrying one piece of information.

TRUTH VALUE

value indicating whether the proposition is known to be true / false, unknown, or a matter of opinion

UNIVERSALLY QUANTIFIED

If a logical statement applies to all objects in a collection. If every object in the collection fits the description, then the ——— statement is true

For example,

(1) Every McDonald’s serves french fries.

(2) All math majors study calculus.

EXISTENTIALLY QUANTIFIED

A logical statement which applies to some objects in a collection, _________ statement accurately describes at least one object in the collection, then it is true.

For example,

(1) Some people attend college.

(2) There are people who believe in UFO’s.

COMPOUND PROPOSITION

a complex logical statement formed by combining two or more simpler, atomic propositions using logical connectives such as "and," "or," "if...then," "not," or "if and only if"

LOGICAL OPERATIONS

combines propositions using a particular composition rule

TRUTH TABLE FOR COMPOUND PREPOSITION

If a compound proposition has n variables, there are 2^n rows

1. To fill in variable column, start with right-most variable column and fill in

alternation T and F pattern

2. Next column to the left, is filled by alternation TT and FF pattern

3. Next column to the left is filled in by alternating TTTT and FFFF pattern

4. For each new column to the left, the number of T’s and F’s in the pattern is

doubled

NEGATION

a new logical statement which says the opposite of the original statement. denoted by “¬”, reverses truth value of the proposition 

CONJUNCTION (^)

denoted by “∧”, similar to “AND” in boolean logic

DISCONJUNCTION (v)

denoted by “∨”, similar to “OR” in boolean logi

CONDITIONAL OR IMPLICATION (if - then, —>)

denoted by “→” (p→q reads as “if p then q”)

- proposition is false if p is true and q is false, otherwise p → q is true

- p is called the hypothesis, and the proposition q is called the conclusion

- Broken down it is ¬p v q

CONVERSE

If the original statement is in the form "If P, then Q," the converse statement is "If Q, then P".

CONTRAPOSITIVE

formed by swapping the hypothesis and conclusion of a conditional statement AND negating both. For a statement "If P, then Q" (P → Q), its contrapositive is "If not Q, then not P" (¬Q → ¬P).

INVERSE

formed from a conditional statement by negating both the hypothesis and the conclusion, while keeping the original order of the parts. If a conditional statement is "If P, then Q" (P → Q), then its ——— statement is "If not P, then not Q" (¬P → ¬Q). 

BICONDITIONAL (if and only if, <—→)

denoted as “p ↔ q” or “p if q”, read as “p if and only if q”

- Proposition p ↔ q is true when p and q have the same truth value, and false when p and q

have different truth values

- Order of operations if no parentheses:

1. ¬, ∧, and ∨

2. → or

DE MORGANS LAW

logical equivalences that show how to correctly distribute a negation

operation inside a parenthesize expression

1. ¬(p ∨ q) ≡ (¬p ∧ ¬q

LOGICALLY EQUIVALENT

Two compound propositions are said to be …………… if they have the same truth value

in individual cases

CONTRADICTION

A compound proposition is a ……….. if the proposition is always false, regardless how many cases

TAUTOLOGY

A compound proposition is a ……….. if the proposition is always true, regardless how many cases

LAWS OF PROPOSITIONAL LOGIC

If two propositions are logically equivalent, then one can be substituted for the other within a more complex proposition