Nuclear and Electronic Structure, Atoms and the Periodic Table

Equation for speed of light

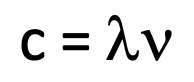
speed of light = wavelength x frequency

Energy of a photon

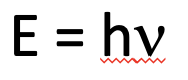
energy = planck’s constant x frequency of the light

Mass Defect

The atomic mass of every atom except hydrogen is less than the sum of the masses of protons. neutrons and electrons present.

A measure of the binding energy of the nucleus

How to calculate mass defect

the difference between the expected mass based on the number of protons, neutrons, and electrons and the observed mass of an atom

Binding energy

the energy released if all the protons, neutrons, and electrons were brought together

Equation to calculate energy equivalent to mass defect

E=mc² (mass defect=m)

What is considered a large amount of energy?

Hydrogen bonds (weak) - 15 kJ/mol

C-C bond - 350 kJ/mol

Burning 1 mole of butane - 2.86x10³ (large)

3 types of ionizing radiation

⍺, β, 𝛾

⍺ - radiation

A helium nucleus (atomic mass 4, atomic number 2 — 2 protons, 2 neutrons)

change in mass defect after alpha emissionn

β - radiation and emission

an electron

beta emission is the loss of an electron, mass number is almost unchanged, atomic number goes up by one - neutron changes to proton and gives out electron

Gamma radiation/emission

gamma radiation is electromagnetic radiation

it is emitted along with or after one of the other kinds of radiation when the new nucleus formed is in an excited state

gamma ray (hv)

excited/ high energy nucleus state is metastable, denoted by m

Nucleosynthesis

the process of making elements ( in the stars)

Big bang nucleosynthesis

hydrogen and helium were formed within the first few minutes of the start of the universe

big bang produced ¹H, ²H (D), ³H, ³He, ⁴He and a small amount of ⁷Li.

the mechanism of the process is the fusion of protons and neutrons with themselves and with small nuclei

Stellar nucleosynthesis

heavier elements are made from hydrogen and helium in stars using the process of nuclear fusion —when two or more nuclei react to form one or more different atom

processes depend on temperature and mass of stars — older and larger stars can produce heavier elements up to iron with the triple alpha process and the alpha ladder where helium nuclei (alpha particles) fuse with eachother and with the heavier nuclei that they form

Supernova nucleosynthesis

A supernova creates a lot of energy, necessary to create elements heavier than iron

Interference (2 types)

Constructive: two waves in phase interfere and add to give a greater amplitude

Destructive: two waves out of phase interfere and cancel out to give reduced or zero amplitude

How to find energy of a mole of photons

multiply energy for one photon times avogadro’s number

The photoelectric effect

UV radiation is directed onto a metal surface and electrons will be ejected from the surface of the material if the frequency of the UV radiation is above a threshold value

Electron must have at least a certain energy (workfunction)

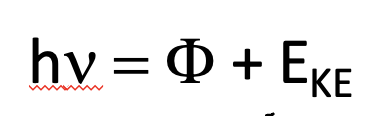
where E_KE is the kinetic energy of the ehected photoelectron

Bohr’s quantized model equation

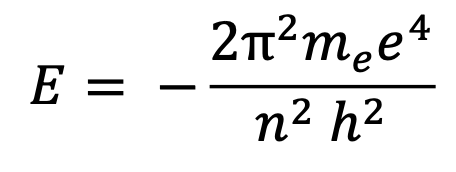
n is the principal quantum number— everything else is constant (m_e= mass of an electron; h= planck’s constant; e is the charge on the electron; pi)

The Bohr Atom

Electrons can only have particular quantized energies represented by the circular orbits

Quantization

Only certain energies are allowed, there are no “in between” energies (like a ladder)

possible energies labeled using letter n (principal quantum number)

Atomic spectrum of hydrogen

emission spectrum will have a line at hv = E₂ - E₁

The Rydberg equation

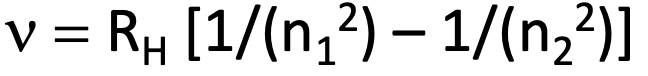
n is an integer used to number the energy levels

R_H is the Rydberg constant •= 3.29 x 10¹⁵ Hz (but different on data card, in m^-1

Main series to know

Lyman Series - n₁ = 1 (emissions start in excited state and emit until at n=1)

Balmer Series - n₁ = 2

Paschen Series - n₁ = 3

Ionization energies

if n₁ = 1 and n₂ = infinity then you get the ionization frequency which can be converted to ionization energy

limitations of Bohr model

It is very simple and doesn’t fit atoms bigger than hydrogen very well

The de Broglie equation

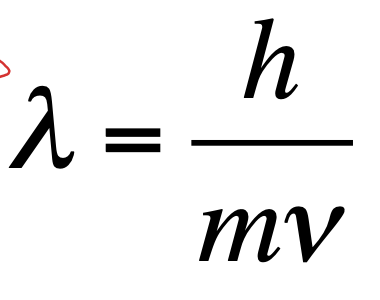
Waves can act like particles and particles can act like waves

•m = mass (kg) and v = velocity (ms^-1)

•h = planck’s constant

Heisenberg Uncertainty Principle

Says that we can never accurately know the position AND momentum of an electron at the same time, so we cannot talk about the precise location of an electron, just the probability of finding it somewhere

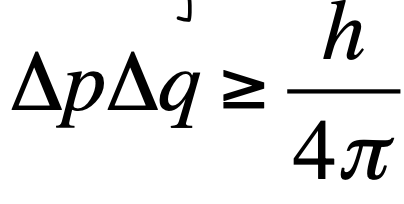
Where 𝚫p = uncertainty in momentum and 𝚫q = uncertainty in position

Wavefunction Ѱ

mathematical description of the wave to describe an electron

Ѱ²

The probability of finding an electron anywhere in a certain space

The Schrödinger Equation (time independent)

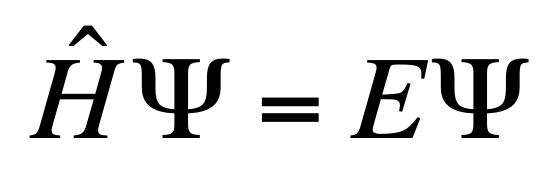
Where H is a Hamiltonian Operator (tells all conditions you need to know — shape, energy, direction of orbital — if you have all the conditions and Ѱ then you can find possible energies

Solution to the Schrödinger equation (only for hydrogen atom)

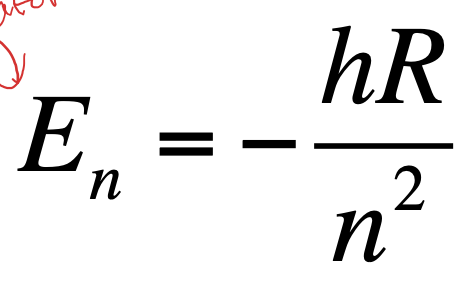
Where n is the principal quantum number and R is the Rydberg constant

It is the same as the Bohr equation but the R includes all the constants

Only possible to solve the equation exactly for two body systems

Four quantum numbers, what they tell us, allowed values

Overall: tell us about the energies and shapes of the electron wavefunctions called orbiatls

n: gives energy of orbital - can be any integer

l: gives shape of orbital - any integer 0 - (n-1)

• l = 0 - s orbital

• l = 1 p orbital

• l = 2 d orbital

• I = 3 f orbital

m_l: orientation of orbital - any whole number from -l to +l

m_s: spin (up/down, left/right ± 1/2)

Orbital

The region of space defined by Ѱ — the possible mathematical wavefunction

Orbital nomenclature

3p_x orbital (n = 3, l = 1,the x signifies orientation which is related to m_l)

radial wavefunction R(r)

contains information about what happens to the wavefunction as the distance from the nucleus increases

Nodes

Where R(r) = 0

Amplitude of Ѱ changes sign

Radial distribution function

Related to R(r)² — the probability of finding an electron in a certain location

The maximum value of the radia, distribution function is the most probable distance from the nucleus for the electron

Nodal planes in p orbitals

where the wavefunction is 0, where there is 0 probability of finding an electron

Nodal planes (and cones) in d orbitals

d_xy, d_yz, d_xz all have nodal planes along axes (y and x; y and z; x and z)

d_x²-y² has nodal planes bisecting x and y axes

d_z² has two nodal cones instead of planes

Energy for a many electron atome

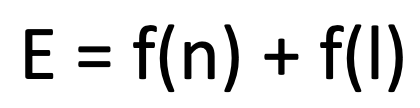
where f(n0 is a function that depends on the principal quantum number, n, and f(l) is a function that depends on the second quantum number, l

Pauli exclusion principle

Says that there cannot be any electrons that have the same set of 4 quantum numbers in the same atom because they will interfere with each other

Aufbau principle

The lowest energy orbitals are filled first (built up from bottom)

Hund’s rule

When filling a set of orbitals with the same energy (degenerate), electrons are added with parallel spins to different orbitals rather than pairing two electrons in one orbital

Pairing and exchange:

• Pairing energy: the energy cost of putting two electrons in the same space (energy increases)

• Exchange energy: a gain in energy when you can exchange identical electrons in degenerate orbitals (more exchanges is better, leads to lower energy: energy stabilization)

  • indistinguishable electrons occur where n, l, and m_s are the same values

• Stability of half and full shells:

  • half full and full are most stable: half full has most possible exchanges and no pairing energy; full has most possible energy minus max number of pairing energies. They maximize the benefit of exchange energy

Aufbau principle in transition metals

4s electrons slightly lower than 3d so they are filled before 3d, but when forming ions the 4s electrons are lost FIRST, before 3d

Limitation of Aufbau principle

If two orbitals are close in energy it can be energetically favorable not to obey aufbau principle but to obey Hunds rule

ex. Cr and Cu

Electron shielding

The energy of an electron mostly depends on how strong its attraction to the nucleus is; if another electron spends time between it and the nucleus then the first electron feels less of an attraction

When an electron wavefunction gets between the nucleus and another electron it can be said to be shielding. This is NOT interference, simply how much of the charge of the nucleus the electron is getting

Effective nuclear charge — definition and equation

How much of the charge of the nucleus an electron actually feels

Z_eff = Z - S

where Z is the total nuclear charge and S is how much the electron is shielded by other electrons

Effective nuclear charge in 1s electrons

1s electrons do not feel the full nuclear charge as the two electrons shield each other — because electrons are wave not particles the shield each other even in the same orbital — also there is some shielding from 2s orbital because it has some electron density close to the nucleus

Intensity/level of shielding in different orbitals (penetration)

If an orbital has an intensity nearer to the nucleus than another orbital, then it is better at shielding

Penetration is the presence of a wavefunction’s intensity close to the nucleus

order of shielding strength by orbital

s>p>d>f

s electrons very good, f electrons horrible at shielding

effects of shielding in chemistry

d-block contraction: d orbitals are bad at shielding so as you go across the transition metals, each successive atom feels a larger Z_eff so the size of the atoms shrink as you go across

types of bonding

Covalent - electron pair shared equally between atoms

Polar covalent- electron pair shared unequally between atoms

Ionic- electrons transferred from one atom to another

Three models of bonding

Lewis model

Valence Bond Theory

Molecular orbital theory

Lewis Model - the octet rule

Atoms in a molecule share electrons to complete a set of 8 electrons. Pairs of electrons not used in bonds are called lone pairs

Dative bond

type of bond where both shared electrons in a bond come from one atom

Limitations of the lewis model

Doesn’t work for some molecules at all (ex NO)

Doesn’t work for transition metal bonding

Doesn’t explain some properties (ex. why is O₂ paramagnetic

Electronegativity

The power of an atom in a molecule to attract electrons to itself

atoms in the top right of the periodic table are the most electronegative

contributes to types of bonding (covalent= no difference in electronegativity; polar covalent= some difference; ionic= big difference)

Valence Bond theory — set of approximations it follows (from Schrödinger equation)

• Orbitals (wavefunctions) can be combined on the same atom to form hybrid orbitals (if needed)

• Orbitals can be combined to form (localized) bonds

• Bonds can be the average of different resonance forms- useful to explain certain situations

Very good for explaining how chemistry happens, especially useful in organic chemistry

Molecular Orbital Theory

Atomic orbitals combine to form molecular orbitals that cna be delocalized over the whole molecule

Assumptions in MO theory

The orbital approximation — Linear combination of atomic orbitals (LCAO)

• if two orbitals come close together they can interfere constructively or destructively

• you cannot destroy or create/invent orbitals

In phase combination

Constructive interference

no nodal plane

bonding orbital

Out of phase combination

destructive interference ( subtraction represents an out of phase combination)

Has a nodal plane

antibonding orbital

Symmetry labels and interference

If orbitals have the same symmetry labels they can interfere, if they don’t, they cannot

Sigma orbitals vs pi orbitals

Sigma: σ Rotation about the nuclear axis does not change the shape of the orbital

Pi: rotation about the nuclear axis changes the shape of the orbital

Parity labels (g vs u orbital)

Even or odd symmetry:

g=gerade (even) — the phase of the orbital does not change upon inversion

u=ungerade(odd) — the phase of the orbital changes upon inversion (draw a line)

Energies of in phase vs out of phase orbitals

In phase (bonding) orbitals tend to have a lower energy

Out of phase (antibonding) orbitals tend to have a higher energy — antibody orbitals given a *

How to calculate bond order

#of filled bonding orbitals - #of filled antibonding orbitals

If bond order is positive when two atoms are combined:

then total energy must have gone down, ion/molecule can be created

non-bonding interactions

when bonding and antibonding interactions cancel out so there is no net interaction (ex. p orbital with sigma symmetry and p orbital with pi symmetry

LUMO

Lowest Unoccupied Molecular Orbital

HOMO

Highest Occupied Molecular orbital

when does paramagnetism occur

unpaired electrons

s-p mixing

when orbitals of the same symmetry can combine/interfere

destabilizes 3σ_g and 3σ_u* orbitals (pushes them much higher in energy)

Pushes 3σ_g orbital above 1pi_u* in energy

stabilizes 2σ_g and 2σ_u* orbitals (pushes them lower in energy)

*trick: goes from 3113 to 1313

s-p mixing stops (isn’t strong enough) after N₂

Heteronuclear diatomics — differences

u and g symmetry labels do not apply

When orbitals have the same energy: MO has equal character of atom 1 and 2

When orbitals have slightly different energy: MO is nearer original energy of atom 2 (lower energy)

When orbitals have very different energy: MO is very near original energy of atoms 2 (lower energy)— has significant character of atom 2