Tree Algorithms - Week 6

What order do trees have and why?

A partial ordering:

→ Levels can be ordered

→ Vertices on the same level are not ordered

The 3 purposes of traversing a tree are:

Serialisation

Search

Tree properties

What do these mean in terms of traversing a tree?

Serialisation → Writing out tree data as a linear sequence

Search → Finding something

Tree Properties → Calculating overall properties of the tree

In terms of a depth first traversal (DFS) what are the definitions of:
Pre-order
Post-order

Pre-order → The vertex is visited before the next step (left side)

Post-order → The vertex is visited after the children are processed (right side)

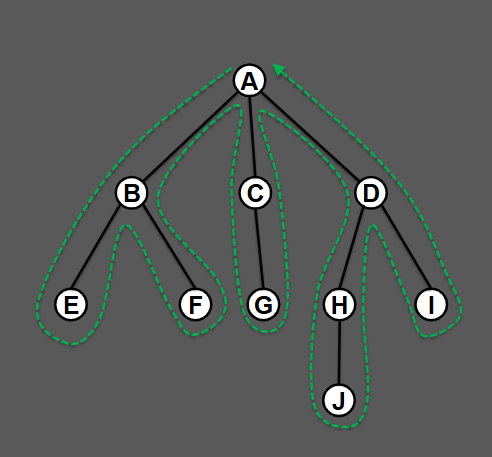
On this tree, what is the pre order?

ABEFCGDHJI

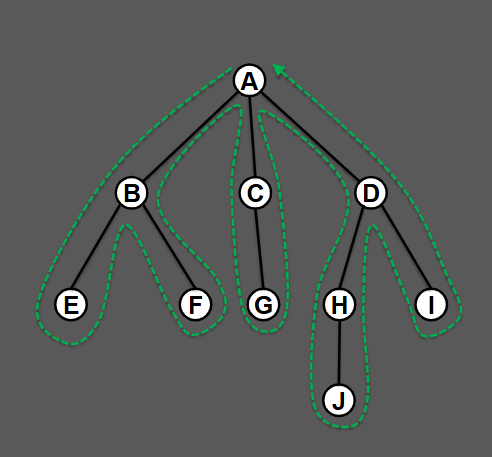
On this tree, what is the post order?

EFBGCJHIDA

What is another variant/order of DFS when a tree is a binary tree, and what does it mean?

In-order, the vertex is visited after the left child and before the right

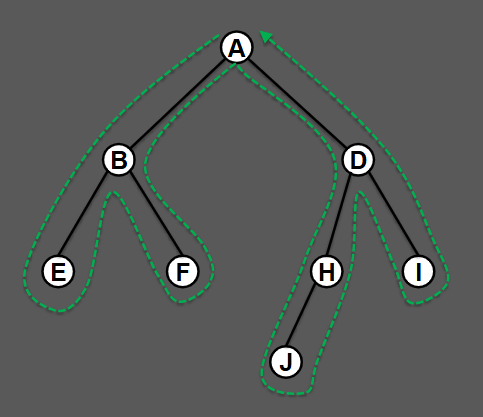
What is the in order of this binary tree?

EBFAJHDI

What is level order traversal?

Breadth first: visit nodes level by level & left to right, at the same time. Visit all siblings before the children

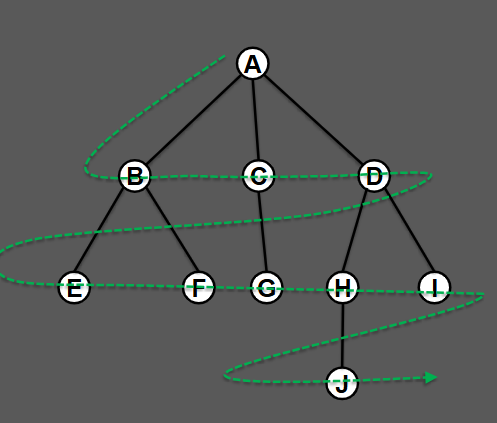
What is the result of a BFS on this binary tree?

ABCDEFGHIJ

A BST is a more organised version of a heap, represented by a binary tree. What can it be used for?

Sets

Dictionaries

Priority Queues

What is the worst case complexity for a BST, and why?

O(n) - because this would mean the height of the binary tree is the number of nodes.

What is the best case complexity for a BST?

Equal children on left and right = height is O(log₂n)

So the best case scenario is O(logn)

What is the algorithm for a search in a BST?

Where are the mins and max for a BST?

Minimum → Always on the far left

Maximum → Always on the far right

What is the algorithm for insert in a BST?

How to delete a childless vertex in a BST?

Delete vertex & the left or right parent link

How to delete a vertex with one child in a BST?

Involves relinking, delete the vertex and reconnect child to left or right link from parent.

(DELETE 9)

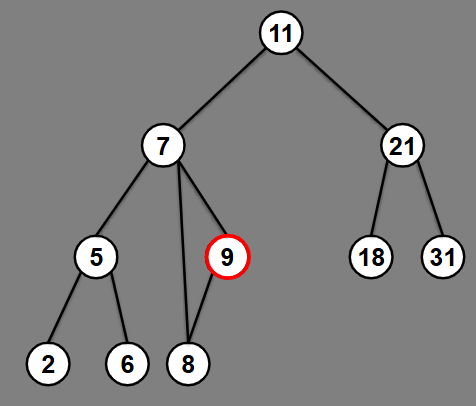
How to delete a vertex with two children in a BST?

Reorganisation of tree.

Find next order from the tree, left most from right subtree.

Replace the vertex to be deleted with the found one.

Delete vertex, at most 1 child.

(DELETE 11)

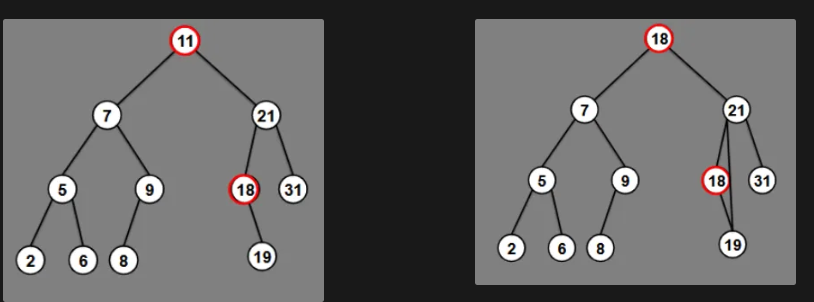
What does balancing trees do?

Means binary trees are not formed poorly so the height is not the number of nodes.

This ensures the complexity is O(logn)

It is done everytime a node is inserted or deleted.

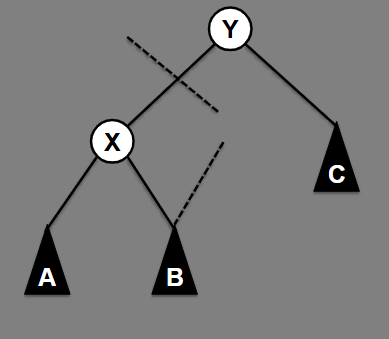
Result of balancing this tree:

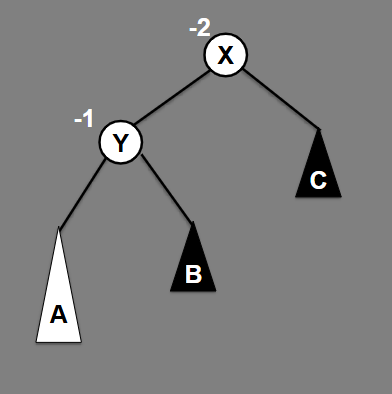
X and Y are vertices, Y is the root. A, B, and C are binary trees (subtrees of the original tree) A≤X ≤Y, X ≤B ≤Y, C ≥Y

Rotate right

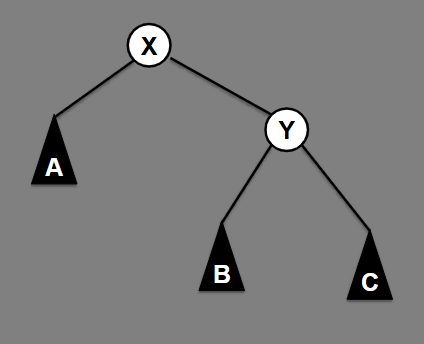
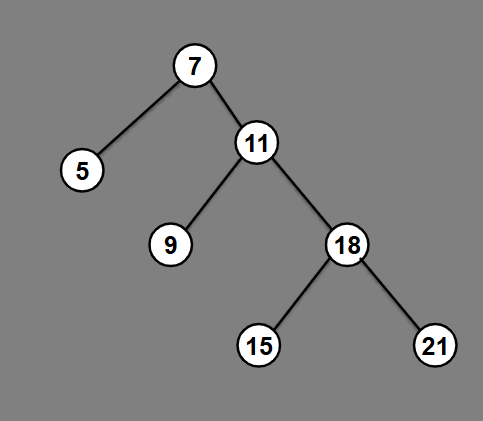
Result of balancing this tree:

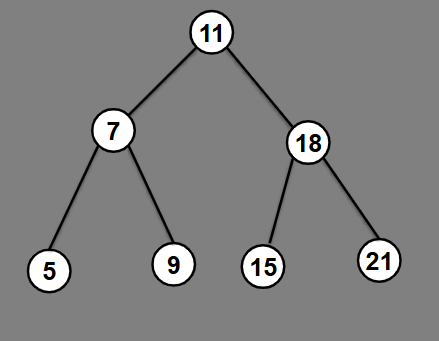
What is an AVL tree?

A self-balancing tree

What does the balancing vertex refer to in a AVL Tree?

To balance, need to measure amount:

BF (balancing factor) = Height(RightSubtree) - Height(LeftSubtree)

Balanced if 𝐵𝐹 ∈ {−1,0,1}

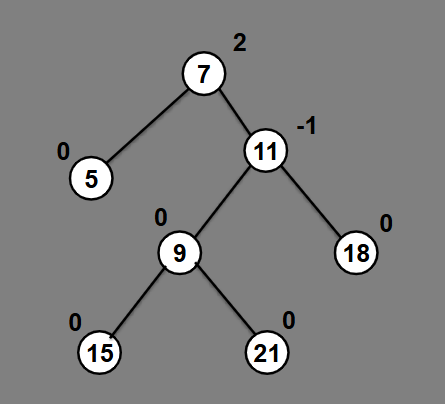
Why is this tree unbalanced?

Because 7 has a BF of 2.

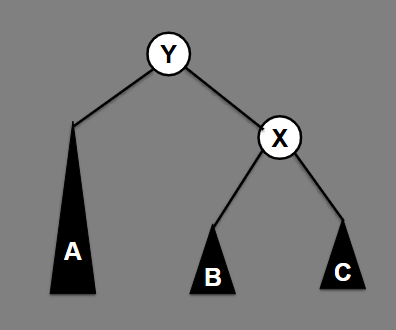
Use a left-left rebalance to balance this tree

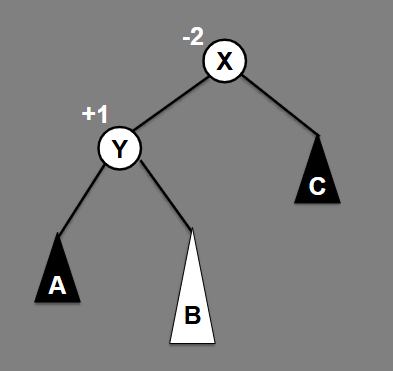
Use a right-left rebalance to balance this tree

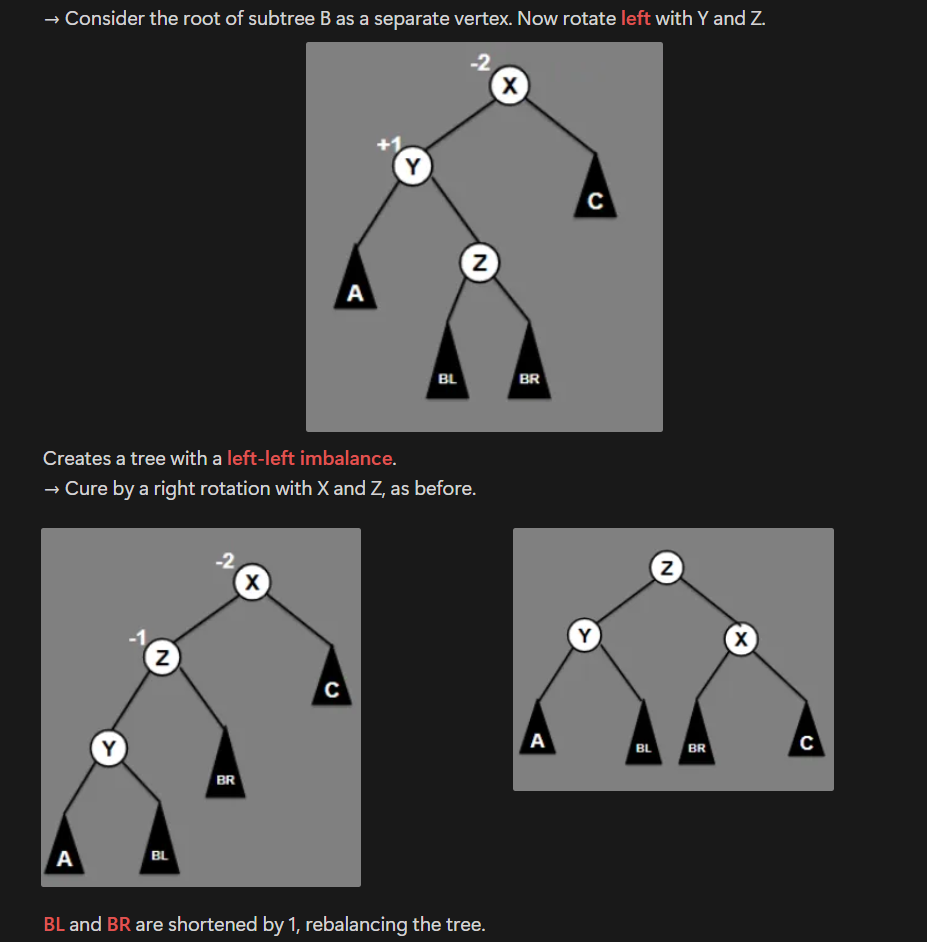
How to do right balances?

The right imbalances: right-right and right-left can be handled the same way with mirror images:

Right-right → Rotate left

Right-left → Rotate right & Rotate left