S170 Definitions and Derivations

Cournot - symmetric firm maximisation problem and EQ

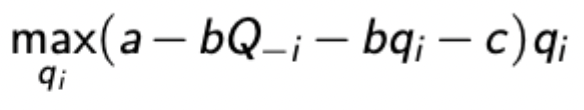
First take FOC wrt q(i), then impose symmetry from BR functions

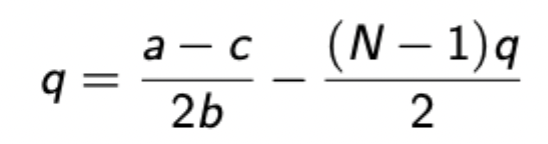
Solve for q then sub in for p and profit

Welfare in Cournot model

Total welfare = consumer surplus + profit

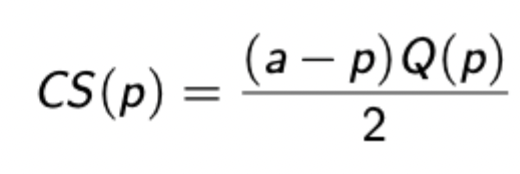
For linear demand* otherwise integrate inverse demand between 0 and q

Cournot: asymmetric case

Same as before but now add up all of the N FOCs to solve for price

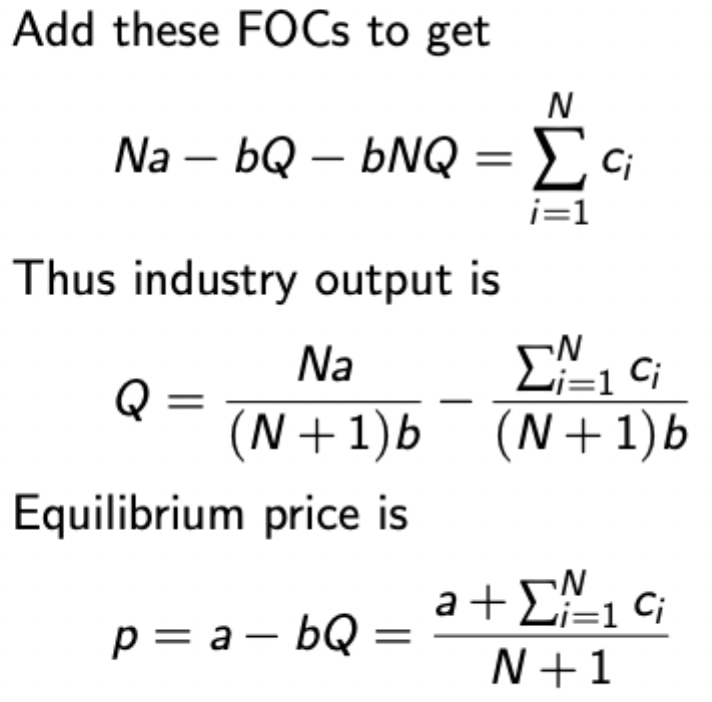
Find EQ production for firm i via its BR function

Cournot with general inverse demand p(Q)

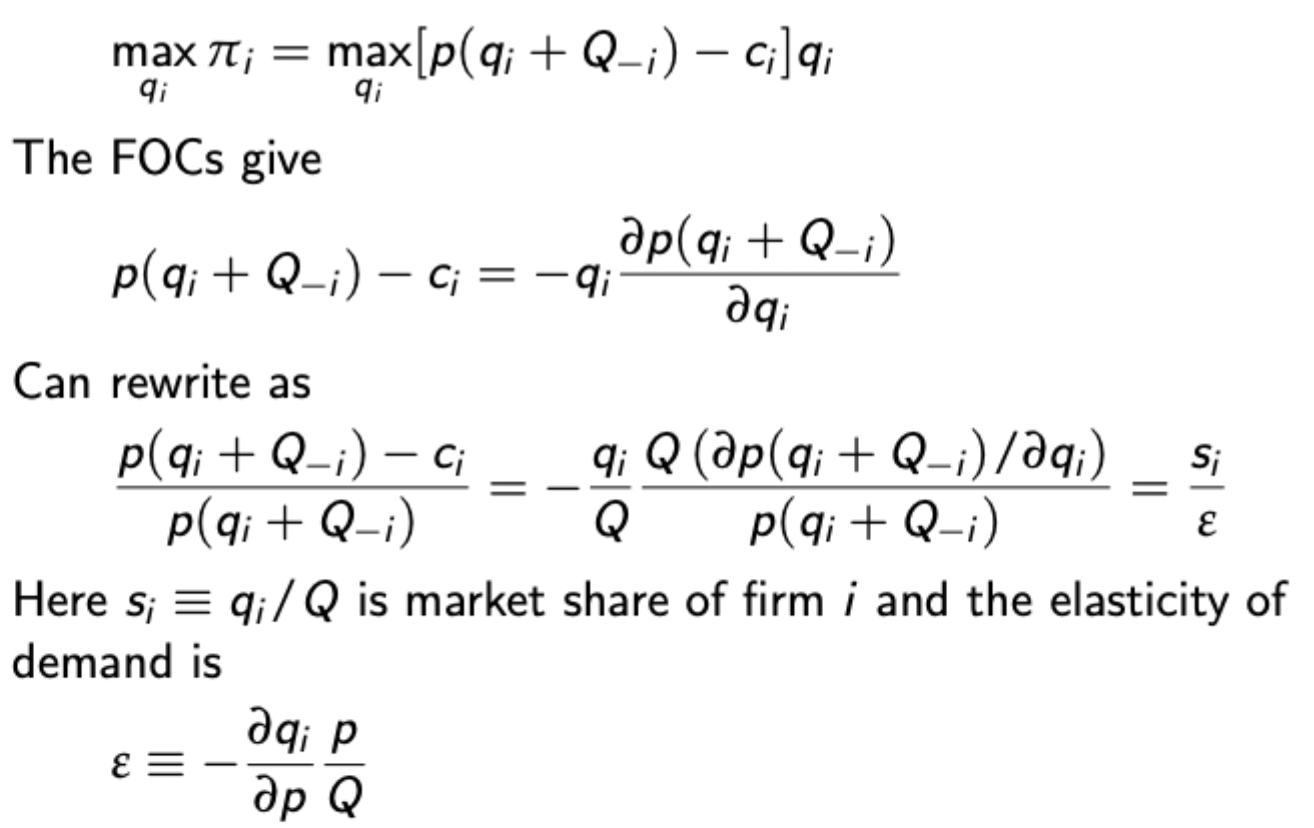
Herfindahl-Hirschman index

Useful measure of market concentration, but ignores costs or efficiencies among firms, which means that it shouldn’t be used on its own to make welfare decisions

Asymmetric case of generalised Cournot

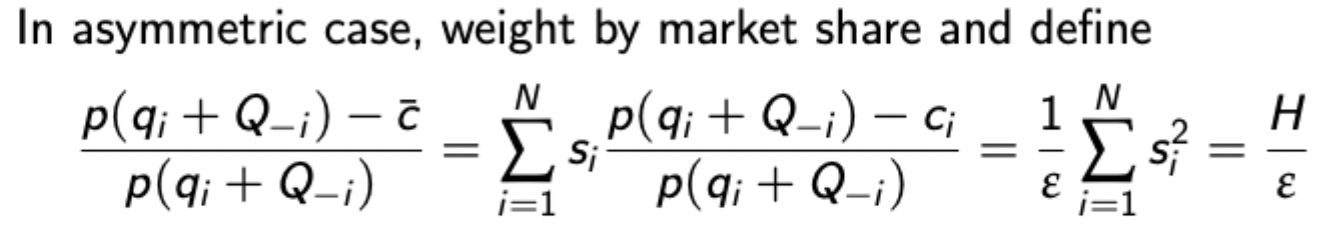
(Where H is the Herfindahl - Hirschman index)

Bertrand EQ

Price = marginal cost for symmetric firms

For asymmetric firms: in any EQ the more efficient firm (lowest MC) sells to all consumers. Any prices for this firm between its MC and the MC of the next most efficient firm can be supported as EQ price set by firm C. The less efficient firm could price below its marginal cost, meaning that the more efficient firm prices at that level (infinitesimally small amount below it), so long as it is above its MC. This reduces profits for the more efficient firm technically without changing the EQ payoff for the less efficient firm(s).

Since pricing below MC for the less efficient firm is a weakly dominated strategy, if firms do not choose a weakly dominated strategy all consumers will buy from the most efficient firm at the marginal cost of the next most efficient firm.

Linear city hotelling model: process (assuming full market coverage)

Locate indifferent consumer by equating utilities from buying from either side of the linear city and solving for x(m) (don’t forget that demand for one is x(m) and for the other is 1-x(m)

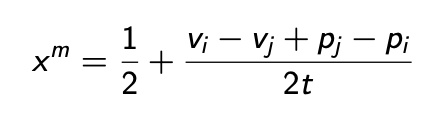
Then derive profit functions from this (p(i) - c)x(m) and (p(j) - c)(1-x(m)) and take FOCs to get best responses, before solving simultaneously. The above example also includes vertical differentiation, (v(i) doesn’t = v(j)) but many examples will have v(i) = v(j) = v.

Welfare in hotelling model with full market coverage

No extensive margin, so no loss to total welfare from a rise in prices - they just redistribute surplus between consumers and firms. Social planner is thus not concerned about prices, and only cares about minimising transport costs as they are ‘lost surplus’. Therefore, with symmetric marginal costs, any symmetric prices will yield a social optimum where x(m) = ½ (in the middle of the city - transport costs minimised).

When firms are asymmetric, transport and production costs must be traded off for welfare.

Welfare in hotelling model without full market coverage

A segment in the middle of the city exists where consumers don’t buy. Firms now have an extensive margin and operate as local monopolists on either side. Extensive margin now means that the social planner cares about prices, and the local monopolists will charge higher than what they would like.

Salop model: key differences from standard hotelling

Now there are N indifferent consumers between each firm equally distributed around the Salop circle. Can solve all problems simultaneously if costs aren’t symmetric or impose symmetry after taking FOCs to solve more easily. Key result here is that the price markup over MC is decreasing in N, indicating greater competition and a greater share of surplus for consumers (works since it implies that greater variety means consumers are more likely to have their specific tastes met).

Random Choice Model: Indirect utility has an unobservable i.i.d component with expected value 0.

Singh-Vives: Set up and FOCs

Note that problems thus become different under Cournot or Bertrand competition

Strategic complements and substitutes: definition

Choice variables are strategic complements if best responses are upward sloping, and strategic substitutes if best responses are downward sloping.

I.e. strategic complements imply that increasing action incentivises others to do the same (i.e. adopting a new technology), strategic substitutes imply the opposite (i.e. public goods)

Singh-Vives key result

In Cournot competition (quantity setting): when products are substitutes they are strategic substitutes, and when they are complements they are strategic complements.

In Bertrand competition (price setting): when products are complements, they are strategic substitutes, and when they are substitutes, they are strategic complements.

Therefore when products are substitutes, Bertrand yields lower prices and higher quantities than Cournot.

When products are differentiated, profits increase in differentiation for both Cournot and Bertrand competition.

Therefore, price competition is fiercer than quantity competition.

Krepps-Scheinkman Model (capacity contraints): Description and justification for EQ

(Firms set capacities then compete on prices in second period)

EQ is to set capacities equal to Cournot quantities. This way, firms aren’t incentivised to raise prices as each firm maximises profits relative to residual demand once the other has sold Cournot EQ q units. Therefore, the best response to the other firm setting K = q© is to set K = q©.

Other ways of setting capacity are inefficient compared to setting it equal to Cournot quantity.

Reasoning: if both firms set capacity such that they can take all market demand, Nash EQ at price stage is p = MC, which when combined with sunk capacity costs will result in negative profits. If firms set capacity below market demand, p = MC cannot be a NE, as the excess demand from firm i can be taken up by firm c to make positive profits, so there is a profitable deviation away from p = MC.

Endogenous product characteristics: hotelling key result with linear transport costs and endogenous locations

Fixed prices: only Nash EQ is for both firms to choose minimum differentiation result

For generic prices: The Price EQ must be in an intermediate region (with no discontinuity) and given by the FOCs. Outside the region the presence of discontinuities mean there is no EQ.

The two firms have the incentive to agglomerate when in the intermediate region, so with strong enough agglomeration, the region shrinks and the price EQ is lost. Therefore, the minimal differentiation result is not robust to endogenous prices.

Hotelling with quadratic transport costs and endogenous locations: key result

Firms want to locate at the extremes of the unit interval. there are two key effects:

Market size: locate close to increase market share

Competition: locate far to reduce the intensity of competition (this effect dominates in the unit interval case)

Shaked-Sutton model (vertical differentiation): indifferent consumer and profit functions

Shaked - Sutton model: key result (full market coverage)

While in the firms’ BR functions, higher differentiation in quality means the price of the lower quality good will fall, it is still possible that higher differentiation means higher price for both in EQ.

Profits also increasing in quality differential, so in EQ there is maximal product differentiation

Shaked - Sutton model: which firm is better off

Monopolist’s problem when choosing product varieties in a Salop city with N locations that can be chosen

Full market coverage so all consumers buy from the firm - the monopolist’s problem is thus the same as the SP - minimise transport costs (then add on that they want to extract all consumer surplus through prices)

Higher N incurs a fixed cost for each variety, so problem is

integral refers to the fact that there are 2N indifferent consumers that will demand 1/2N and then have to pay transport costs t for each ‘unit’ demanded'

Monopolist’s problem with an extensive margin, horizontal differentiation (product variety) model

The location of the marginal customer is given as the point where transport costs equal their valuation - price

Social planner’s problem with an extensive margin in horizontal differentiation (product variety) model

Cournot merger ‘paradox’ and explanation

Insiders and outsiders have identical maximisation problems, so behave the same. The result is a standard Cournot EQ now with N-M+1 firms.

This is because the merger is treated as if all M insiders operate out of only one of their production facilities. MC is constant, no brands, no fixed capital and no synergies.

Derivation of ‘80%’ rule for a merger to be profiable

Holds for p(N) equal to approximately 80% of the market

Why are lots of firms required to merge for a merger to be profitable in a Cournot setting?

Quantities are strategic substitutes, so insiders internalise externalities that their production has on other insiders, thus their reaction function shifts inward after the merger (they produce less), whereas the reaction function of outsiders remains unchanged.

Insiders produce less (although price goes up), but outsiders produce more at a higher price, so merging is a public good and it is better to be an outsider.

Ways to view profitable mergers 1: Fixed costs

Merger reduces fixed costs for all merging entities from MF to F, so it may become profitable even if operating profits fall (i.e. the savings from fixed costs must be large enough to outweigh the losses of operating profit)

Still reduces aggregate output, increases price, hurts consumers and benefits outsiders. Social welfare can go either way depending on magnitude of fixed cost savings.

Ways to view profitable mergers 2: Affecting variable costs (setup)

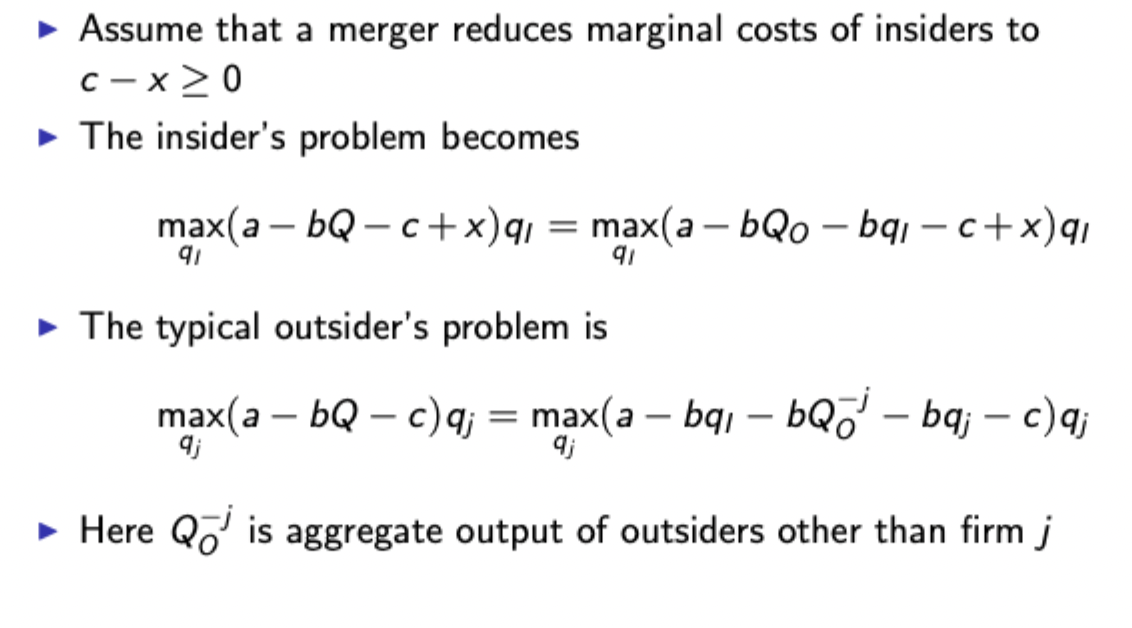
Ways to view profitable mergers 2: Affecting variable costs (finding EQ)

Sub in to find that synergies increase aggregate output and decrease price.

Welfare effects of a merger with synergies

Overall welfare effects need to consider the internal effect (more difficult) and the external effect (effect on outsiders and consumers) which is easier to estimate.

The general conclusion from competition authorities is that synergies need to be much larger for a positive external effect than they do for a positive internal effect, so for a Cournot merger to be socially beneficial, synergies must be very substantial to outweigh negative effects of increased market concentration.

Cournot mergers with firm size (capital): insiders’ and outsiders’ problems

After the merger, the insider has MxK units of capital from all M firms combining, whereas the outsider still only has K

Cournot mergers with firm size (capital): solving for EQ quantities

How to tell if a merger is profitable

Insider profit must be greater than the combined profit of all merging firms pre-merger

Cournot mergers with firm size (capital): merger profitability

Cournot mergers with firm size (heterogenous goods): Key result from adjacent firms merging in a Salop city

The merged firms have monopoly power over the consumers that fall between them, and now only compete with the other adjacent firms for indifferent consumers

All firms increase prices, and the insiders’ market share falls, while the outsiders’ rises. All benefit from the merger, but more so the outsiders (free rider problem)

Consumers are unambiguously worse off since prices rise. There is no extensive margin but now p isn’t symmetric (SP solution has p symmetric to minimise transport costs), so the EQ is not socially optimal.

Alternative: differentiated goods model with an extensive margin: key results

Analysed in the same way as for a standard Cournot merger, giving the following results:

Prices rise, CS falls, insiders’ and outsiders’ profits rise, and the merger decreases overall welfare

Why may a merger be allowed in Canada but not the US or EU

Consumer surplus is the preferred criterion for welfare analysis in the US and EU, so they may disallow mergers tha tincrease social welfare but decrease CS

When is a static cartel stable - Cournot setting

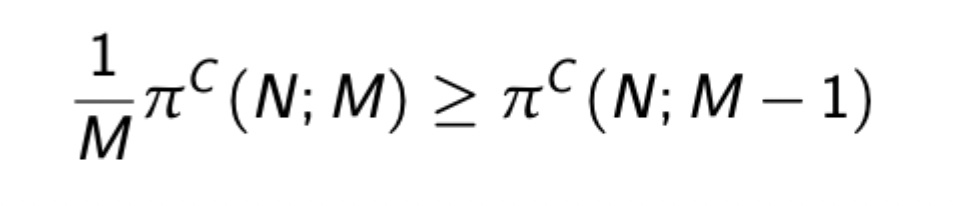
Never satisfied when M>= 3 and M<=N, so no static cartel is stable when N>=3 (only possible when N=2, in which a static cartel replicating monopoly outcome is possible).

Grim trigger strategies

Firms will cooperate as long as no one has deviated in the past, and will play NE strategy after seeing any deviation (the punishment, which is sustainable since it repeats the NE outcome).

Criteria for collusion to be feasible with repeated interactions and grim trigger strategies:

This framework can be applied to many different contexts (homogenous product Bertrand, homogenous Cournot, infrequent meetings and infrequent price changes, and growing markets) - be aware of the niches for each different one.

NOTE THAT FOR COURNOT THE DEVIATION PAYOFF IS NOT THE SAME AS MONOPOLY LIKE IT IS FOR BERTRAND, DEVIATION MEANS PLAYING THE BEST RESPONSE TO THE OTHER FIRM PRODUCING MONOPOLY OUTPUT.

Rotemberg and Saloner: expected discounted values along EQ path and condition for deviation to be unprofitable

Intuitively, the constraint only has to bind in the good state

Rotemberg and Saloner: Partial collusion

Firms agree to set monopoly price in the bad state but cannot collude on a monopoly price in the good state

Possible (thought not implied) to have prices higher in the bad state than in the good state (counter-cyclical prices)

Green and Porter: key dilemma and solution

Price decisions are not observable, only outcomes. Positive demand indicates that the state is good and the firm hasn’t been undercut, but 0 demand could mean the state is bad or that the rival has undercut the firm.

If the firm doesn’t punish the 0 demand, the rival will cheat with impunity, but if 0 demand is always punished then the rival may be punished when innocent.

The solution is 2 have an agreement with 2 phases: a collusive phase with regular collusive outcome, and then a punishment phase that lasts T periods whereby firms convert to NE strategy, triggered by one firm earning 0 profits. This is an example of a stick-and-carrot strategy, as opposed to a grim trigger.

The result is that the switch to 0 profit is because of the change to the bad state - no firm will cheat along the EQ path.

Krepps - Scheinkman model: analysis of when it is optimal for firms to set a price equal to their rival in the second stage, when the rival’s price is 1 - (total capacity)

Showing that it isn’t optimal for firm i to undercut firm j’s price is easy, as the firm would be producing at capacity anyway, so any reduction in the price would not be compensated by additional sales, and revenue (and profit) would fall.

The second part shows that setting a higher price than firm j’s price p* isn’t optimal because p* is already higher than i’s profit maximising price as a residual monopolist for a given capacity level. Hence, in this case, it is not optimal to price either above or below

(q(i) < 1/3 is a feature of a previous question - but the method here is clear)

Krepps - Scheinkman model: analysis of when it is optimal for firms to set a price higher than their rival in the second stage, when their rival sets price equal to marginal cost.

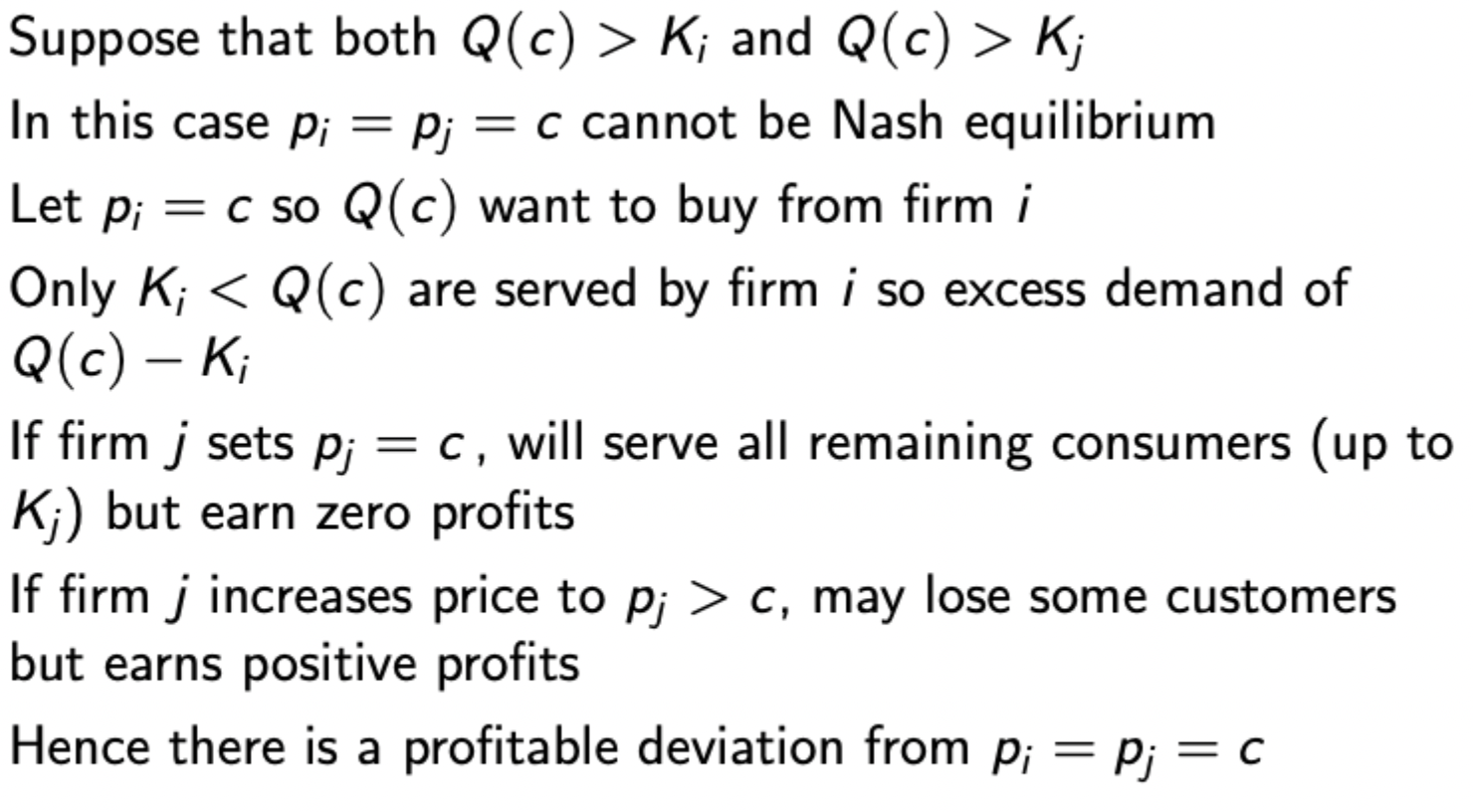
i.e. because for any price above marginal cost, any level of demand will result in higher profits.

Kreps - Scheinkman model: importance of the efficient rationing assumption

• In efficient rationing:

  • All consumers go to the lowest-priced firm first.

  • If that firm can’t serve all demand, the remaining unmet demand is allocated to the next firm(s), preserving the order of consumer willingness to pay.

  • This lets the higher-priced firm sell to consumers who still value the product more than its price — so it can sell out its capacity at its set price, making undercutting unnecessary.

Why It Matters

• Efficient rationing allows residual demand to be allocated in a way that supports higher prices.

• If rationing were random or proportional, the higher-priced firm might sell less than its capacity, discouraging price-setting above marginal cost.

• Thus, efficient rationing removes the incentive to undercut when you're selling out your capacity — it stabilises prices above marginal cost.

Impact on Equilibrium

• With efficient rationing, the price competition stage becomes non-destructive.

• This allows the first-stage capacity decisions to fully determine the competitive outcome.

• So the equilibrium mimics Cournot, even though there's price competition in the second stage.

Differentiated products cartel model: key result

Differentiated products can give partial cartelisation even in static setting.

They can be both internally stable (no leaving - outsider profits with one less firm in the merged entity cannot be bigger than given insider profits) and externally stable (no joining - insider profits with one more firm in the merged entity cannot be bigger than given outsider profits)

Double marginalisation result - successive upstream + downstream monopolies

Each successive firm sets a distortionary markup which doesn’t internalise the fact that it reduces profit to overall vertical structure

Retailer demands too little (akin to perfect complements Cournot duopoly)

Double marginalisation result is generalisable to any downward sloping demand as well as Cournot oligopolies upstream and downstream

How to avoid double marginalisation

1. Two part tariff - set per unit fee equal to marginal cost, so D earns monopoly profit, then set a fixed franchise fee A equal to total monopoly profit to extract all surplus

2. Retail price maintenance (require that the retailer D adds 0 markup)

3. Set a price ceiling or minimum quota (these will not work)

   1. Competition also reduces markup so can reduce double marginalisation effects

Vertical externalities (other than double marginalisation)

1. Moral hazard downstream: U relies on D to provide services, so if D cannot appropriate rents off this, the service will be underprovided

2. Input substitution: If D can substitute between different inputs, differences in market power upstream can distort the input mix downstream

Both can be solved through vertical integration.

Horizontal externalities with upstream and downstream suppliers

If service provision by D increases sales of rival retailers, D may underprovide its services

Vertical integration facilitating collusion

For 2 upstream firms and two downstream firms, if the upstream firms require that the downstream firms both set monopoly price, this is akin to the collusive outcome, then the upstream firm can extract all surplus through a fixed fee. Thus retail price maintenance has facilitated a collusive outcome in the retail market without any actual collusion between retailers.

Vertical foreclosure

Vertically integrated firms can either refuse to buy inputs from other independent firm or refuse to sell to other independent downstream firms. In either case the integrated firm uses its simultaneous presence in both markets to reduce access for rivals.

Aghion Bolton model: entry deterrence through long-term exclusivity contracts, where the marginal cost of the potential entrant is unknown

Key points: entrant will only enter when it is competitive (Bertrand competition), so using the distribution of marginal costs, calculate the probability that the entrant enters the market or doesn’t (i.e. probability that the marginal cost is less than or equal to the incumbent’s). Use these probabilities to calculate expected profits for the incumbent and therefore the expected price without a contract.

When considering a contract, the key things to check is that it is profitable to the upstream incumbent (i.e. leads to higher expected profit) and that it is acceptable to the downstream retailer (cannot reduce retailer’s profits).

Can compare the combined gains from the downstream firm and the upstream incumbent against the losses of the entrant from the contract being signed to determine that the contract decreases social welfare as it creates inefficiently little entry into the market.

Upstream and downstream oligopolies with a vertically integrated firm: strategy of analysis
There are N(u) upstream symmetric firms and N(d) symmetric downstream firms, M are integrated)

1. Argue that in EQ, the independent upstream and downstream firms only deal with each other (i.e. vertical foreclosure from integrated firm - which can be shown just by explaining that it is more profitable for the integrated firm to only buy and sell its own stuff)

2. For a given upstream price, derive the output choices of independent and integrated downstream retailers

3. Aggregate downstream output of independent retailers and note that it must equal independent upstream production

4. Use this to derive induced demand facing independent wholesales

5. Solve for Cournot EQ of game played between independent upstream wholesalers, using induced demand function.

6. This yields EQ quantities (individual and aggregate), price and profits of independent upstream wholesalers

7. Substitute EQ price to obtain EQ quantities of all downstream retailers, prices and profits

Upstream and downstream oligopolies with a vertically integrated firm: effects of increasing the number of firms in the integrated firm (i.e. increasing M)

Additional integration yields lower profits for independents. Since integrated retailers produce more than independent rivals, and earn higher margins, it is more profitable to be integrated retailer rather than independent retailer. Whether additional integration hurts integrated retailers depends on the effect on the downstream price (shown above)

Two effects of vertical integration

Competition effect: integration reduces the number of independent upstream wholesales, which reduces competitive pressure upstream, increases wholesale prices and therefore hurts final consumers through double marginalisation

Efficiency effect: Integration avoids double marginalisation, since it reduces the input costs of integrated retailers, making them more competitive and reducing retail prices

Which effect dominates depends on the number of integrated firms in the industry. Final product price may fall as shown in other card.

Cournot: calculating free entry EQ and effect of higher entry costs

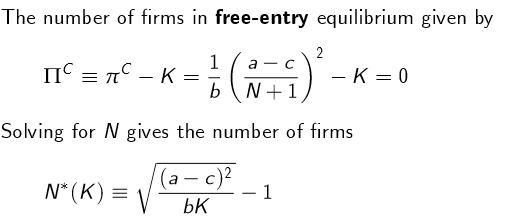
Rising K gives fewer firms, higher output per firm, lower aggregate output, higher price, lower CS and higher operating profits.

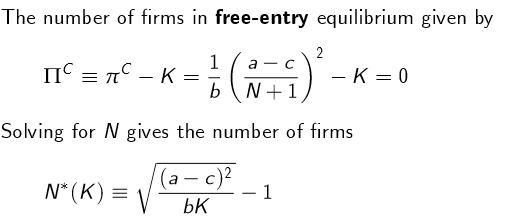
Social welfare and free entry EQ - Cournot

Gross social welfare falls as K rises - fall in consumer surplus higher than rise in operating profits

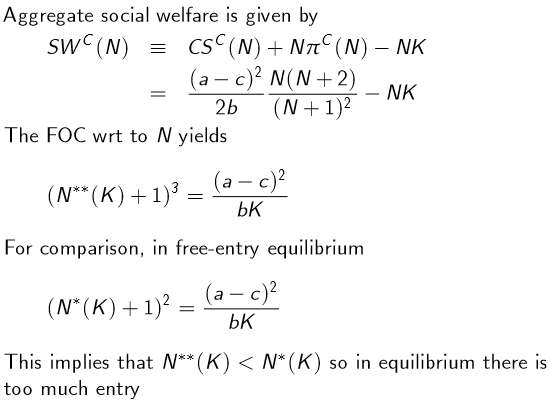
Business stealing effect: lower output per firm despite higher aggregate output. SP doesn’t care where output is coming from but does observe a wasteful duplication of fixed costs K for higher N

Note this is second best - ideally gov’t could control both entry and quantities, but in this case can only control entry.

Salop model: effect of allowing free entry to EQ

Price increases in K, but this has no welfare consequences (just redistributes surplus)

Higher transport costs mean higher margins, which prompts additional entry

Note that firms have market power despite 0 net profit in this case

Could interpret optimal entry as a statement about optimal product variety

Social welfare of entry in the Salop model

Note again the meaning of the integral: there are 2N groups of consumers (each between a firm and an indifferent consumer), that cover a distance of 1/2N on the Salop circle

Too much entry from a social perspective because despite decreased transport costs, which is beneficial to planner, the private incentive to enter is driven entirely by the business stealing effect to achieve operating profits and cover entry cost. Therefore fixed costs are duplicated in a socially sub-optimal way - no reason why EQ should be socially optimal)

Cournot entry strategies for incumbent in a Stackelberg model (incumbent selects quantity then entrant makes a decision)

Blockaded entry: fixed costs are at or above a certain threshold that means that entry isn’t profitable even when the incumbent produces monopoly output. Therefore, i does not need any specific action and will solve monopoly problem. Note that this is not predation - no strategic actions here to reduce entry - predation only occurs when firms are only maximising profit because they have deterred entry.

Entry accommodation: When fixed costs are at or below a threshold that would mean that profits from playing the stackelberg game are higher than what the incumbent would get from deterring entry

Entry deterrence (predation): when fixed costs are between the two thresholds, it is optimal for the firm to set output in such a way that will mean that the entrant would earn lower profits than its break even condition.

Dixit: motivations

Stackelberg model assumes that the incumbent can commit to a certain quantity. if it can’t then post entry competition is standard Cournot.

If i could transform variable costs into fixed costs, this would create a credible commitment to producing more without changing total costs. Can achieve this result through build up of capacity (i.e. Dixit)

Dixit: diagram and explanation

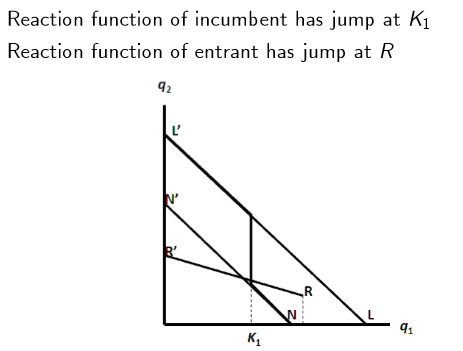
Jump at K1 for incumbent: this indicates the endogenous choice of capacity. If the incumbent sinks cost into capacity, it will produce output more aggressively until it reaches that level, at which point it moves back onto the lower reaction function. Serves as a credible commitment to a more aggressive stance. Remember that committing to that output level involves paying a higher fixed cost.

Jump at R for entrant indicates the fixed costs that must be covered for entry to be profitable. Below a certain output level, not profits become negative and the entrant will not enter.

The outcome depends on the incumbent’s endogenous position for the jump in its BR function, and the entrant’s exogenous jump due to fixed costs.

Dixit: diagrams and outcomes

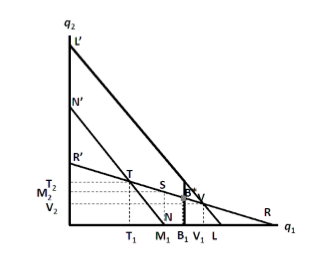
If the entrant’s jump point is between R’ and S, then the incumbent will produce at monopoly output M1 on the inner reaction function (entry is blockaded, maximise profits). (Recall T is standard Cournot EQ point when both firms have same MC)

If the entrant’s jump point is between V and R, then the incumbent gets no additional benefit from capacity commitment to deter entry, and hence gets Stackelberg leader profits from producing at M1.

If the entrant’s jump is at B* (between S and V), the incumbent choosing M1 results in entry occurring, but choosing B1 will deter entry. Therefore, the incumbent can commit to a certain level of output that will deter entry due to the lower variable costs from committing to capacity). If B* is close to S, then deterrence is optimal. If it is close to V, then accommodation is optimal.

Between S and V, the incumbent can choose to commit to a higher output level than M1 (reduces profits, higher costs) by setting capacity to B1 to prevent entry. V indicates the point where entry accommodation is always optimal - no level of commitment can deter entry. As B* gets close to V, accommodation is optimal, whereas when it gets close to S, deterrence is optimal.

Top dog entry strategy

• Goal: Entry deterrence or advantage in post-entry competition.

• Behavior: Over-invest in a way that makes the incumbent tough (e.g., build excess capacity).

• Context:

  • Works in both strategic substitutes and complements under entry deterrence.

  • Works under strategic substitutes with entry accommodation too.

• Example: Building large capacity to credibly commit to high output (as in Cournot).

Lean and hungry look strategy

• Goal: Deter entry by appearing weak or unprofitable.

• Behavior: Under-invest to make it less attractive for the entrant to enter.

• Context:

  • Optimal when investment makes the incumbent soft.

  • Works under both strategic substitutes and complements for deterrence.

  • Also optimal under strategic substitutes with accommodation.

• Example: Avoid investing in fixed costs, reducing attractiveness of market.

Puppy dog strategy

• Goal: Accommodate entry by appearing non-threatening.

• Behavior: Under-invest to soften post-entry competition.

• Context:

  • Occurs under strategic complements, accommodation, and when investment makes incumbent tough.

• Example: Lowering marketing or R&D spending so entrant expects softer competition.

Fat cat strategy

• Goal: Accommodate entry while benefiting from post-entry environment.

• Behavior: Over-invest in a way that makes the incumbent soft (e.g., investing in product quality, which invites entry but also improves margins).

• Context:

  • Occurs under strategic complements, accommodation, and when investment makes incumbent soft.

• Example: Investing in product differentiation or advertising to improve margins, even if it invites entry.

Decomposition of investment effects for entry accommodation

Pure profit maximisation - so you are focusing on the effects of investment by the incumbent on the incumbent’s profits

Decomposition of investment effects of entry deterrence

Strategic effects for strategic substitutes and complements when investment makes the incumbent tough (i.e. makes the incumbent produce more)

Entry deterrence: goal is to make entry unprofitable

• Strategic effect depends on how investment reduces entrant’s profits, so when investment makes the incumbent tough, toughness is beneficial because it discourages entry (top dog strategy)

• Strategic effect is negative for both strategic substitutes and complements

Entry accommodation: maximise profits given that entry occurs

• Strategic substitutes (e.g. Cournot): investment makes the incumbent tough, so the entrant produces less, incumbent produces more, and incumbent profits rise (top dog strategy)

  • Strategic effect is positive

• Strategic complements (e.g. Bertrand): the entrant will also become more aggressive, so prices will fall, and incumbent profits fall (hence puppy dog strategy - incumbent is ‘nice’ to entrant and underinvests to prevent too high competition)

  • Strategic effect is negative

Strategic effects for strategic substitutes and complements when investment makes the incumbent soft (i.e. makes the incumbent produce less)

Entry deterrence: goal is to make entry unprofitable

• Strategic effect depends on how investment reduces entrant’s profits, so when investment makes the incumbent soft, it encourages the entrant. Investment raises entrant’s profit, which hurts the objective of deterring entry (hence under-invest with lean and hungry look strategy)

• Strategic effect is positive for both strategic complements and substitutes.

Entry accommodation: maximise profits given that entry occurs

• Strategic substitutes (e.g. Cournot): investment makes the incumbent soft, so the entrant will expand aggressively and the incumbent loses market share and profit if it invests more (hence lean and hungry look strategy)

  • Strategic effect is negative

• Strategic complements (e.g. Bertrand): investment makes the incumbent compete less, so the entrant does less. Market is softer overall with higher prices, so incumbent profits rise. Incumbent thus over-invests (fat cat strategy) to maintain this environment

  • Strategic effect is positive

Persuasive advertising

Informative advertising

Dorfman Steiner rule and derivation (monopolist facing a demand function that depends on both the price and the level of advertisement)

Monopolist should set price and advertisement such that the ratio of advertisement expenditure and sales revenue equals the ratio of advertisement elasticity of demand and price elasticity of demand.

Note that advertising doesn’t create market power, rather market power facilitates advertising to be effective. No role for advertising in perfect competition.

Informative advertising model: hotelling with consumers that may receive ads from 0, one of the firms, or both:

Persuasive advertising model: hotelling with vertical differentiation, and advertising that affects relative valuations.

Profits decrease because of advertisement. Ads are costly but don’t alter EQ prices, and thus both would be better off without the ability to advertise. This is essentially a prisoner’s dilemma game.

If ads were to shift the distribution in own good’s favour they would then be a type of wasteful competition

if ads increased perceived product differences, then ads relax price competition and would be a public good.

Therefore, conclusions about persuasive advertising depend delicately on the model choice.

Guidance for hotelling model without full market coverage

Each firm acts as a local monopolist. Key point is that now the ‘indifferent consumer’ is not indifferent between buying from either of the two firms, he is indifferent between being in the market and not. Hence instead of equating demands for the two indifferent consumers, you equate demand to 0.

When deriving a condition for full market coverage, you are essentially ensuring that for every consumer, buying from at least one of the firms ensures weakly positive utility. This is shown as below:

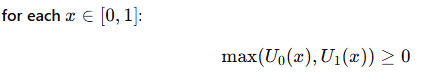
Where:

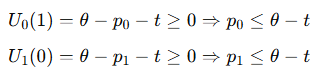
Expressions only differ in prices, hence

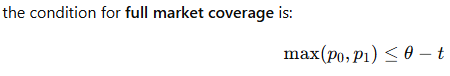
This ensures that even the worst off consumer (i.e. the one farthest from both firms) is willing to buy.

Solving for blockaded entry (Cournot)

Work out entrant’s best response function if entry occurs, then sub in monopoly output from the incumbent. Sub this into the break even condition to derive a condition for entry costs for blockaded entry.