AP calculus AB general info

important information from each unit

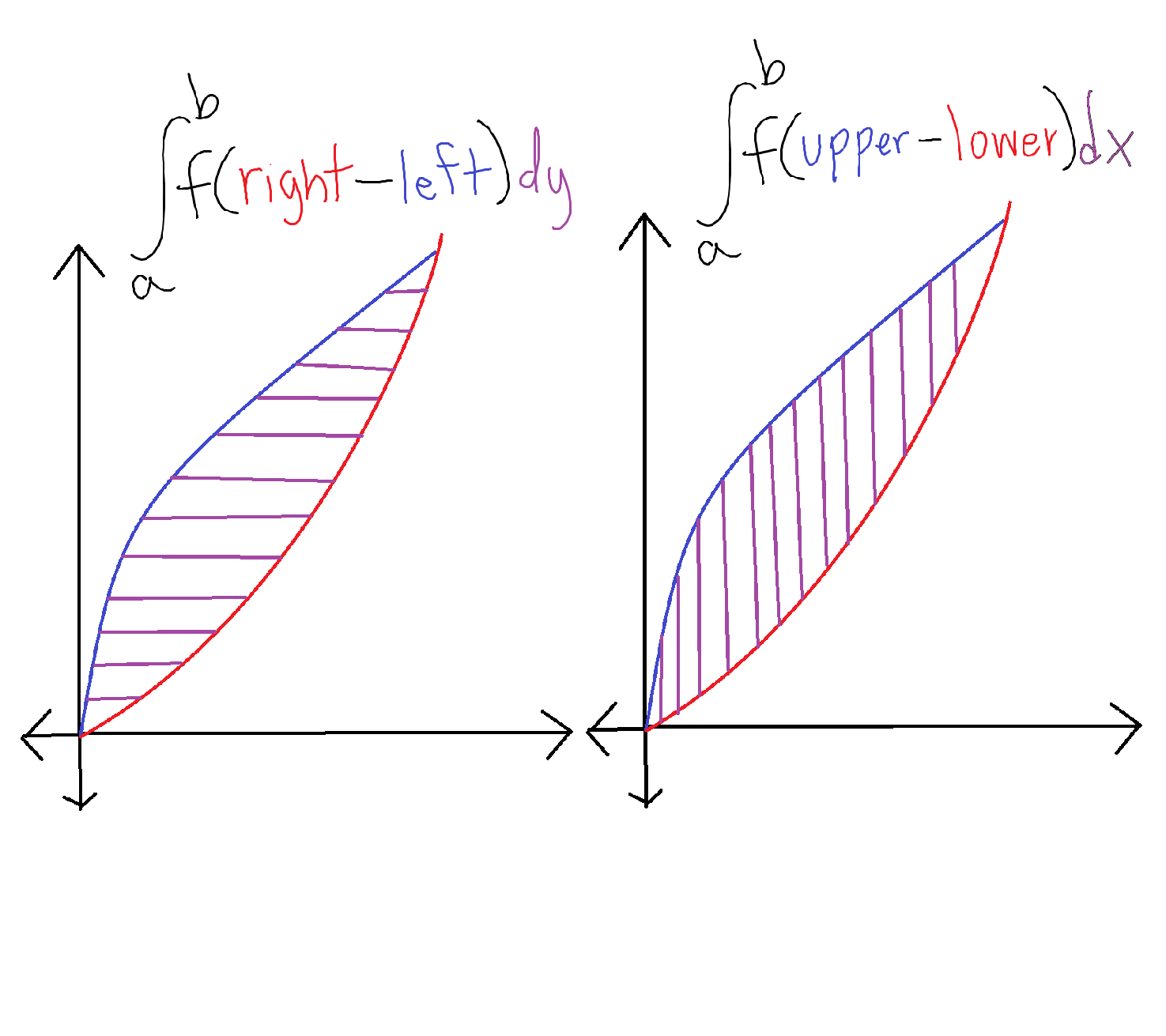
area between curves

_a∫^b(top-bottom)dx

or:

_a∫^b(right-left)dy

volume of a revolution

π_a∫^b[R(x)]²dx

where R(x) is the radius of the function (usually the area between two curves)

volume of a revolution (washers)

π_a∫^b[r(outer)²-r(inner)²]dx

where r is the radius function

volume by cross section

_a∫^b[A(x)]dx

where A(x) is the are for the shape of the cross section

∫(1/x)dx

ln|x| + C

∫e^xdx

e^x + C

∫csc(x)cot(x)dx

-csc(x) + C

∫sec(x)tan(x)dx

sec(x) + C

∫csc²(x)dx

-cot(x) + C

∫sec²(x)dx

tan(x) + C

∫sin(x)dx

-cos(x) + C

∫cos(x)dx

sin(x) + C

∫xⁿdx

(xⁿ⁺¹)/(n+1) + C

Fundemental Theorum of Calculus (Part 1)

_a∫^bf(x)dx = F(b) - F(a)

where F’(x) = f(x)

Fundemental Theorum of Calculus (Part 2)

d/dx_a∫^xf(t)dt = f(x)

and

d/dx_a∫^uf(t )dt = f(u) * u’

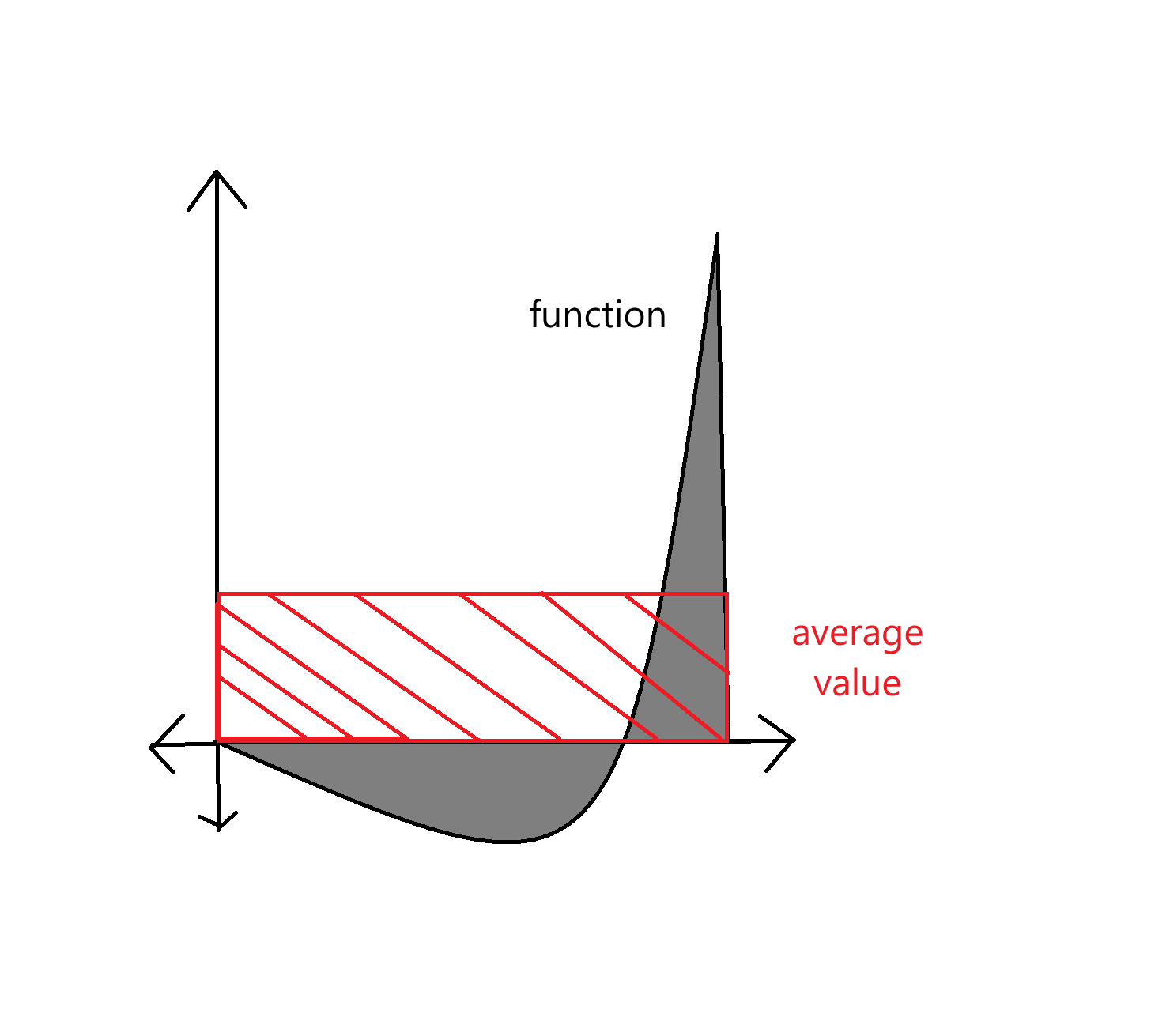
average value of a function

(1/(b-a))_a∫^bf(x)dx

trapezoidal Reiman sum

_a∫^bf(x)dx over n sumbintervals = [(b-a)/2n](f(x_n) + f(x_n-1)…)

right Reiman sum

_a∫^bf(x)dx over n sumbintervals = [(b-a)/n][f(x₁) + f(x₂)… + f(x_n)]

left Reiman sum

_a∫^bf(x)dx over n sumbintervals = [(b-a)/n][f(x₀) + f(x₁)… + f(x_n-1)]

midpoint Reiman Sum

_a∫^bf(x)dx over n sumbintervals = [(b-a)/n][f((a+c)/2) + f((d+b)/2)…]

_a∫^bf(ax)dx

[F(ax)]/a + C

_a∫^af(x)dx

0

_a∫^bc*f(x)dx

c*_a∫^bf(x)dx

_a∫^bf(x)±g(x)dx

_a∫^bf(x)dx ± _a∫^bg(x)dx

_a∫^bf(x)dx + _a∫^cf(x)dx

_a∫^cf(x)dx

_a∫^bf(x)dx

-_b∫^af(x)dx

_a∫^b c dx

c(b-a)

a critical point on f(x)

where f’(x) = 0

or

f’(x) = DNE

a point of inflection on f(x)

where f’’(x) = 0 or DNE

and

where f’(x) has a critical point

if f’’(x) > 0

f’(x) is increasing

and

f(x) is concave up

if f’’(x) < 0

f’(x) is decreasing

and

f(x) is concave down

if f’(x) is decreasing

f(x) is concave down

if f’(x) is increasing

f(x) is concave up

if f’(x) > 0

f(x) is increasing

if f’(x) < 0

f(x) is decreasing

particle motion equations

position/displacement: x(t) or ∫v(t)dt

velocity: v(t) or x’(t) or ∫a(t)dt

acceleration: a(t) or v’(t) or x’’(t)

distance: ∫|v(t)|dt

a particle is slowing down

if v(t) and a(t) have opposite signs

a particle is speeding up

if v(t) and a(t) have same signs

a particle is moving toward the origin

if x(t) and v(t) have opposite signs

a particle is moving away from the origin

if x(t) and v(t) have the same sign

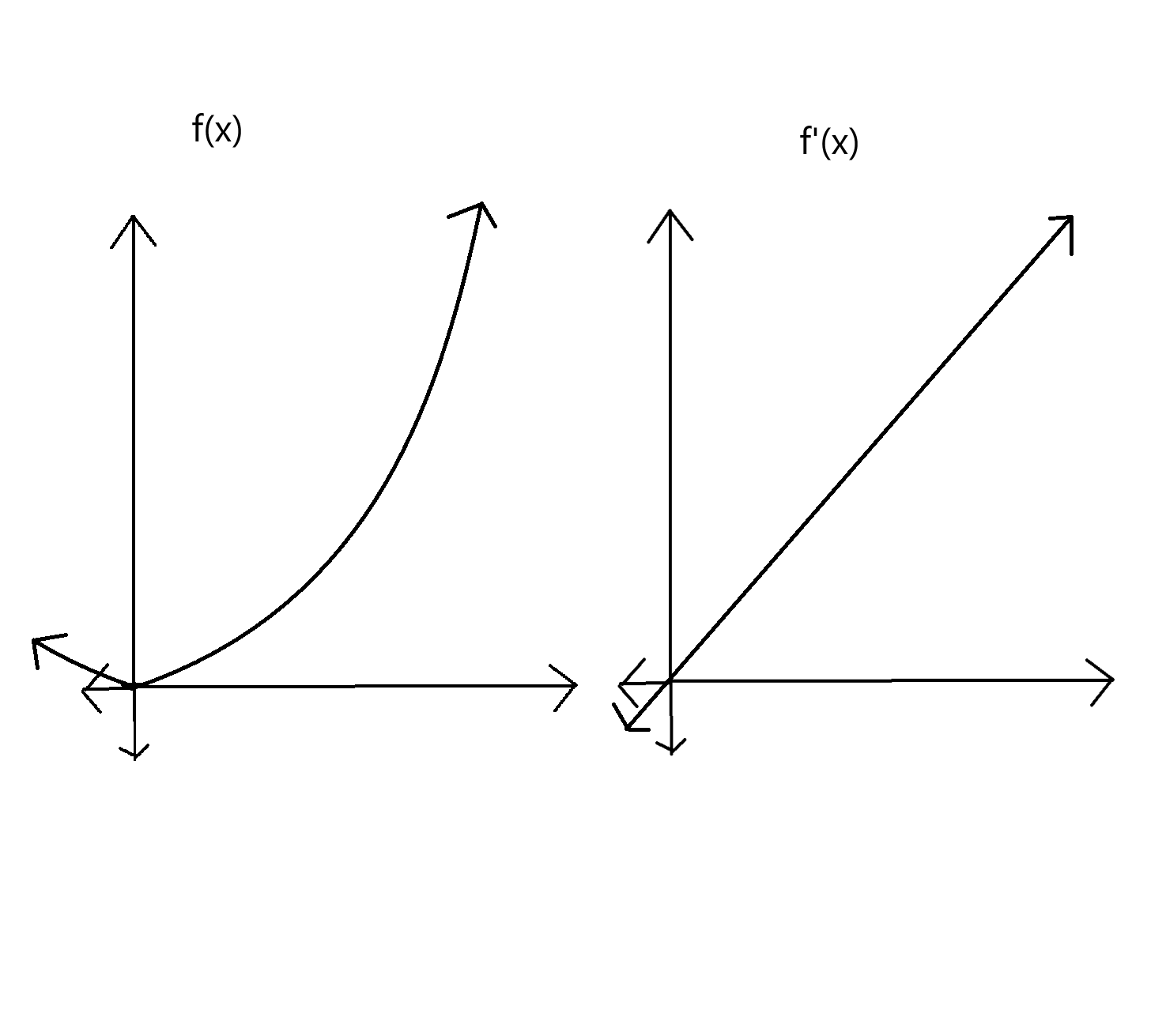
a local minima is where…

f’(x) crosses the x axis from negative to positive

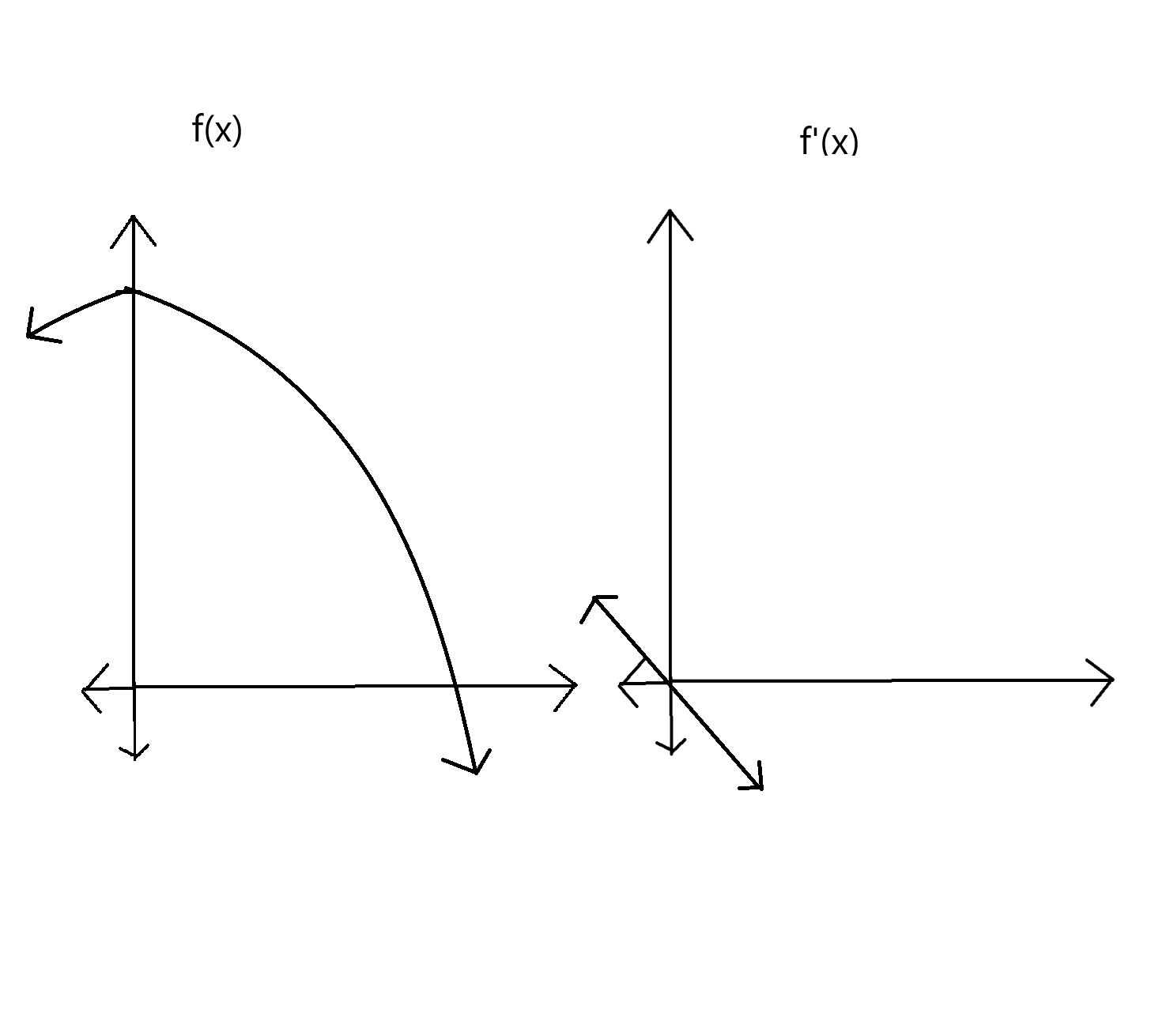
a local maxima is where…

f’(x) crosses the x axis from positive to negative

a function is changing direction when…

f’(x) changes sign

Intermediate value theorem (IVT)

If f(x) is continuous on a closed interval [a,b], then for every k ∈ (f(a), f(b)), there exists a c ∈ (a,b) such that f(c) = k.

AKA: f(x) goes through every x value between a and b and through every y value between f(a) and f(b)

Mean value theorem (MVT)

If f(x) is continuous on a closed interval [a,b] and differenciable on an open interval (a,b), then there exists a c ∈ (a,b) such that f’(c) = [f(b)-f(a)]/(b-a)

AKA: there is an f’(x) on the interval (a,b) which is equal to the average rate of change between a and b

Extreme Value Theorem (EVT)

If f(x) is continuous on a closed interval [a,b], then f(x) takes on a maximum and minimum value on [a,b] and they must occur at an endpoint or critical point

*if (a,b) is an open interval, this could be true but not necessarily

differentiability on a graph

f(x) is not differentiable if f(x) is discontinuous or if it is at a corner, cusp, or vertical tangent

differentiability

a function is differentiable when:

1) f(x) is continuous at point c

2) lim f(x) = lim f(x)

^{x→ c+ x→c-}

³⁾ f(c) ≠ ∅

implicit differenciation

for f(x) = u + y where y is part of a function

f’(x) = u’ * y’

y’ = u’/f’(x)

constant multiple rule

d/dx c*f(x) = c*f’(x)

quotient rule

for f(x) = u/v,

f’(x) = (v*u’ - u*v’)/v²

sum + difference rule

d/dx(f(x) ± g(x)) = f’(x) ± g’(x)

product rule

for f(x) = u*v

f’(x) = v*u’ + u*v’

chain rule

d/dx f(g(x)) = f’(g(x)) * g’(x)

power rule

for f(x) = xⁿ, f’(x) = nx^n-1

g’(x) where g(x) = f^-1(x)

1/f’(g(x))

d/dx log_bu

u’/(u*lnb)

d/dx e^u

e^u * u’

d/dx e^x

e^x

d/dx a^x

a^x * lna

d/dx a^u

a^u * lna * u’

d/dx lnu

u’/u

d/dx log_bx

1/xlnb

d/dx lnx

1/x

d/dx sinx

cosx

d/dx cosx

-sinx

d/dx cotx

-csc²x

d/dx secx

sec(x)tan(x)

d/dx cscx

-csc(x)cot(x)

d/dx tanx

sec²x

d/dx arccsc(x)

-1/(|x|√(x²-1))

d/dx arcsec(x)

1/(|x|√(x²-1))

d/dx arctan(x)

1/(1+x²)

d/dx arccot(x)

-1/(1+x²)

d/dx arccos(x)

-1/√(1-x²)

d/dx arcsin(x)

1/√(1-x²)

d/dx C

0

lim sin(ax)/bx

^x→0

a/b

lim sin(x)/x

^{x →0}

1

lim (1-cosx)/x

x →0

0

first limit definition of a derivative

lim (f(x+h) - f(x))/h

^{h → 0}

second limit definition of a derivative

lim (f(x)-f(c))/(x-c)

^{x → c}

l’hôpital’s rule

if lim f(x)/g(x) = 0/0 or ∞/∞ and f(x) and g(x) are differenciable on the interval (a,b) contianing c and g’(x) ≠ 0 for all x in (a,b) except c, then

lim f(x)/g(x) = f’(x)/g’(x)

^{x → c}

to find lim f(x)

^x→c

1) plug in c

• if you get an indeterminate: factor, multiply by a conjugate, or use l’hôpital’s rule

• if you get a value over 0 (#/0), you have an asymptote. Plug in a number very close to c to figure out what kind.

• if you get a normal value, that’s the limit!

to find lim f(x)

^x→∞

look at end behavior

• for polynomials:

  • even degree + positive = ∞ (and vise versa)

  • odd degree + positive = ∞ as x goes to the right (and vise versa)

• for exponential functions:

  • e^x and a^x trend towards infinity on the right and 0 on the left

  • e^-x and a^-x are the opposite

• for rational functions:

  • if numerator>denominator, ∞

  • if denominator> numerator, 0

• for other functions (ex: lnx/e^x):

  • treat it like a rational function. If the numerator grows faster, it’s ∞, if the denominator grows faster, it’s 0.

continuity

a function is continuous if:

1) lim f(x) exists

^x→c

2) f(c) exists

3) lim f(x) = f(c)

^{x → c}

types of discontinuity

1) jump

2) removable

3) infinite discontinuity/asymptote