StemUp: OCR A A level Physics 5.3: Oscillations

How do oscillations come about? (4)

- An object is displaced from its equilibrium position.

- The object experiences a force thus has an acceleration towards equilibrium.

- The object doesn't come to rest immediately so continues past equilibrium until it has reached maximum displacement on other side.

- The process repeats and the object oscillates about the equilibrium position.

What is the defintion of displacement? (1)

Displacement is the distance from equilibrium position.

What is the definition of amplitude? (1)

Amplitude is the maximum displacement from equilibrium position.

What is the defintion of period? (1)

Period is the time taken to complete one full oscillation.

What is the defintion of frequency? (1)

Frequency is the number of complete oscillations per unit time.

What is the definition of angular frequency? (1)

Angular frequency is defined as the product of frequency and 2π.

What are the equations for angular frequency? (2)

- ω=2πf in terms of frequency.

- ω=2π/T in terms of period.

What is the definition of phase difference? (1)

Phase difference is the difference in displacement between two oscillating objects of the displacement of an oscillating object at different times, symbol φ.

What are the units of phase difference? (1)

Phase difference is dimensionless as it is measured in radians.

What is meant by an isochronous oscillator? (1)

An isochronous oscillator is an oscillator in which the period is independent of amplitude.

Why is a simple pendulum an isochronous oscillator? (1)

Because larger amplitude increases average speed, the pendulum still takes the same time for one oscillation.

What is the definition and defining equation of simple harmonic motion? (2)

- Simple harmonic motion is motion is oscillations in which the acceleration of the object is directly proportional to its displacement and always acts towards equilibrium.

- The defining equation is a=-ω²x.

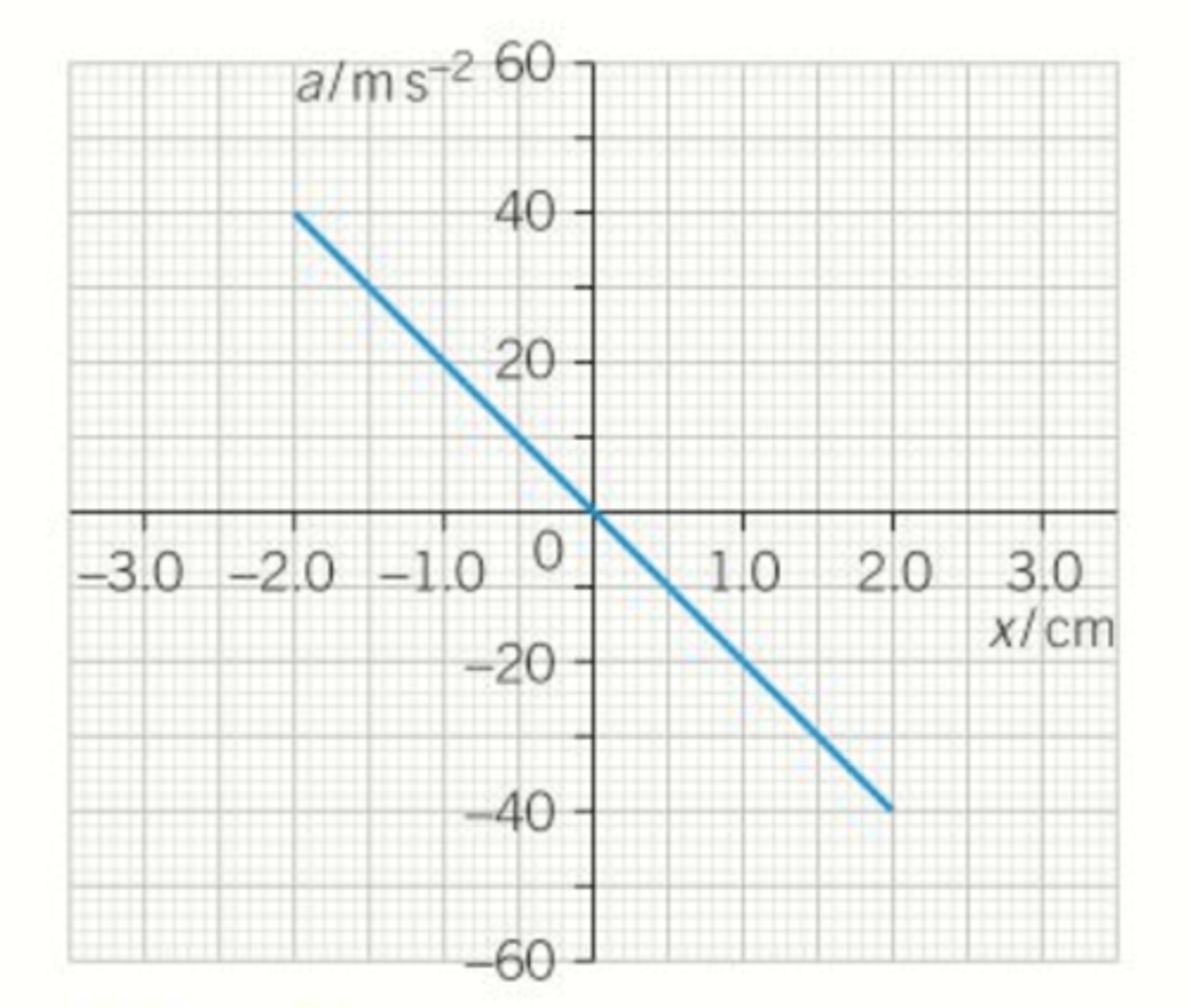
Draw and explain a graph of acceleration versus displacement for a simple harmonic oscillator. (2)

- The graph is a straight line through the origin with negative gradient because a=-ω²x.

How would you accurately determine the period and frequency of simple harmonic oscillations in the lab? (5)

1. Use either a mass-spring system or pendulum to generate the oscillations

2. Place a fiducial marker at the equilibrium position to provide a clear reference point for timing.

3. Displace the oscillator slightly ensuring a small amplitude and release it, then use a stopwatch to time a large number of complete oscillations eg. 10T.

4. Divide the total time by the number of oscillations to obtain the average period T in order to reducing the reaction time error.

5. Calculate the frequency using f=1/T.

Why, when experimentally determining the time period of simple harmonic oscillations, is it sensible to record the time taken for several oscillations, rather than a single swing? (2)

- Reaction time error is a large fraction of the total time if only one oscillation is measured.

- Timing many oscillations and then dividing by the number reduces the percentage uncertainty in the period.

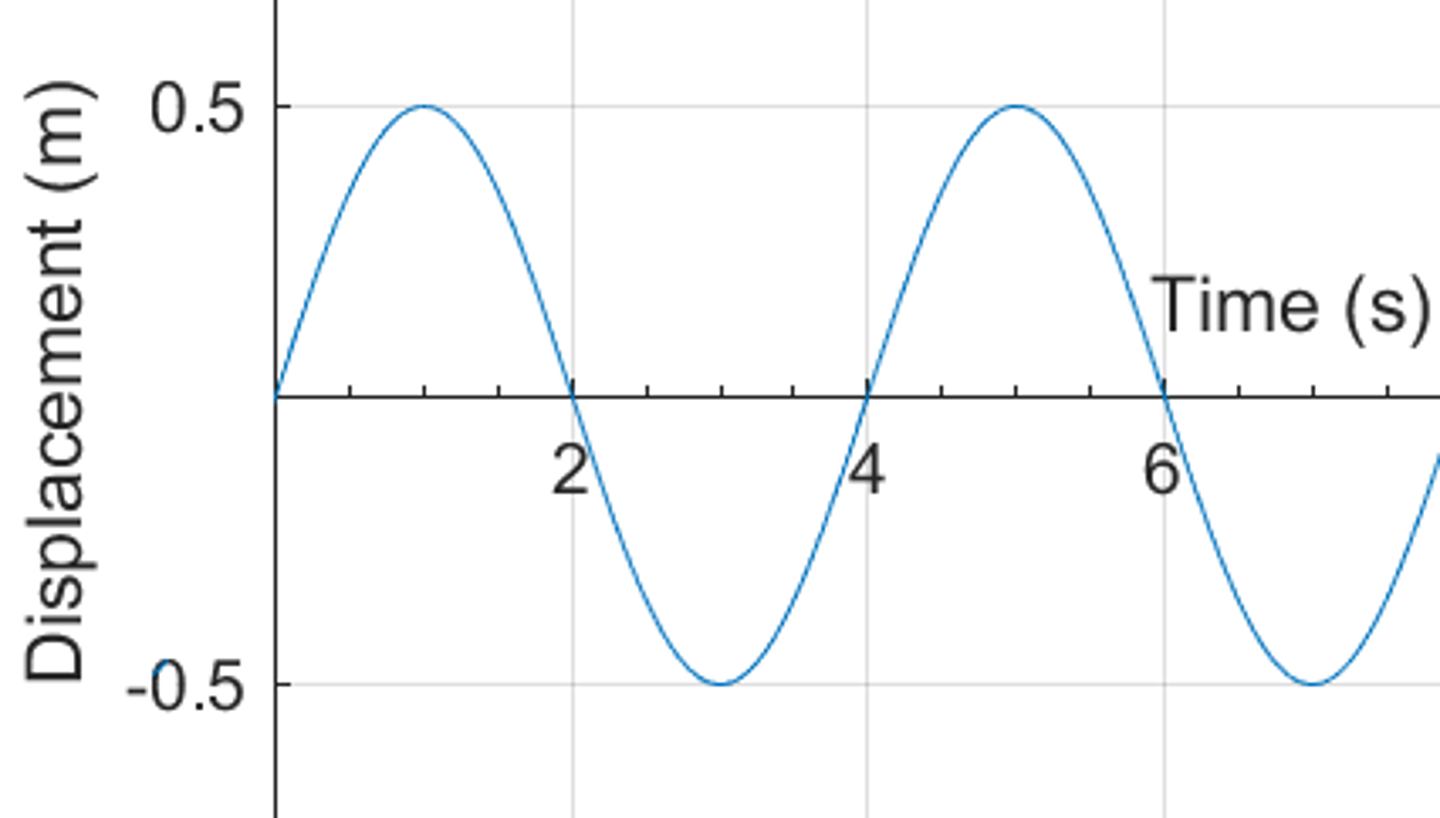
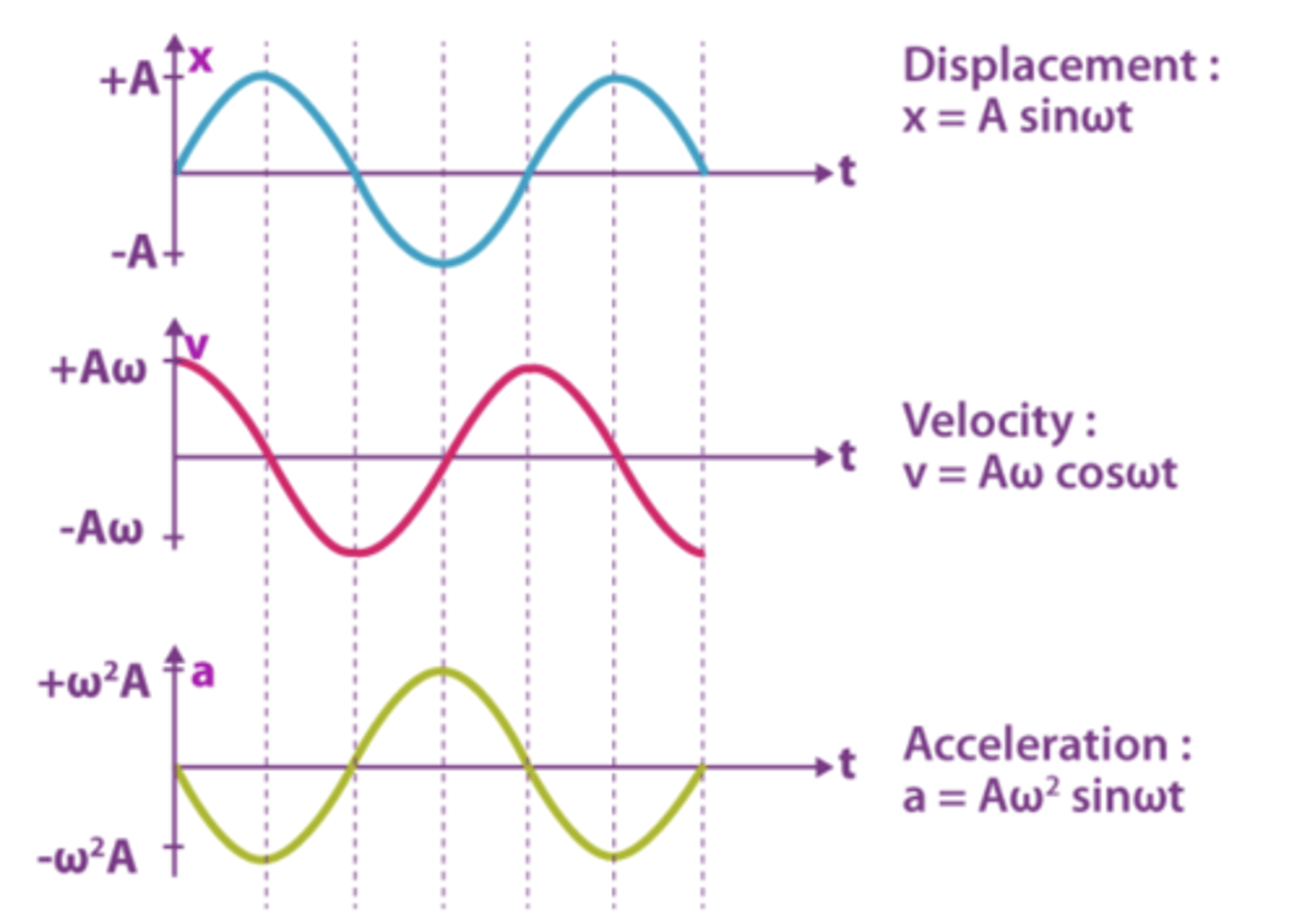
Draw and describe the graph of displacement against time for a simple harmonic oscillator. (2)

- The graph is sinusoidal and constant in period and amplitude.

What are the solutions to the SHM equation? (2)

- x=Acos(ωt).

- x=Asin(ωt).

Which solution to the SHM equation would you choose in different cases? (1)

The equation used depends on the graph of displacement against time: if at t=0 the object is at equilibrium, use the sine one one, but if the object starts at amplitude at t=0, use the cosine one.

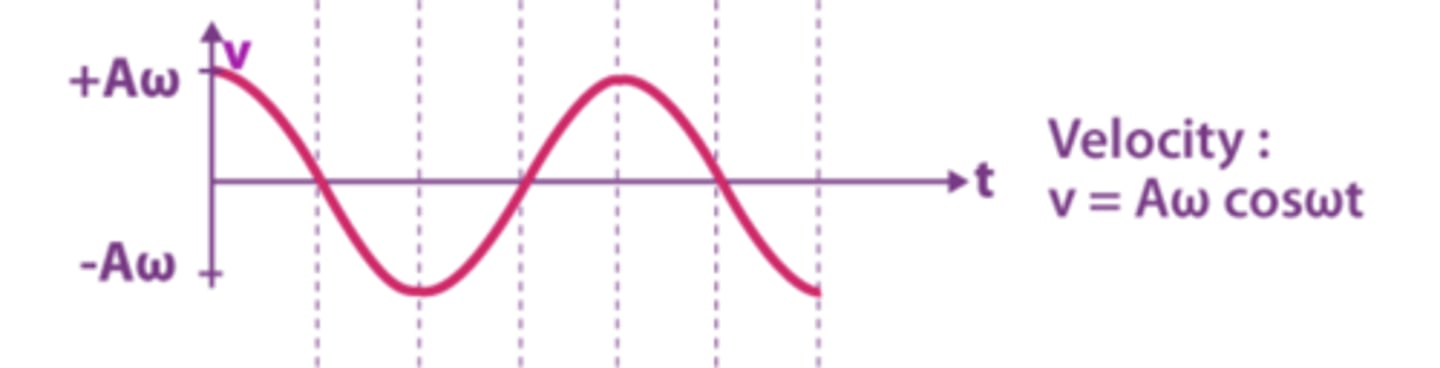
Draw and describe the graph of velocity against time for a simple harmonic oscillator. (2)

- The graph should be sinusoidal and represent the time derivative of displacement as v=dx/dt.

What is the equation for the instantaneous tangential velocity at any point during simple harmonic motion? (1)

Velocity is given by v=±ω√(A²-x²).

At which point during SHM is velocity maximum? (2)

- The velocity is maximum when displacement is zero, ie. when the oscillator is moving through equilibrium.

- This is because when x=0, v=±ωA and in all other cases when x≠0, the velocity has a smaller value as the part in the square root is A²-x².

What is the equation for maximum tangential velocity in simple harmonic motion? (1)

vmax=ωA.

Derive the equation for maximum tangential velocity in simple harmonic motion. (1)

The velocity is maximum when the oscillator is moving through equilibrium ie. when x=0, so substitute in x=0 into v=±ω√(A²-x²).

What would be the effect on velocity if angular frequency increases? (2)

- The oscillator covers the same distance in less time so vmax must increase.

- Also by v=±ω√(A²-x²), v∝ω.

How does acceleration vary in SHM over the course of an oscillation? (3)

- Acceleration is the gradient of the velocity-time graph.

- It has the same sinusoidal form as displacement but inverted as a=-ω²x.

- Acceleration is maximum at maximum displacement and zero at equilibrium as there is no restoring force acting there.

Draw and describe the graph of acceleration against time for a simple harmonic oscillator. (2)

- The graph should be sinusoidal and the time derivative of velocity, as a=dv/dt.

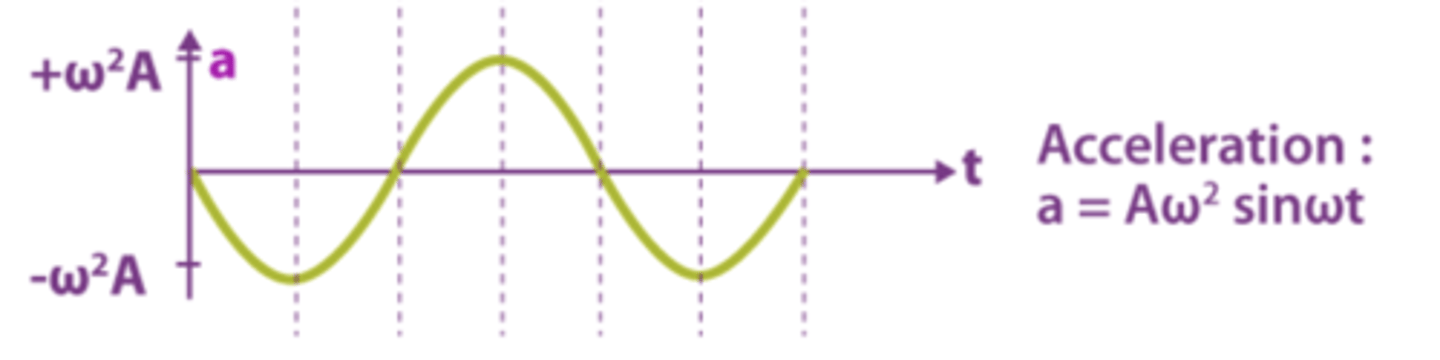
Draw the graphs of displacement, velocity and acceleration against time side by side for a simple harmonic oscillator. (3)

What are the energy transfers occurring during undamped, undriven simple harmonic motion? (2)

- Energy is periodically exchanged between potential and kinetic forms.

- The total energy in the system remains constant as none is lost to damping forces or provided by driving forces.

When are the kinetic and potential energies maximum in SHM? (4)

- Kinetic energy is maximum at equilibrium.

- This is because kinetic energy is proportional to velocity squared: Ek=1/2mv², so is maximum when velocity is maximum.

- Potential energy is maximum at amplitude.

- This is because potential energy is proportional to displacement, and displacement is maximum at amplitude.

What are the forms of energy present in a mass-spring system in comparison to a pendulum system? (2)

- Both have conversions between kinetic and potential energies.

- In a mass-spring system, the potential energy is elastic potential whereas in a pendulum system, the potential energy is gravitational potential.

How would you calculate the kinetic energy of a mass-spring system at displacement x? (4)

- The total energy is the sum of kinetic and potential energies, and we know that the total energy is the elastic potential at amplitude.

- Therefore we can write Etot=1/2kA².

- The kinetic energy is the difference ebtweem the total energy and the potential energy at displacement x.

- Therefore we can write Ek=1/2kA²-1/2kx² or Ek=1/2k(A²-x²).

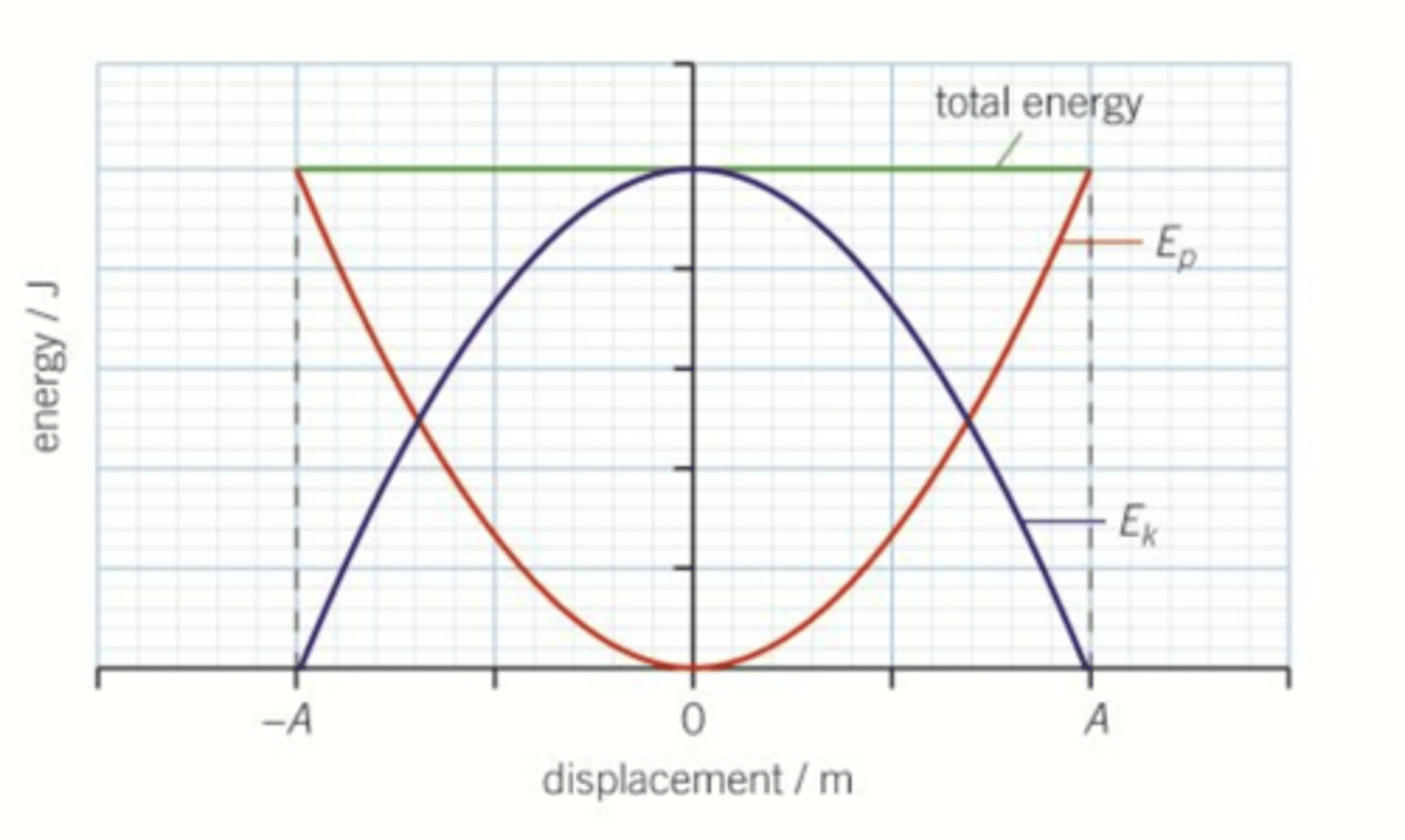
Draw and describe the graphs of kinetic, potential and total energy against displacement for a simple harmonic oscillator. (3)

- Total energy is a constant straight line.

- Ep is a quadratic with a minimum at equilibrium.

- Ek is a quadratic with a maximum at equilibrium.

What energy changes occur for the motion of a mass on a spring freely oscillating due to its weight? (4)

- The equilibrium position lies below the natural length of the spring due to weight of mass causing extension.

- At the lowest point in its motion the mass has maximum elastic potential energy.

- At equilibrium, the mass has maximum kinetic energy.

- At the highest point in its motion, the mass has maximum gravitational potential energy.

What is the difference between a free and a forced oscillation? (2)

- A free oscillation is the motion of a mechanical system which is displaced from its equilibrium position and allowed to oscillate without any external forces.

- A forced oscillation is an oscillation in which a periodic driver force is applied to the oscillator.

What is one example of a free oscillation and an example of a forced oscillation? (2)

- Examples of free oscillations include mass-spring systems or pendulums.

- Examples of forced oscillations include mass-spring systems attached to a vibration generator or a person on a swing.

What is the definition of damping? (1)

An oscillation is damped when an external force that acts on the oscillator has the effect of reducing the amplitude of its oscillations.

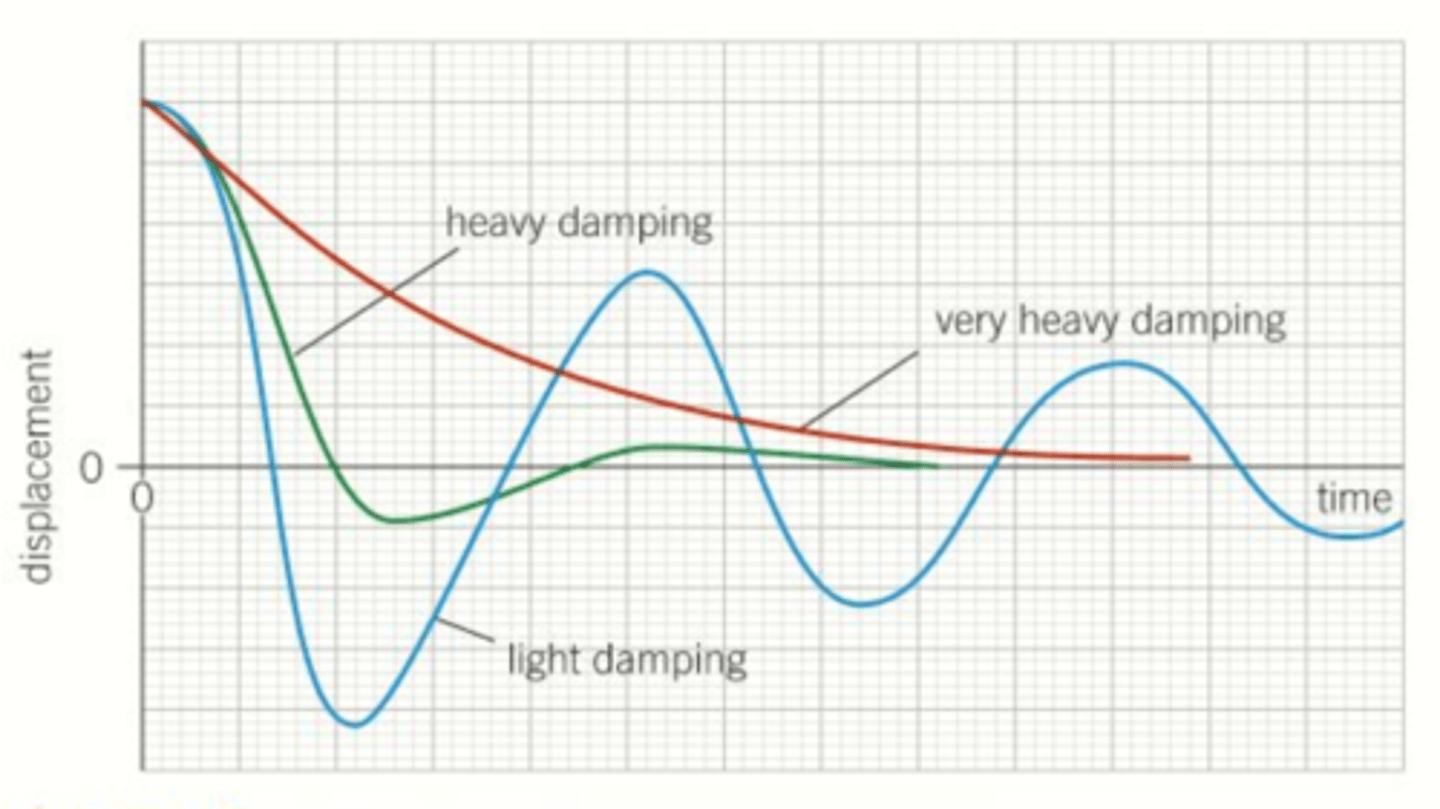
What are the different regimes of damping? (3)

- Light damping

- Heavy damping

- Very heavy damping.

What are the features of lightly damped oscillations? (3)

- The damping forces are small.

- The amplitude of oscillation decreases gradually with time.

- The period is unchanged.

What are the features of heavily damped oscillations? (3)

- The damping forces are large.

- The amplitude of oscillation decreases significantly and quickly.

- The period increases slightly.

What are the features of very heavily damped oscillations? (2)

- The damping is so large that there is no oscillation.

- Instead the system slowly returns to equilibrium.

What is an example of damping in a real world system? (2)

- Pendulum in air.

- The damping force is provided by air resistance which gradually reduces the amplitude of oscillation with time.

What are the features of the damping force acting on a pendulum oscillating in air? (3)

- The damping force is air resistance.

- The damping force is always opposite in direction to velocity.

- The damping force is maximum when displacement is zero.

Draw and describe the graph of displacement against time for a simple harmonic oscillator undergoing different types of damping. (3)

- Light damping shows a slow decrease in amplitude with time whereas heavy damping shows a faster decrease.

- In the very heavily damped case, there is no oscillation: the displacement never becomes negative and rather just decays exponentially with time.

What energy transfers occur during damped harmonic motion? (2)

- Energy is exchanged between kinetic and potential forms.

- Work is also done against the damping force meaning the total energy of the system is not constant.

What is the definition of resonance? (1)

Resonance is the increase in amplitude of a forced oscillation when the driver frequency matches the natural frequency of the object.

What is the definition of natural frequency? (1)

The natural frequency, f0 is the frequency of a free oscillation.

What is the condition for resonance? (1)

Resonance occurs when the frequency of the driving force matches the natural frequency of the system.

Why does resonance cause maximum amplitude? (2)

- Resonance causes maximum amplitude because there is a maximum transfer of energy between the driver force and the oscillating system.

What happens to the resonance curve of an oscillating object as the amount of damping increases? (3)

- The amplitude at any frequency decreases.

- The maximum amplitude occurs at a frequency lower than f0.

- peak on amplitude-frequency graph becomes flatter and broader

Why does a glass shatter when exposed to a sound at the natural frequency of the glass? (3)

- The glass resonates.

- The amplitude of the oscillations increases dramatically.

- Eventually the amplitude of the oscillations becomes so large that the glass breaks.

What are the useful effects of resonance? (3)

- In musical instruments, resonance is used to produce louder sounds.

- Resonance is useful in MRI machines (magnetic resonance imaging).

- Clocks use it to keep time using the resonance of a quartz crystal or pendulum.

Why can resonance be detrimental and how can this be rectified? (2)

- Resonance can cause structures to collapse. - This can be avoided by introducing damping devices into structures in order to remove energy before the amplitude becomes too drastic.