Maths terms/ rules

a^m x aⁿ =

a^m+n

(a^m)ⁿ=

a^m×n

a^{−m =}

1/a^m

x^a/b =

(b√x)^a

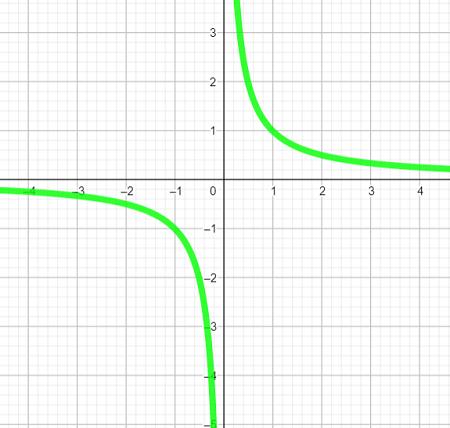
y = 1/x (as a graph)

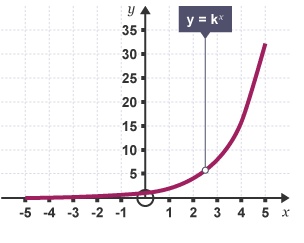
y = k^x (as a graph)

describe a cosine graph

• repeats every 360*

• goes through (0,1)

• goes through (90,0)

describe a sine graph.

• repeats every 360*

• goes through (0,0)

• goes through (90,1)

describe a tangent graph

• repeats every 180*

• never hits 90*

y = f(x+a) how does it transform a graph?

translates   a    units left

y = f(x)+a   how does it transform a graph?

translates a units up

y =-f(x) how does it transform a graph?

reflects in the x axis(verticle)

y = f(-x) how does it transform a graph?

reflects in the y axis (horizontal)

what is sin: 0, 30, 45, 60, 90

• sin(0) = 0

• sin(30) =1/2

• sin(45) = √2/2

• sin(60) =√3/2

• sin(90) = 1

what is cosine: 0, 30, 45, 60, 90

• cosine(0) = 1

• cosine(30) = √3/2

• cosine(45) = √2/2

• cosine(60) = 1/2

• cosine(90) = 0

what is tan: 0, 30, 45, 60

• tan(0) = 0

• tan(30) = 1/√3

• tan(45) = 1

• tan(60) = √3

y^{a/b =}

^b√y^a

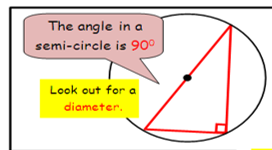
circle theorem semi circle rule:

angle of a semi cricle is 90*

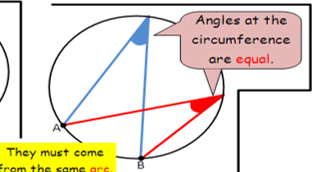
circle theorem angles at circumference:

angles at the circumference are equal if they are from the same arc

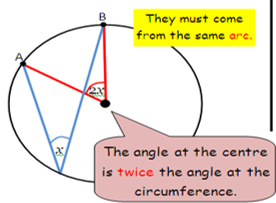
circle theorem angles at the centre:

angles at the centre are twice the angle at the circumference if they are from the same arc.

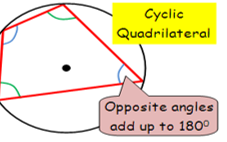
circle theorems cyclic quadrilateral: 

opposite angles add up to 180*

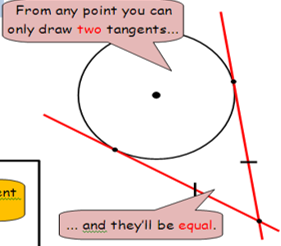
circle theorems if you draw two tangents:

they will be equal

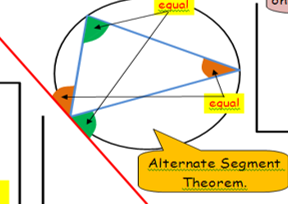
circle theorems alternate segment theorem.

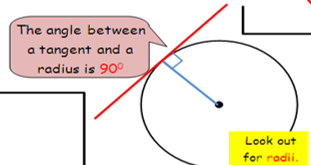
circle theorems how do the tangent and radius have a relationship

the angle between the tangent and radius is 90*

what are the different ways to prove congruence shapes?

SSS

SAS

ASA

RHS