fórmulas y teoría de matemáticas

Ángulo nulo

0

Ángulo agudo

0.1 a 89.9

Ángulo recto

90

ángulo obtuso

90.1 a 179.9

Ángulo llano

180

Angulo cóncavo

180.1 a 359.9

Ángulo completo

360

Ángulo complementario

Los dos suman exactamente, 90°

Ángulo suplementario

Los dos suman exactamente, 180°

Ángulo adyacente

Comparten un lado y un vértice formando un ángulo llano

Ángulo opuesto por el vértice

Se conforma de dos líneas cruzadas, siendo iguales entre sí

Ángulo consecutivo

Comparten en un lado y un vértice

Ángulo interior, polígono

Están dentro del polígono

Ángulo exterior

Está fuera del polígono

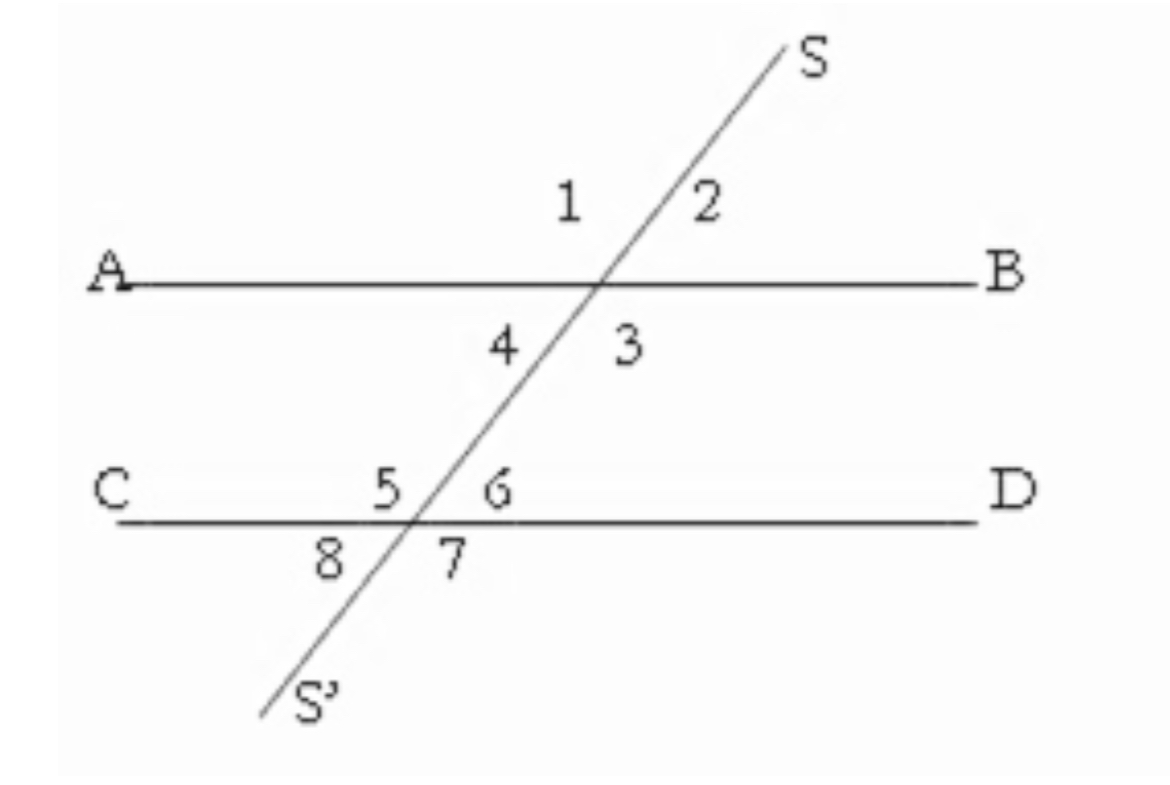
Ángulos externos

1,2,7,8

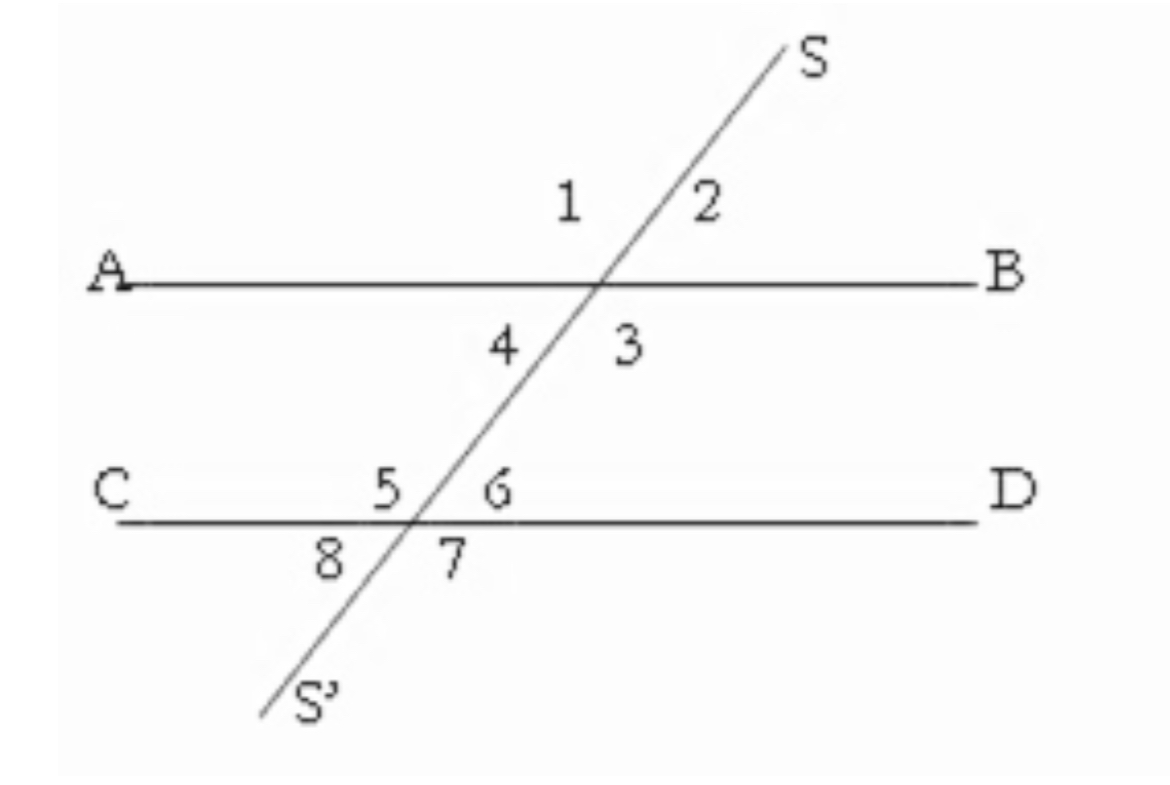
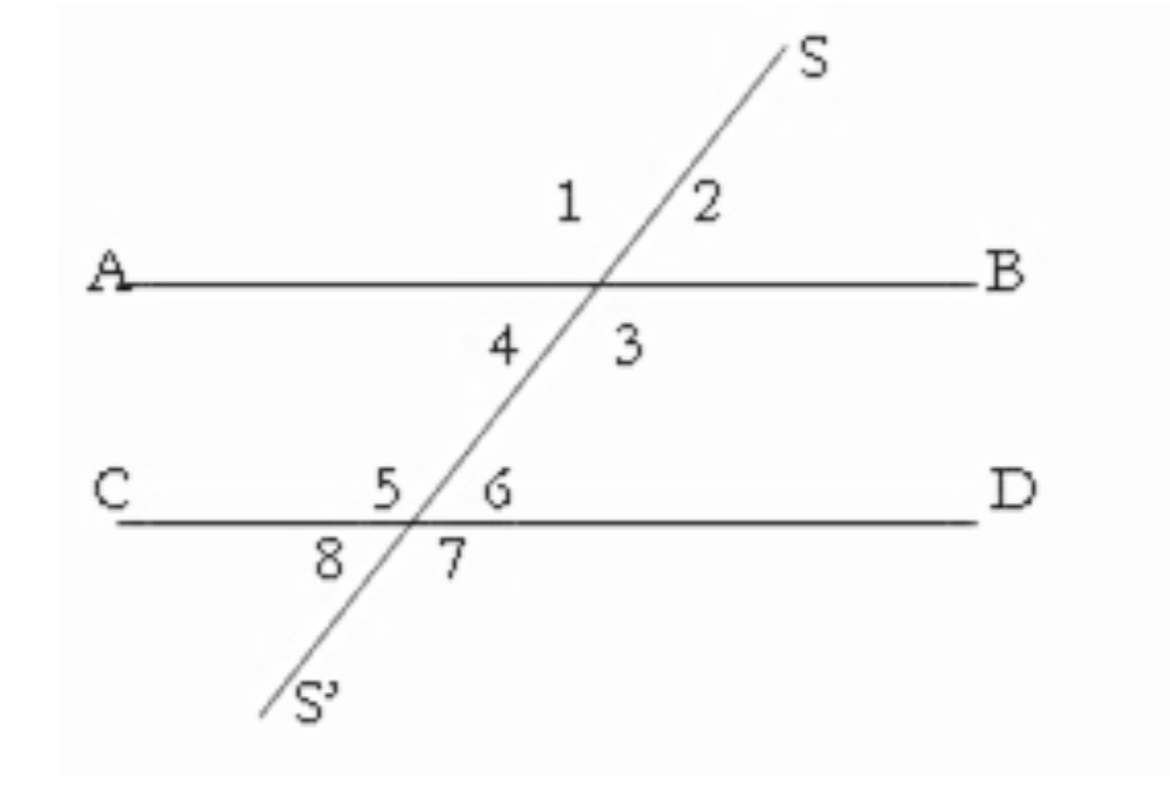
Ángulos alternos internos

3 y 5, 4 y 6

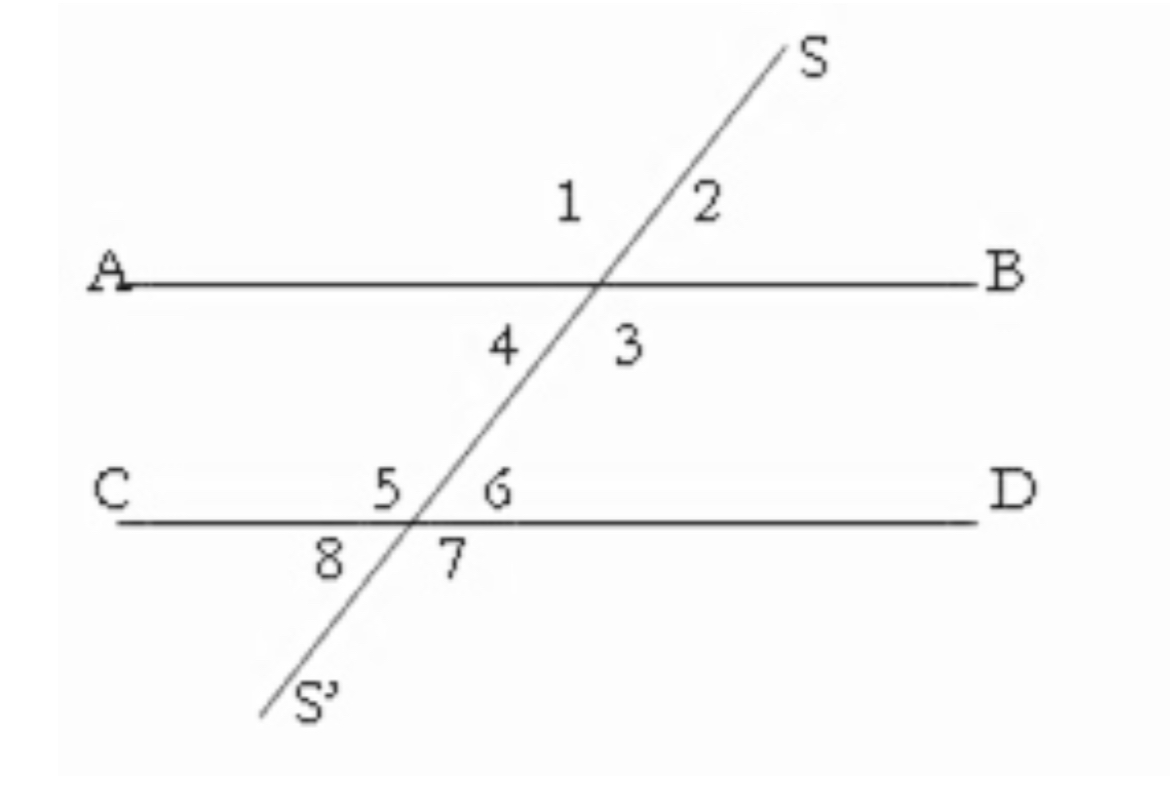
Ángulos alternos externos

1 y 7, 2 y 8

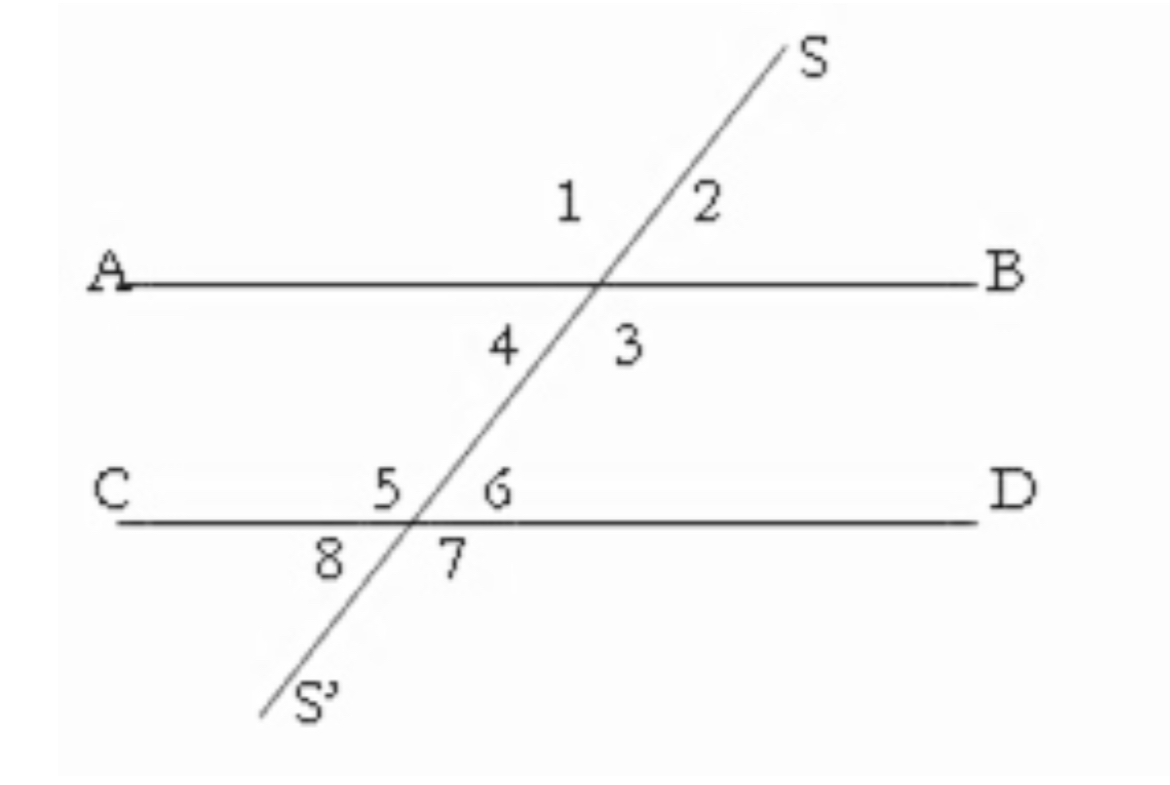
Ángulos correspondientes

1 y 5,2 y 6, 3 y 7, 4 y 8

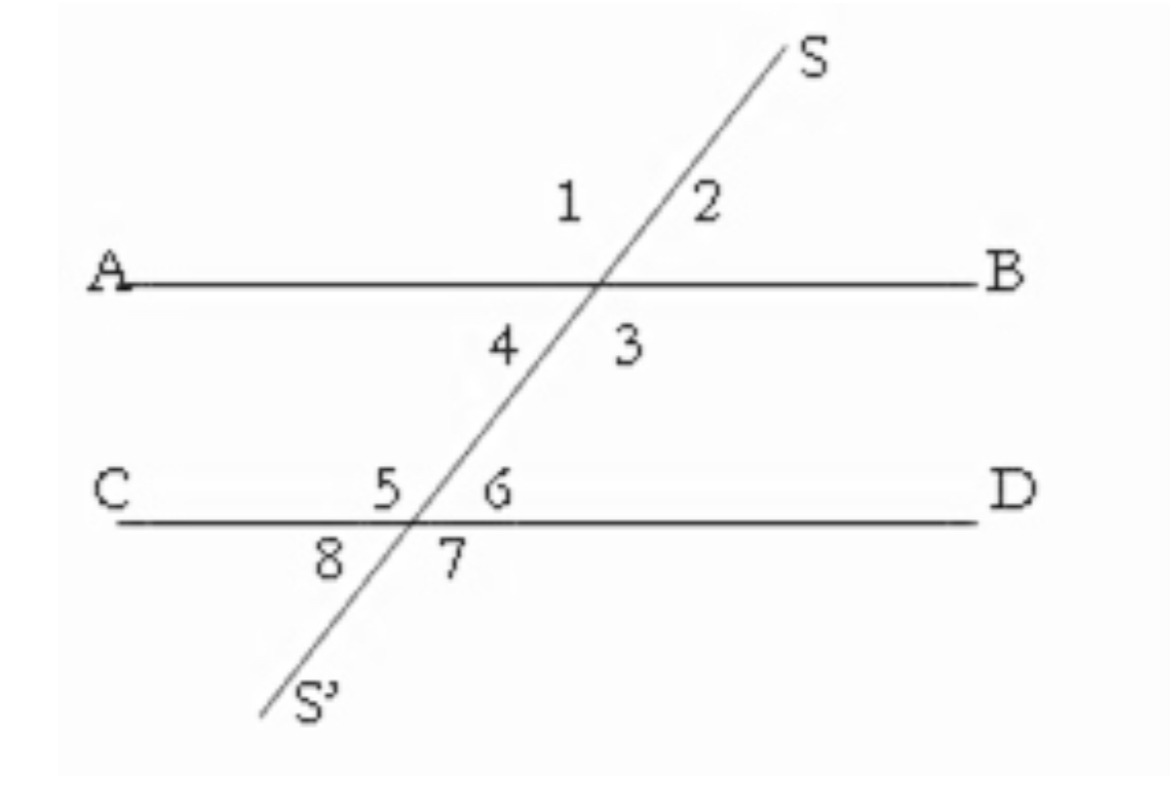
Ángulos colaterales internos

3 y 6, 4 y 5

Ángulos colaterales externos

1 y 8, 2 y 7

Fórmula general, de suma de ángulos en triángulos

A+B+C=180°

Triángulo equilátero

Todos sus lados son iguales

Triángulo isósceles

Sólo dos de sus ángulos son iguales

Triángulo Rectángulo

Uno de sus ángulos mide 90°, y los otros dos ángulos suman 90

Triángulo obtusángulo

Tiene un ángulo mayor a 90° y sus otros dos ángulos suman menos de 90

Qué es un polígono regular?

Aquel que tiene todos sus lados y ángulos iguales

Fórmula para suma de Los ángulos interiores de un polígono

S = (n - 2) × 180°

Fórmula para sacar la medida de el ángulo interior de un polígono

Ai = (n - 2) × 180°

---

2

Fórmula para sacar los ángulos exteriores de un polígono regular

Ai= 360 / n

Ángulos correspondientes congruentes

ángulos de un triángulo son iguales a los ángulos del otro triángulo

Lados correspondientes proporcionales

lados de un triángulo son proporcionales a los lados del otro triángulo. Es decir, la razón de los lados correspondientes es constante

AA (Ángulo-Ángulo)

Si dos ángulos de un triángulo son iguales a dos ángulos de otro triángulo, los triángulos son semejantes

LAL (Lado-Ángulo-Lado)

Si un lado de un triángulo es proporcional al lado correspondiente de otro triángulo, y los ángulos comprendidos entre esos lados son congruentes, entonces los triángulos son semejantes

LLL (Lado-Lado-Lado)

Si los tres lados de un triángulo son proporcionales a los tres lados correspondientes de otro triángulo, los triángulos son semejantes

Proporción de lados de dos triángulos semejantes

AB = BC = CA

— — —-

DE EF DF

congruencia de triángulos

propiedad geométrica que establece que dos triángulos son congruentes si tienen la misma forma y el mismo tamaño, es decir, si todos sus lados y todos sus ángulos correspondientes son exactamente iguales.

LLL (Lado-Lado-Lado)

tres lados correspondientes son iguales.

LAL (Lado-Ángulo-Lado)

Dos lados y el ángulo comprendido entre ellos son iguales.

AAL (Ángulo-Ángulo-Lado)

Dos ángulos y un lado no comprendido entre ellos son iguales.

ALA (Ángulo-Lado-Ángulo)

Un ángulo y los dos lados que lo contienen son iguales.

LLA (Lado-Lado-Ángulo)

Dos lados y un ángulo no comprendido entre ellos son iguales.

¿Qué es una razón trigonométrica?

Es el cociente entre dos lados de un triángulo rectángulo.

¿Qué es el seno (sen)?

sen(\theta) = \frac{\text{cateto opuesto}}{\text{hipotenusa}}

¿Qué es el coseno (cos)?

cos(\theta) = \frac{\text{cateto adyacente}}{\text{hipotenusa}}

¿Qué es la tangente (tan)?

tan(\theta) = \frac{\text{cateto opuesto}}{\text{cateto adyacente}}

¿Qué es la cotangente (cot)?

cot(\theta) = \frac{\text{cateto adyacente}}{\text{cateto opuesto}}

¿Qué es la secante (sec)?

sec(\theta) = \frac{\text{hipotenusa}}{\text{cateto adyacente}}

¿Qué es la cosecante (csc)?

csc(\theta) = \frac{\text{hipotenusa}}{\text{cateto opuesto}}

¿Qué dice el Teorema de Pitágoras?

En un triángulo rectángulo:
c^2 = a^2 + b^2
(c = hipotenusa, a y b = catetos)

¿Cuándo se usa el Teorema de Pitágoras?

Cuando se conocen dos lados y se quiere hallar el tercero en un triángulo rectángulo.

¿Qué dice la Ley de Senos?

\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
(a, b, c = lados; A, B, C = ángulos opuestos)

¿Cuándo se usa la Ley de Senos?

En triángulos no rectángulos, cuando conoces:

• AAS (ángulo, ángulo, lado)
• ASA (ángulo, lado, ángulo)
• SSA (lado, lado, ángulo no comprendido)

¿Qué dice la Ley de Cosenos?

c^2 = a^2 + b^2 - 2ab \cdot \cos(C)

¿Cuándo se usa la Ley de Cosenos?

En triángulos no rectángulos, en los casos:

• Lado, Ángulo, Lado (LAL)
• Lado, Lado, Lado (LLL)

¿Qué es la geometría euclidiana?

Geometría tradicional basada en los postulados de Euclides, usada en espacios planos.

Postulado de las paralelas (Euclides):

Dado un punto fuera de una recta, existe una única recta paralela que pasa por ese punto.

¿Cuánto suman los ángulos de un triángulo euclidiano?

Siempre suman 180^{\circ}

¿Qué es la geometría hiperbólica?

Existen infinitas paralelas por un punto externo. Espacio con curvatura negativa.

¿Qué es la geometría elíptica?

No hay paralelas. Todas las líneas se cruzan. Espacio con curvatura positiva.

¿En qué se usa la geometría no euclidiana?

En física, relatividad, y modelos del universo curvo.

¿Cuánto suman los ángulos en un triángulo hiperbólico?

Menos de 180^{\circ}

¿Cuánto suman los ángulos en un triángulo elíptico?

Más de 180^{\circ}

¿Qué es una circunferencia unitaria?

Es una circunferencia de radio 1. Sirve para extender funciones trigonométricas.

¿Qué es un triángulo oblicuángulo?

Triángulo que no tiene ángulo recto.

¿Qué significa “ángulo de elevación”?

Es el ángulo que se forma al mirar hacia arriba desde el horizonte.

¿Qué significa “ángulo de depresión”?

Es el ángulo al mirar hacia abajo desde una línea horizontal.

¿Qué es una razón trigonométrica?

Es el cociente entre dos lados de un triángulo rectángulo.

¿Qué es el seno (sen)?

sen(\theta) = \frac{\text{cateto opuesto}}{\text{hipotenusa}}

¿Qué es el coseno (cos)?

cos(\theta) = \frac{\text{cateto adyacente}}{\text{hipotenusa}}

¿Qué es la tangente (tan)?

tan(\theta) = \frac{\text{cateto opuesto}}{\text{cateto adyacente}}

¿Qué es la cotangente (cot)?

cot(\theta) = \frac{\text{cateto adyacente}}{\text{cateto opuesto}}

¿Qué es la secante (sec)?

sec(\theta) = \frac{\text{hipotenusa}}{\text{cateto adyacente}}

¿Qué es la cosecante (csc)?

csc(\theta) = \frac{\text{hipotenusa}}{\text{cateto opuesto}}

¿Qué dice el Teorema de Pitágoras?

En un triángulo rectángulo:
c^2 = a^2 + b^2
(c = hipotenusa, a y b = catetos)

¿Cuándo se usa el Teorema de Pitágoras?

Cuando se conocen dos lados y se quiere hallar el tercero en un triángulo rectángulo.

¿Qué dice la Ley de Senos?

\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
(a, b, c = lados; A, B, C = ángulos opuestos)

¿Cuándo se usa la Ley de Senos?

En triángulos no rectángulos, cuando conoces:

• AAS (ángulo, ángulo, lado)
• ASA (ángulo, lado, ángulo)
• SSA (lado, lado, ángulo no comprendido)

¿Qué dice la Ley de Cosenos?

c^2 = a^2 + b^2 - 2ab \cdot \cos(C)

¿Cuándo se usa la Ley de Cosenos?

En triángulos no rectángulos, en los casos:

• Lado, Ángulo, Lado (LAL)
• Lado, Lado, Lado (LLL)

¿Qué es la geometría euclidiana?

Geometría tradicional basada en los postulados de Euclides, usada en espacios planos.

Postulado de las paralelas (Euclides):

Dado un punto fuera de una recta, existe una única recta paralela que pasa por ese punto.

¿Cuánto suman los ángulos de un triángulo euclidiano?

Siempre suman 180^{\circ}

¿Qué es la geometría hiperbólica?

Existen infinitas paralelas por un punto externo. Espacio con curvatura negativa.

¿Qué es la geometría elíptica?

No hay paralelas. Todas las líneas se cruzan. Espacio con curvatura positiva.

¿En qué se usa la geometría no euclidiana?

En física, relatividad, y modelos del universo curvo.

¿Cuánto suman los ángulos en un triángulo hiperbólico?

Menos de 180^{\circ}

¿Cuánto suman los ángulos en un triángulo elíptico?

Más de 180^{\circ}

¿Qué es una circunferencia unitaria?

Es una circunferencia de radio 1. Sirve para extender funciones trigonométricas.

¿Qué es un triángulo oblicuángulo?

Triángulo que no tiene ángulo recto.

¿Qué significa “ángulo de elevación”?

Es el ángulo que se forma al mirar hacia arriba desde el horizonte.

¿Qué significa “ángulo de depresión”?

Es el ángulo al mirar hacia abajo desde una línea horizontal.

¿Qué es una razón trigonométrica?

Una razón trigonométrica es el cociente entre dos lados de un triángulo rectángulo respecto a uno de sus ángulos agudos.

¿Qué es el seno? (sen θ)

\sin \theta = \frac{\text{cateto opuesto}}{\text{hipotenusa}}

¿Qué es el coseno? (cos θ)

\cos \theta = \frac{\text{cateto adyacente}}{\text{hipotenusa}}

¿Qué es la tangente? (tan θ)

\tan \theta = \frac{\text{cateto opuesto}}{\text{cateto adyacente}}

¿Qué es la cotangente? (cot θ)

\cot \theta = \frac{\text{cateto adyacente}}{\text{cateto opuesto}}

¿Qué es la secante? (sec θ)

\sec \theta = \frac{\text{hipotenusa}}{\text{cateto adyacente}}

¿Qué es la cosecante? (csc θ)

\csc \theta = \frac{\text{hipotenusa}}{\text{cateto opuesto}}

¿Qué establece el Teorema de Pitágoras?

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos:
c^2 = a^2 + b^2