Simple graph theory concepts

graph

a collection of points called vertices or nodes and line segments or curves called edges that connect the vertices.

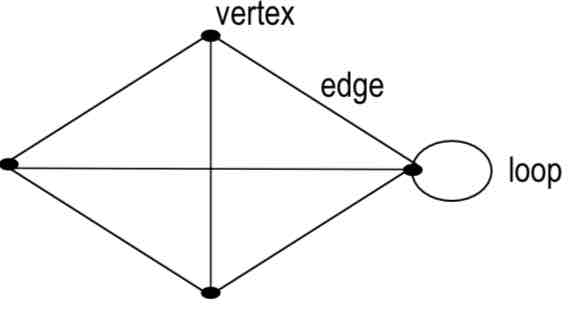
vertices/nodes

collection of points

edges

line segments or curves

loop

an edge connecting a vertex to itself.

complete graph

a graph that has an edge connecting every pair of vertices.

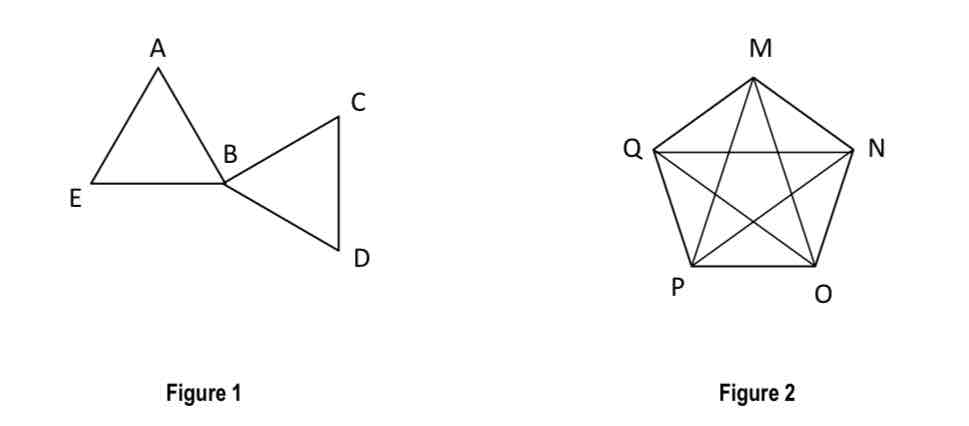
adjacent

there is an edge joining them.

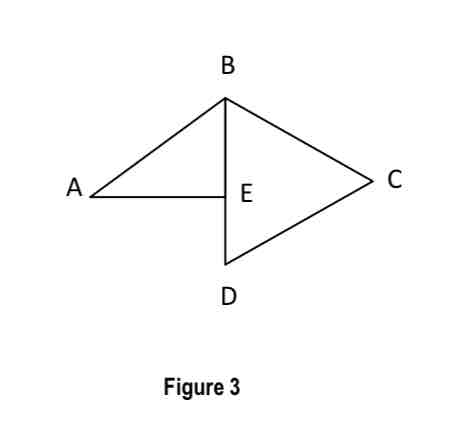
equivalent

same vertices connected in the same way.

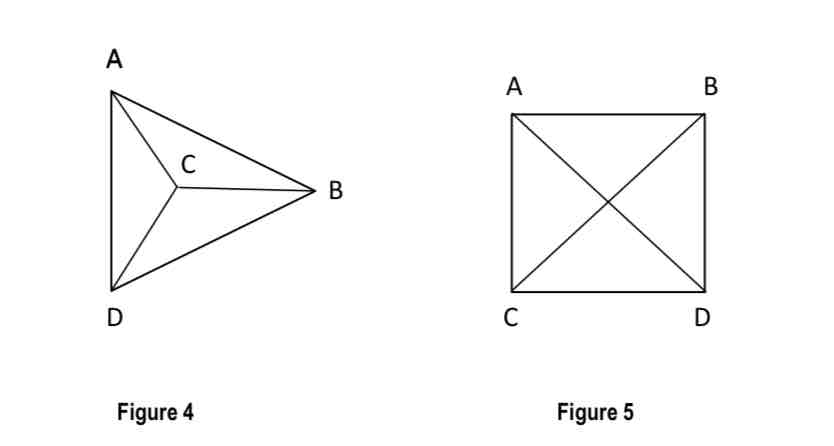
path

alternating sequence of vertices and edges.

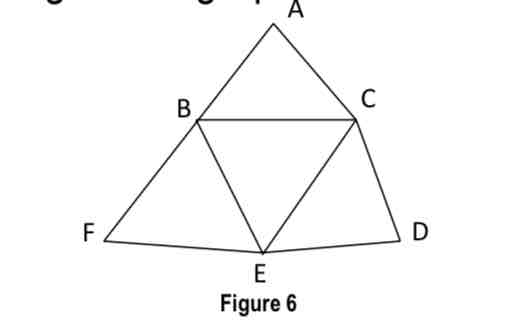
circuit

a path that begins and ends with the same vertex

A graph is ______ if for any two vertices, there is at

least one path that joins them.

connected

bridge

edge that when you remove makes the graph disconnected.

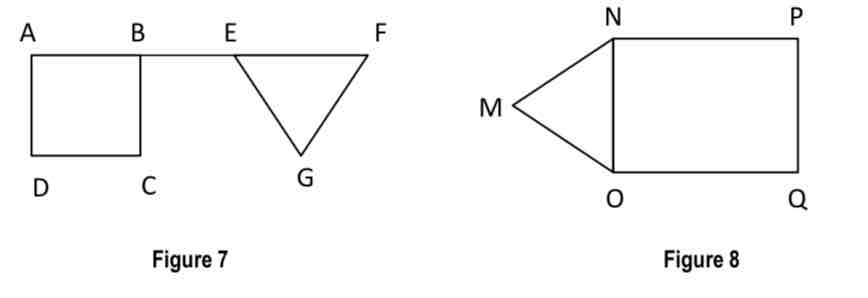
degree

the number of edges attached to a vertex

graph coloring

The idea is to color the vertices or edges of a graph in such a way that adjacent vertices or concurrent edges are given different colors.

chromatic number of the graph

The smallest number of colors required to color the vertices of a graph

2- Colorable Graph Theorem

A graph is 2-colorable if and only if it has no circuits that consist of odd number of vertices.

Four-Color Theorem

The chromatic number of a planar graph is at most 4.

adjacent

if they share part of their boundaries.

Euler path

• a path that passes through every edge exactly once only

• a path that contains all the edges of the graph

• begin and end with the odd-degree vertices

• if and only if no more than two of its vertices have odd degree.

Euler circuit

a closed path that contains all the edges of the graph.

Eulerian

A graph that has an Euler circuit

A ____ is Eulerian if and only if each vertex

has even degree.

Connected graph

if all vertices are ______ the graph has at least one Euler

circuit

even

exactly two vertices are ___, the graph has no Euler circuits but at least one Euler path.

odd

If there are more than ___ vertices, the graph

has no Euler path and no Euler circuits.

two odd

Hamiltonian path

a path passing through each vertex of the graph exactly once.

Hamiltonian cycle

If the hamiltonian path is closed

Hamiltonian

If a graph has a Hamiltonian cycle, it is called Hamiltonian.

tree

a graph in which any two vertices are connected by exactly one path.

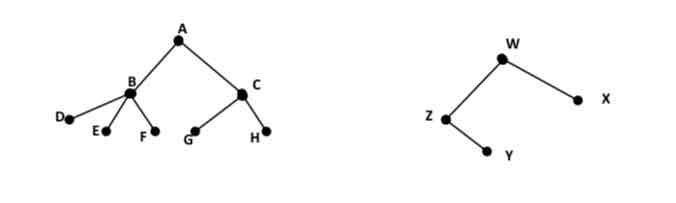
forest

an undirected, disconnected, acyclic graph. In other words, a disjoint collection of trees is known as forest.

spanning tree

a tree that results from the removal of as many edges as possible from the original graph without making it disconnected.

minimum spanning tree

• the spanning tree for the graph that has the smallest possible sum of the weights.

• must have one fewer edge than the number of vertices.

Prim's algorithm

a minimum spanning tree algorithm that takes a graph as input and finds the subset of the edges of that graph which

1. form a tree that includes every vertex

2. has the minimum sum of weights among all the trees that can be formed from the graph