Mini Project #3

Area of a Triangle using Angle

Formula: A = ½absin(C)

Topic: Geometry and Trigonometry

Subtopic: SL 3.2

Area of a Circle

Formula: A = π.r²

Topic: Prior Learning

Circumference of a Circle

Formula: C = 2π.r

Topic: Prior Learning

Volume of a Cuboid

Formula: V = lwh

Topic: Prior Learning

Volume of a Cylinder

Formula: V = π.r²h

Topic: Prior Learning

Volume of a Prism

Formula: V = Ah

Topic: Prior Learning

Area of the curved surface of a Cylinder

Formula: A = 2π.rh

Topic: Prior Learning

Distance between two points formula 2D

Formula: d = √'(x1 - x2)² + (y1 - y2)²

Topic: Prior Learning

Midpoint formula 2D

Formula: m = ((x1 + x2)/2, (y1 + y2)/2)

Topic: Prior Learning

Distance Formula between 2 Points 3D

Formula: d = √'(x1 - x2)² + (y1 - y2)² + (z1 - z2)²

Topic: Geometry and Trigonometry

Subtopic: SL 3.1

Midpoint formula 3D

Formula: m = ((x1 + x2)/2, (y1 + y2)/2, (z1 + z2)/2)

Topic: Geometry and Trigonometry

Subtopic: SL 3.1

Volume of a right pyramid

Formula: V = 1/3Ah

Topic: Geometry and Trigonometry

Subtopic: SL 3.1

Volume of a right cone

Formula: V = 1/3π.r²h

Topic: Geometry and Trigonometry

Subtopic: SL 3.1

Area of the curved surface of a cone

Formula: A = π.rl

Topic: Geometry and Trigonometry

Subtopic: SL 3.1

Volume of a Sphere

Formula: V = 4/3π.r³

Topic: Geometry and Trigonometry

Subtopic: SL 3.1

Surface area of a sphere

Formula: A = 4π.r²

Topic: Geometry and Trigonometry

Subtopic: SL 3.1

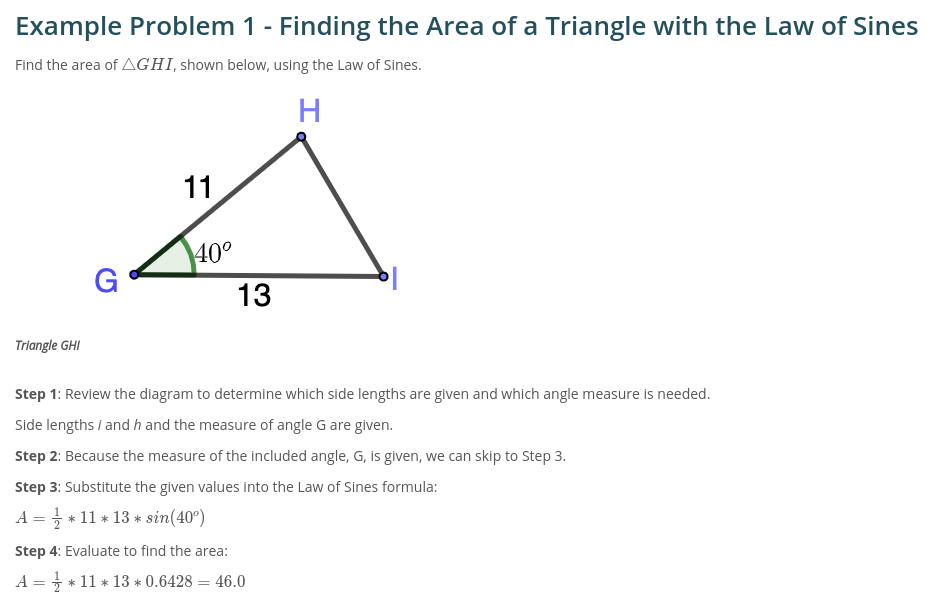
Area using law of sines

Formula: A = ½absin(C)

works when you have two angles and one side length

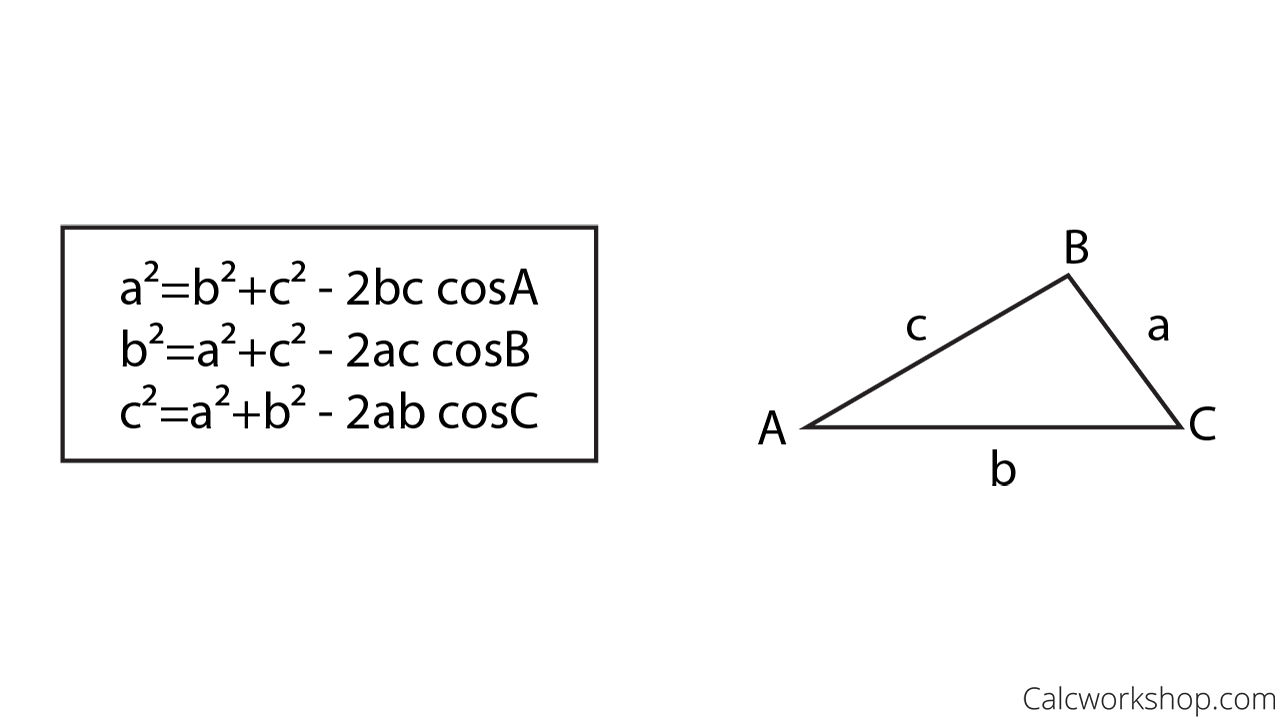
Area using law of cosines

Formula: c² = a² + b² - 2abcos(C) or cos(C) = (a² + b² - c²)/2ab

you would use this in order to find the 3rd side length of a triangle then you would use the area of a triangle formula in order to to find the area.

Finding an angle between two lines

In order to find an angle between two lines, you would first need to know the slopes of both lines so m1 and m2. Then you would use the Tangent function formula of: tan(theta) = (m2 - m1)/(1+ m1m2). For that solution, you would then make it theta = tan^-1 ((m2 - m1)/(1+ m1m2).)

How to represent 3 consecutive numbers

formula: n = any integer and to find a consecutive integer you would do n + 1, so n, n + 1, n + 2

How to represent an even number

2n

How to represent an odd number

(2n + 1)

How to represent 3 consecutive even numbers

2n, (2n + 2), (2n + 4)

How to represent 3 consecutive odd numbers

(2n + 1) (2n + 3) (2n + 5)

Number Theory proof example

Prove that the product between an odd and an even integer are always even:

2n(2n + 1) = 4n² + 2n →2(2n² + 1) Since any even integer is a multiple of two, it must be even.

Laws of logs Proof example