AP Calc AB Memorization Sheet

More terms added as we update the sheet in class

Sin(0)

0

Sin(π/6)

1/2

Sin(π/4)

√2/2

Sin(π/3)

√3/2

Sin(π/2)

1

Sin(π)

0

Sin(3π/2)

-1

Cos(0)

1

Cos(π/6)

√3/2

Cos(π/4)

√2/2

Cos(π/3)

1/2

Cos(π/2)

0

Cos(π)

-1

Cos(3π/2)

0

Tan(0)

0

Tan(π/6)

√3/3

Tan(π/4)

1

Tan(π/3)

√3

Tan(π/2)

UND

Tan(π)

0

Tan(3π/2)

UND.

Definition of a logarithm (the equation)

Log_ab=x and a^x=b

ln(e)=

1

ln(1)=

0

ln(MN)=

ln(M) + ln(N)

ln(M/N)=

ln(M) - ln(N)

p{ln(M)}

ln(M)^p

sin(-x)= ______ because it is ______

-sin(x), odd

cos(-x)= ______ because it is ______

cos(x), even

f(x)= x

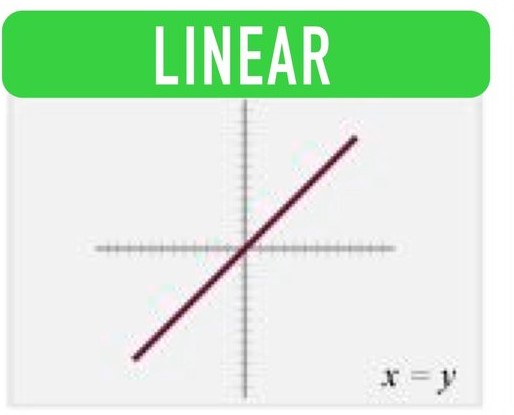
f(x)= x²

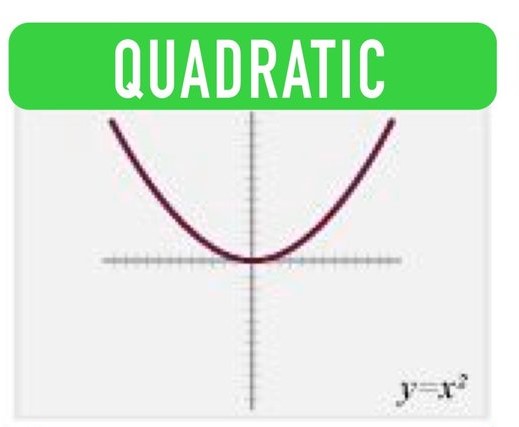
f(x)= x³

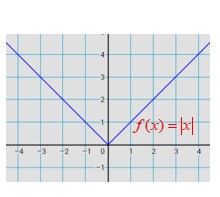
f(x)= IxI

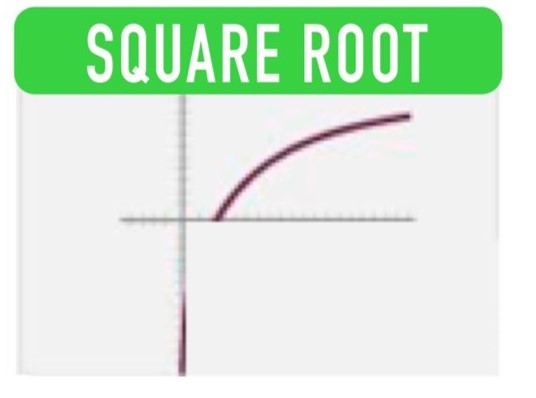
f(x)= √x

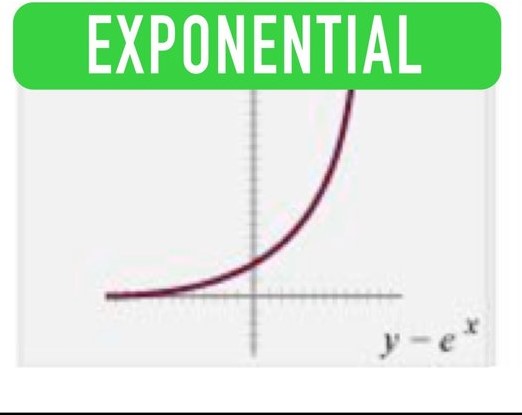
f(x)= e^x

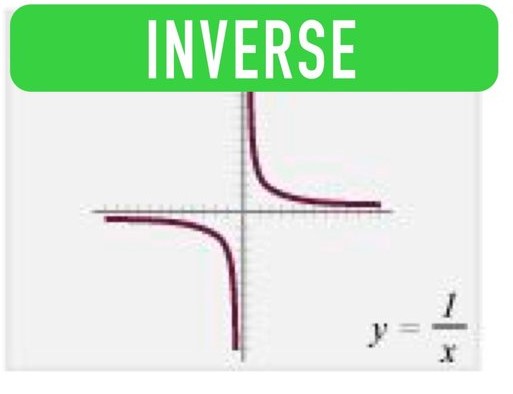
f(x)= 1/x

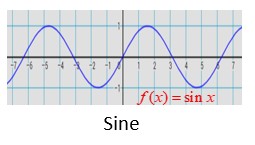
f(x)= sin(x)

f(x)= cos(x)

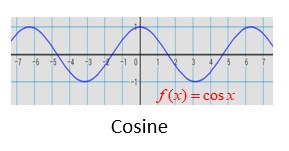
f(x)= Tan(x)

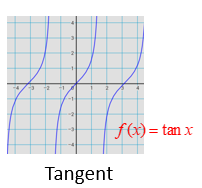
f(x)= ln(x)

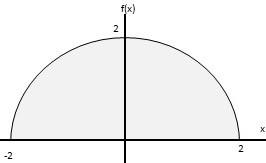
f(x)= √a²-x²

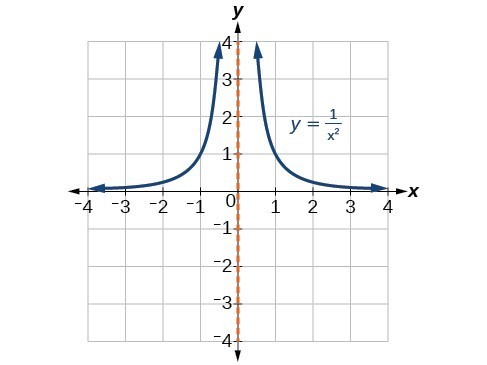
f(x)= 1/x²

3 Pythagorean Identities

1: Sin²x + Cos²x= 1

2: 1+ Tan²x= Sec²x

3: Cot²x + 1= Csc²x

2 Double Angle Formulas

Sin2x= 2(Cosx)(Sinx)

Cos2x= Cos²x- Sin²x = 1-Sin²x

Power-Reducing Formulas

Sin²x= 1/2( 1-2Cos2x)

Cos²x= 1/2( 1+2Cos2x)

Quotient Identities

Tan(x)= Sin(x)/Cos(x)

Cot(x)= 1/Tan(x)= Cos(x)/Sin(x)

Reciprocal Identities

Csc(x)= 1/sin(x)

Sec(x)= 1/cos(x)

(d/dx)(xⁿ)=

n(x^n-1)

(d/dx)(sinx)=

cosx

(d/dx)(cosx)=

-sinx

(d/dx)(tanx)=

sec²x

(d/dx)(cotx)=

-csc²x

(d/dx)(secx)=

(secx)(tanx)

(d/dx)(cscx)=

(-cscx)(cotx)

(d/dx)(lnu)=

1/u

(d/dx)(e^u)=

e^u

(d/dx)(a^x)=

(a^x)lna

(d/dx)(log_ax)=

{1/lna(x)}

f(x) is continuous at point c iff:

1: f( c ) is defined

2: lim_x→c f(x) exists

3: lim_x→c f(x)=f( c )

Degree(denominator) > degree(numerator):

lim_x→±∞ f(x)=0

Degree(denominator) < Degree(numerator):

lim_x→±∞ f(x)=DNE

Degree(denominator) = Degree(numerator):

lim_x→±∞ f(x)= Ratio of Leading Coefficients

There is a vertical asymptote at c iff

a one sided limit is ±∞

Instantaneous Rate of Change:

f’(x)=lim_h→0 f(x+h)-f(x)/h

Average Rate of Change:

f(b)-f(a)/b-a

Equation of a Tangent Line: You need a ____ and a _____

point, slope/derivative of the x-value

What is the Equation of a Tangent Line?

y-y₁= f’(x₁)(x-x₁)

Derivative at a Point c:

f’( c)_x→c f(x)-f(c )/x-c

Product Rule: (d/dx)(uv)=

u(v’)+ v(u’)

Quotient Rule: (d/dx)(u/v)=

v(u’)-u(v’)/v²

Intermediate Value Theorem: if f(x) is ________ and ________ then ________

is continous on [a&b}, and k is between f(b) & f(a), then there is a c in [a,b] such that f(c )=K